
Question and Answers Forum
Question Number 111762 by mathmax by abdo last updated on 04/Sep/20
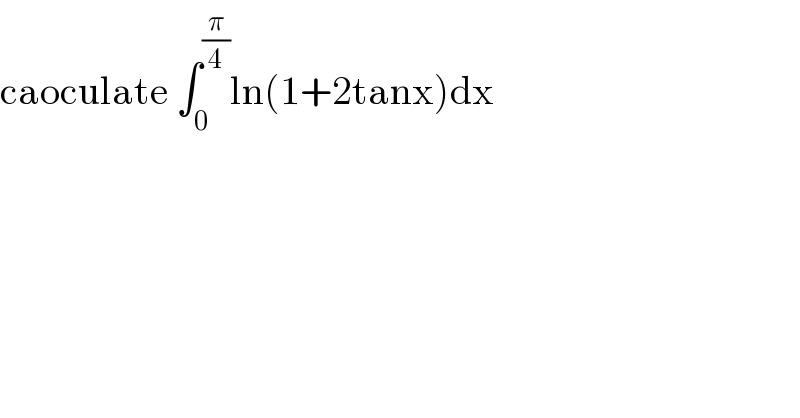
Answered by mathmax by abdo last updated on 12/Sep/20
![A =∫_0 ^(π/4) ln(1+2tanx)dx let f(a) =∫_0 ^(π/4) ln(1+atanx)dx witha>0 f^′ (a) =∫_0 ^(π/4) ((tanx)/(1+atanx)) dx =_(tanx =t) ∫_0 ^1 (t/((1+at)(1+t^2 ))) dt let decompose u(t) =(t/((at+1)(t^2 +1))) ⇒u(t) =(α/(at +1)) +((βt +λ)/(t^(2 ) +1)) α =((−1)/(a((1/a^2 )+1))) =((−a^2 )/(a(1+a^2 ))) =−(a/(a^2 +1)) lim_(t→+∞) tu(t) =0 =(α/a) +β ⇒β =(1/(a^2 +1)) u(0) =0 =α +λ ⇒λ =(a/(a^2 +1)) ⇒u(t) =−(a/((a^2 +1)(at+1))) +(((t/(a^2 +1))+(a/(a^2 +1)))/(t^2 +1)) ⇒f^′ (a) =−(a/(a^2 +1))∫_0 ^1 (dt/(at +1)) +(1/(a^2 +1))∫_0 ^1 ((t+a)/(t^2 +1)) dt =−(1/(a^2 +1))[ln(at+1)]_0 ^1 +(1/(2(a^2 +1))) ∫_0 ^1 ((2t)/(1+t^2 ))dt +(a/(a^2 +1))[arctant]_0 ^1 =−((ln(a+1))/(a^2 +1))+((ln(2))/(2(a^2 +1))) +((πa)/(4(a^2 +1))) ⇒ f(a)=−∫_0 ^a ((ln(1+x))/(1+x^2 )) dx +((ln2)/2) ∫_0 ^a (dx/(1+x^2 )) +(π/4) ∫_0 ^a (x/(1+x^2 )) dx +c =−∫_0 ^a ((ln(1+x))/(1+x^2 ))dx +((ln2)/2) arctan(a) +(π/8)ln(1+a^2 ) +c c=f(0) =0 and A =f(2) =−∫_0 ^2 ((ln(1+x))/(1+x^2 ))dx+((ln2)/2) arctan2+(π/8)ln5 rest calculus of ∫_0 ^2 ((ln(1+x))/(1+x^2 )) dx....be continued...](Q113335.png)
| ||
Question and Answers Forum | ||
Question Number 111762 by mathmax by abdo last updated on 04/Sep/20 | ||
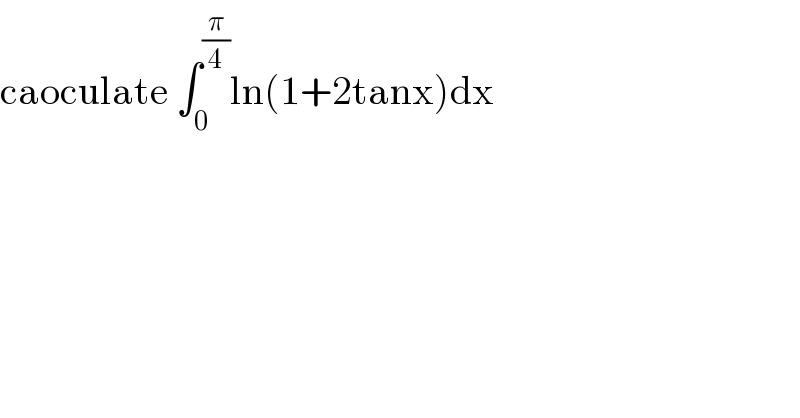 | ||
Answered by mathmax by abdo last updated on 12/Sep/20 | ||
![A =∫_0 ^(π/4) ln(1+2tanx)dx let f(a) =∫_0 ^(π/4) ln(1+atanx)dx witha>0 f^′ (a) =∫_0 ^(π/4) ((tanx)/(1+atanx)) dx =_(tanx =t) ∫_0 ^1 (t/((1+at)(1+t^2 ))) dt let decompose u(t) =(t/((at+1)(t^2 +1))) ⇒u(t) =(α/(at +1)) +((βt +λ)/(t^(2 ) +1)) α =((−1)/(a((1/a^2 )+1))) =((−a^2 )/(a(1+a^2 ))) =−(a/(a^2 +1)) lim_(t→+∞) tu(t) =0 =(α/a) +β ⇒β =(1/(a^2 +1)) u(0) =0 =α +λ ⇒λ =(a/(a^2 +1)) ⇒u(t) =−(a/((a^2 +1)(at+1))) +(((t/(a^2 +1))+(a/(a^2 +1)))/(t^2 +1)) ⇒f^′ (a) =−(a/(a^2 +1))∫_0 ^1 (dt/(at +1)) +(1/(a^2 +1))∫_0 ^1 ((t+a)/(t^2 +1)) dt =−(1/(a^2 +1))[ln(at+1)]_0 ^1 +(1/(2(a^2 +1))) ∫_0 ^1 ((2t)/(1+t^2 ))dt +(a/(a^2 +1))[arctant]_0 ^1 =−((ln(a+1))/(a^2 +1))+((ln(2))/(2(a^2 +1))) +((πa)/(4(a^2 +1))) ⇒ f(a)=−∫_0 ^a ((ln(1+x))/(1+x^2 )) dx +((ln2)/2) ∫_0 ^a (dx/(1+x^2 )) +(π/4) ∫_0 ^a (x/(1+x^2 )) dx +c =−∫_0 ^a ((ln(1+x))/(1+x^2 ))dx +((ln2)/2) arctan(a) +(π/8)ln(1+a^2 ) +c c=f(0) =0 and A =f(2) =−∫_0 ^2 ((ln(1+x))/(1+x^2 ))dx+((ln2)/2) arctan2+(π/8)ln5 rest calculus of ∫_0 ^2 ((ln(1+x))/(1+x^2 )) dx....be continued...](Q113335.png) | ||
| ||