Proof for the following : n! ≥ 2×3^(n−2)


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 111954 by Hassen_Timol last updated on 05/Sep/20

$P roof for the following :$ $n! ⩾ 2 \times 3^{n - 2}$
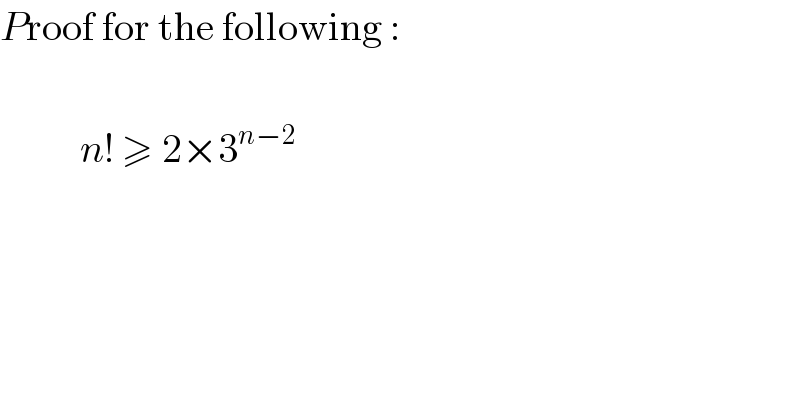
	Answered by mathmax by abdo last updated on 05/Sep/20
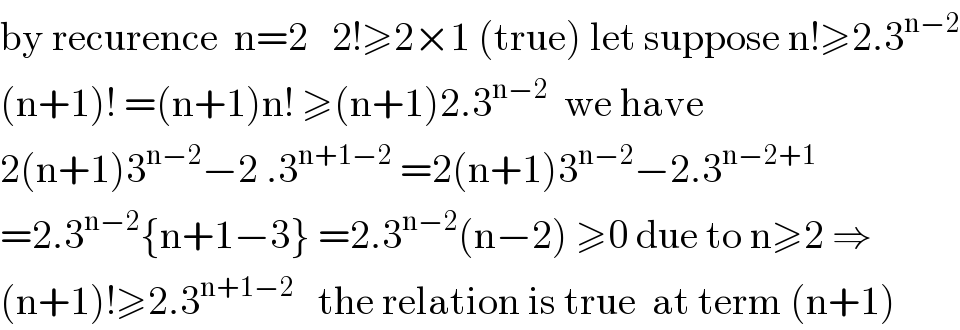
	$by recurence n=2 2!≥2×1 (true) let suppose n!≥2.3^(n−2) (n+1)! =(n+1)n! ≥(n+1)2.3^(n−2) we have 2(n+1)3^(n−2) −2 .3^(n+1−2) =2(n+1)3^(n−2) −2.3^(n−2+1) =2.3^(n−2) {n+1−3} =2.3^(n−2) (n−2) ≥0 due to n≥2 ⇒ (n+1)!≥2.3^(n+1−2) the relation is true at term (n+1)$
	$by recurence n = 2 2! ⩾ 2 \times 1 (true) let suppose n! ⩾ 2 . 3^{n - 2}$ $(n + 1)! = (n + 1) n! ⩾ (n + 1) 2 . 3^{n - 2} we have$ $2 (n + 1) 3^{n - 2} - 2 . 3^{n + 1 - 2} = 2 (n + 1) 3^{n - 2} - 2 . 3^{n - 2 + 1}$ $= 2 . 3^{n - 2} {n + 1 - 3} = 2 . 3^{n - 2} (n - 2) ⩾ 0 due to n ⩾ 2 \Rightarrow$ $(n + 1)! ⩾ 2 . 3^{n + 1 - 2} the relation is true at term (n + 1)$
	Commented by aleks041103 last updated on 05/Sep/20

	$H e u s e d p r o o f b y i n d u c t i o n$
	Commented by Hassen_Timol last updated on 05/Sep/20
	Sorry but I don't understand I think... ��
	Commented by mathmax by abdo last updated on 05/Sep/20

	$I have used recurrence method . . .$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum