....advanced calculus... evaluate: i:: ∫_0 ^( 1) xH_x dx =??? ii::Σ_(n=1 ) ^∞ (H_n /(n^2 2^(n ) )) =??? iii:: ∫_0 ^( 1) ((ln(((x+1))^(1/3) ))/((x+1)(x+2)))=??? m.n. july 1970...#


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 111965 by mnjuly1970 last updated on 05/Sep/20

$. . . . a d v a n c e d c a l c u l u s . . .$ $e v a l u a t e :$ $i :: \int_{0}^{1} {x H}_{x} d x = ? ? ?$ $i i :: \underset{n = 1}{\sum^{\infty}} \frac{H_{n}}{n^{2} 2^{n}} = ? ? ?$ $i i i :: \int_{0}^{1} \frac{l n (\sqrt[3]{x + 1})}{(x + 1) (x + 2)} = ? ? ?$ $You can't use 'macro parameter character #' in math mode$
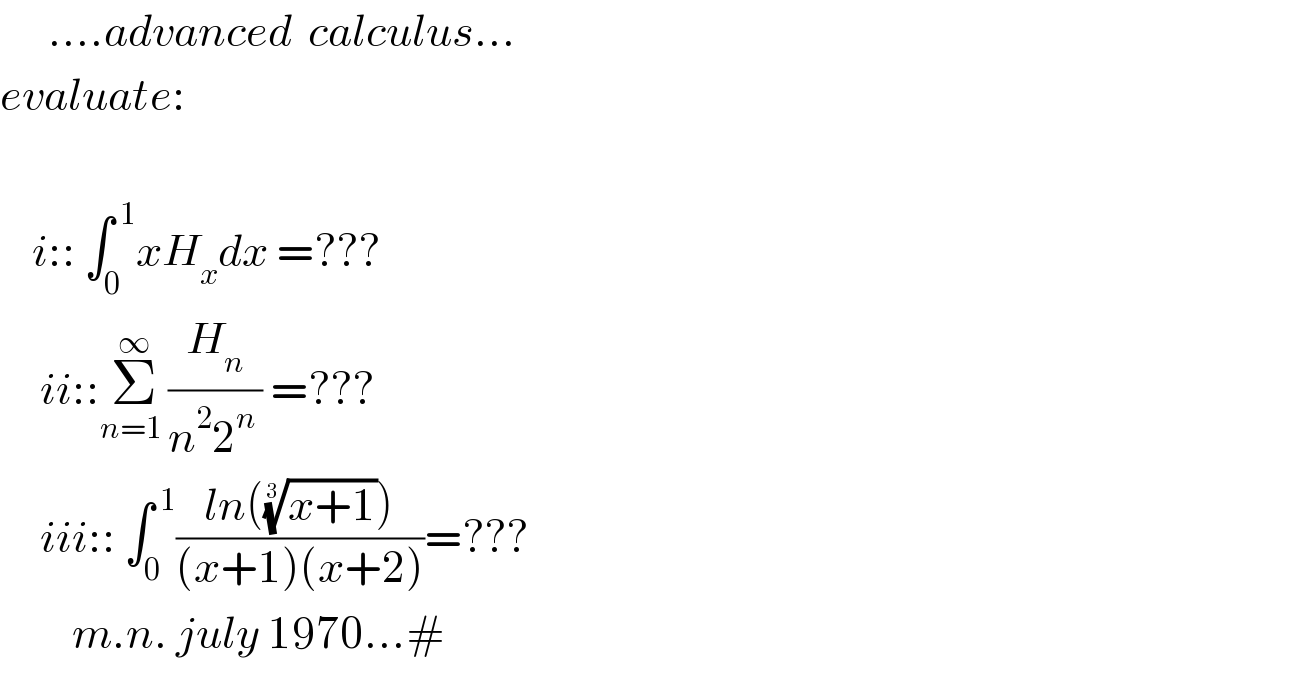
	Answered by mindispower last updated on 05/Sep/20
	$∫_0 ^1 ((ln(x+1))/((x+1)(x+2)))dx ∫_0 ^1 ((ln(x+1))/(x+1))dx_(=A) −∫_0 ^1 ((ln(x+1))/(x+2))dx_(=B) A=(1/2)[ln^2 (x+1)]_0 ^1 =((ln^2 (2))/2) B=−[ln(x+1)ln(x+2)]_0 ^1 +∫_0 ^1 ((ln(x+2))/(x+1))dx By part and x+1=u⇒ B=−ln(2)ln(3)+∫_1 ^2 ((ln(u+1))/u)du u=−y⇒B=−ln(2)ln(3)+∫_(−1) ^(−2) ((ln(1−y))/y)dy B=−ln(2)ln(3)−[−∫_(−1) ^(−2) ((ln(1−y))/y)dy] =−ln(2)ln(3)−Li_2 (−2)+Li_2 (−1) Li_2 (z)=Σ(z^k /k^2 ) Li_2 (−1)=Σ_(k≥1) (1/(4k^2 ))−Σ_(k≥0) (1/((2k+1)^2 ))=((ζ(2))/4)−{ζ(2)−((ζ(2))/4)} =−(1/2)=−(1/2)ζ(2)=−(π^2 /(12)) ∫_0 ^1 ((ln(x+1))/((x+1)(x+2)))dx=A+B=((ln^2 (2))/2)−ln(2)ln(3)−Li_2 (−2)−(π^2 /(12)) =−Li_2 (−2)−(1/2)ln(2)ln((2/9))−(π^2 /(12))$
	$\int_{0}^{1} \frac{l n (x + 1)}{(x + 1) (x + 2)} d x$ $\int_{0}^{1} \frac{l n (x + 1)}{x + 1} {d x}_{= A} - \int_{0}^{1} \frac{l n (x + 1)}{x + 2} d \underset{= B}{x}$ $A = \frac{1}{2} {[{l n}^{2} (x + 1)]}_{0}^{1} = \frac{{l n}^{2} (2)}{2}$ $B = - {[l n (x + 1) l n (x + 2)]}_{0}^{1} + \int_{0}^{1} \frac{l n (x + 2)}{x + 1} d x$ $B y p a r t a n d x + 1 = u \Rightarrow$ $B = - l n (2) l n (3) + \int_{1}^{2} \frac{l n (u + 1)}{u} d u$ $u = - y \Rightarrow B = - l n (2) l n (3) + \int_{- 1}^{- 2} \frac{l n (1 - y)}{y} d y$ $B = - l n (2) l n (3) - [- \int_{- 1}^{- 2} \frac{l n (1 - y)}{y} d y]$ $= - l n (2) l n (3) - {L i}_{2} (- 2) + {L i}_{2} (- 1)$ ${L i}_{2} (z) = Σ \frac{z^{k}}{k^{2}}$ ${L i}_{2} (- 1) = \sum_{k ⩾ 1} \frac{1}{4 k^{2}} - \sum_{k ⩾ 0} \frac{1}{{(2 k + 1)}^{2}} = \frac{ζ (2)}{4} - {ζ (2) - \frac{ζ (2)}{4}}$ $= - \frac{1}{2} = - \frac{1}{2} ζ (2) = - \frac{π^{2}}{12}$ $\int_{0}^{1} \frac{l n (x + 1)}{(x + 1) (x + 2)} d x = A + B = \frac{{l n}^{2} (2)}{2} - l n (2) l n (3) - {L i}_{2} (- 2) - \frac{π^{2}}{12}$ $= - {L i}_{2} (- 2) - \frac{1}{2} l n (2) l n (\frac{2}{9}) - \frac{π^{2}}{12}$
	Commented by mathdave last updated on 06/Sep/20

	$m i s t a k e f r o m t h e f i r s t s t e p$
	Commented by mathdave last updated on 06/Sep/20

	$i t s u p p o s e d t o b e s o m e t h i n g l i k e t h i s$ $\int_{0}^{1} \frac{\ln {(1 + x)}^{\frac{1}{3}}}{(1 + x) (2 + x)} d x = \frac{1}{3} \int_{0}^{1} \frac{\ln (1 + x)}{(1 + x)} d x - \frac{1}{3} \int_{0}^{1} \frac{\ln (1 + x)}{(2 + x)} d x$
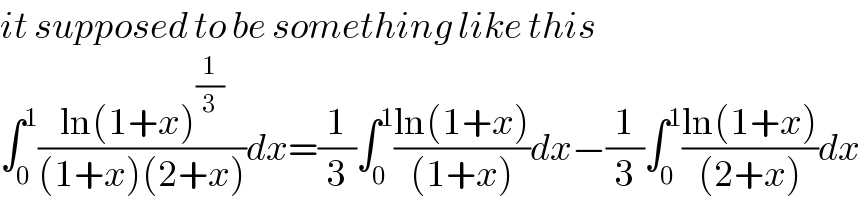
	Commented by mindispower last updated on 06/Sep/20

	$i h a v e s t a r t e w i t h e \int_{0}^{1} \frac{l n (x + 1)}{(1 + x) (2 + x)} d x$ $j u s t b e c a u s e i d o n t w a n t w r i t e e v r e y s t e p s \frac{1}{3}$
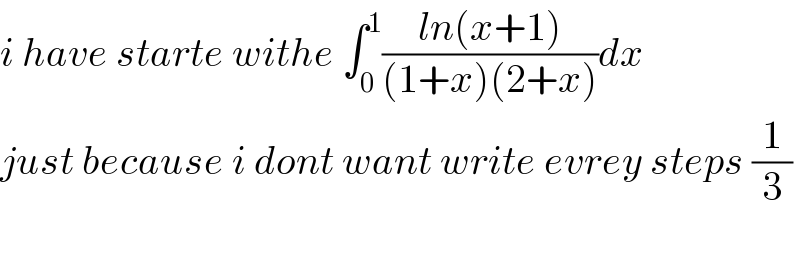
	Commented by mathdave last updated on 06/Sep/20

	$a s i d e t h a t u d o n t w a m n a u s e d$ $e v e r y t h i n g w h e n g e t t i n g u r f i n a l$ $a n s w e r \frac{1}{3} w a s n t r e f l e c t i n g t h e r e$
	Commented by mnjuly1970 last updated on 06/Sep/20

	$t h a n k y o u s o m u c h f o r y o u$ $c a r e f u l n e s s . . .$
	Commented by mnjuly1970 last updated on 06/Sep/20

	$t h a n k y o u s o m u c h f o r y o u r$ $e f f o r t . g r a t e f u l . . . .$
	Commented by Tawa11 last updated on 06/Sep/21

	$grest sir$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum