Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 112011 by Aina Samuel Temidayo last updated on 05/Sep/20

Find ∣{n∈N∣n≤100, 4!∣2^n −n^3 }∣. (Note that ∣S∣ denotes the cardinality or number of elements of a set,S).

$$\mathrm{Find}\:\mid\left\{\mathrm{n}\in\mathbb{N}\mid\mathrm{n}\leqslant\mathrm{100},\:\mathrm{4}!\mid\mathrm{2}^{\mathrm{n}} −\mathrm{n}^{\mathrm{3}} \right\}\mid. \\ $$$$\left(\mathrm{Note}\:\mathrm{that}\:\mid\mathrm{S}\mid\:\mathrm{denotes}\:\mathrm{the}\:\mathrm{cardinality}\right. \\ $$$$\left.\mathrm{or}\:\mathrm{number}\:\mathrm{of}\:\mathrm{elements}\:\mathrm{of}\:\mathrm{a}\:\mathrm{set},\mathrm{S}\right). \\ $$

Answered by Rasheed.Sindhi last updated on 07/Sep/20

n may be odd or even. ^▶ n=2k+1 2^n −n^3 =2^(2k+1) −(2k+1)^3 =2.4^k −(8k^3 +1+3(2k)(2k+1)) =2.4^k −8k^3 −1−12k^2 −6k =2.4^k −8k^3 −12k^2 −6k−1 =an odd number(not divisible by 4) ^▶ n=2k 2^n −n^3 =2^(2k) −(2k)^3 =4^k −8k^3 =4(4^(k−1) −2k^3 ) ^▶ Hence only for n∈E 4 ∣ 2^n −n^3 ^▶ Even numbers upto 100 is 50 This proves that ∣{n∈N∣n≤100, 4!∣2^n −n^3 }∣=50 Recall that I considerd N={1,2,3,...} ( If we consider N={0,1,2,3,...} Then the answer is 51)

$${n}\:{may}\:{be}\:{odd}\:{or}\:{even}. \\ $$$$\:^{\blacktriangleright} {n}=\mathrm{2}{k}+\mathrm{1} \\ $$$$\:\:\:\:\:\mathrm{2}^{\mathrm{n}} −\mathrm{n}^{\mathrm{3}} =\mathrm{2}^{\mathrm{2}{k}+\mathrm{1}} −\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:=\mathrm{2}.\mathrm{4}^{{k}} −\left(\mathrm{8}{k}^{\mathrm{3}} +\mathrm{1}+\mathrm{3}\left(\mathrm{2}{k}\right)\left(\mathrm{2}{k}+\mathrm{1}\right)\right) \\ $$$$\:\:\:\:\:=\mathrm{2}.\mathrm{4}^{{k}} −\mathrm{8}{k}^{\mathrm{3}} −\mathrm{1}−\mathrm{12}{k}^{\mathrm{2}} −\mathrm{6}{k} \\ $$$$\:\:\:\:\:=\mathrm{2}.\mathrm{4}^{{k}} −\mathrm{8}{k}^{\mathrm{3}} −\mathrm{12}{k}^{\mathrm{2}} −\mathrm{6}{k}−\mathrm{1} \\ $$$$\:\:\:\:={an}\:{odd}\:{number}\left({not}\:{divisible}\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{by}\:\:\mathrm{4}\right) \\ $$$$\:^{\blacktriangleright} {n}=\mathrm{2}{k} \\ $$$$\:\:\:\:\:\:\:\mathrm{2}^{\mathrm{n}} −\mathrm{n}^{\mathrm{3}} =\mathrm{2}^{\mathrm{2}{k}} −\left(\mathrm{2}{k}\right)^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}^{{k}} −\mathrm{8}{k}^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}\left(\mathrm{4}^{{k}−\mathrm{1}} −\mathrm{2}{k}^{\mathrm{3}} \right) \\ $$$$\:^{\blacktriangleright} \mathcal{H}{ence}\:{only}\:{for}\:{n}\in\mathbb{E} \\ $$$$\:\:\:\:\:\:\mathrm{4}\:\mid\:\mathrm{2}^{\mathrm{n}} −\mathrm{n}^{\mathrm{3}} \\ $$$$\:^{\blacktriangleright} \mathcal{E}{ven}\:{numbers}\:{upto}\:\mathrm{100}\:{is}\:\mathrm{50} \\ $$$${This}\:{proves}\:{that} \\ $$$$\mid\left\{\mathrm{n}\in\mathbb{N}\mid\mathrm{n}\leqslant\mathrm{100},\:\mathrm{4}!\mid\mathrm{2}^{\mathrm{n}} −\mathrm{n}^{\mathrm{3}} \right\}\mid=\mathrm{50} \\ $$$${Recall}\:{that}\:{I}\:{considerd}\: \\ $$$$\:\:\:\mathbb{N}=\left\{\mathrm{1},\mathrm{2},\mathrm{3},...\right\} \\ $$$$\:\left(\:{If}\:{we}\:{consider}\right. \\ $$$$\:\:\:\mathbb{N}=\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},...\right\} \\ $$$$\left.\:\:\:\:{Then}\:{the}\:{answer}\:{is}\:\mathrm{51}\right) \\ $$

Commented by Rasheed.Sindhi last updated on 07/Sep/20

Sorry I can′t do it.However with the help of calculator, the numbers are 4,10,16,....,6n−2 So the number of these numbers upto 100 is 17

$${Sorry}\:{I}\:{can}'{t}\:{do}\:{it}.{However} \\ $$$${with}\:{the}\:{help}\:{of}\:{calculator},\:{the} \\ $$$${numbers}\:{are}\:\mathrm{4},\mathrm{10},\mathrm{16},....,\mathrm{6}{n}−\mathrm{2} \\ $$$${So}\:{the}\:{number}\:{of}\:{these}\:{numbers} \\ $$$${upto}\:\mathrm{100}\:{is}\:\mathrm{17} \\ $$

Commented by kaivan.ahmadi last updated on 05/Sep/20

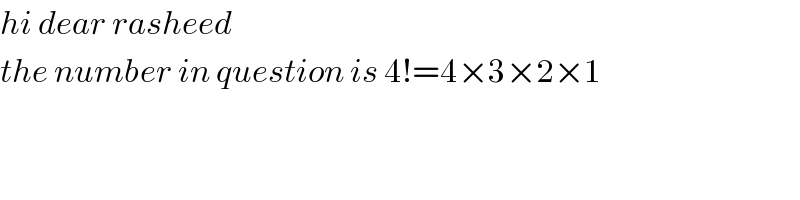
hi dear rasheed the number in question is 4!=4×3×2×1

$${hi}\:{dear}\:{rasheed} \\ $$$${the}\:{number}\:{in}\:{question}\:{is}\:\mathrm{4}!=\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{1} \\ $$

Commented by Rasheed.Sindhi last updated on 05/Sep/20

Misreading sir misreading! I′ll review my answer. ThanX dear kaivan!

$${Misreading}\:{sir}\:{misreading}! \\ $$$${I}'{ll}\:{review}\:{my}\:{answer}. \\ $$$$\mathcal{T}{han}\mathcal{X}\:\:{dear}\:{kaivan}! \\ $$

Commented by Aina Samuel Temidayo last updated on 06/Sep/20

Please I′m still waiting for the correction. Thanks.

$$\mathrm{Please}\:\mathrm{I}'\mathrm{m}\:\mathrm{still}\:\mathrm{waiting}\:\mathrm{for}\:\mathrm{the} \\ $$$$\mathrm{correction}.\:\mathrm{Thanks}. \\ $$

Answered by Rasheed.Sindhi last updated on 09/Sep/20

4! ∣ 2^n −n^3 24∣2^n −n^3 2^n ≡n^3 (mod 24) Let { ((2^n ≡u(mod 24))),((n^3 ≡v(mod 24)) :} [(n,(2^n mod 24_((u)) ),(n^3 mod 24_((v)) ),),(1,( 2),( 1),),(2,( 4),( 8),),(3,( 8),( 3),),(4,( 16),( 16),(u=v)),(5,( 8),( 5),),(6,( 16),( 0),),(7,( 8),( 7),),(8,( 16),( 8),),(9,( 8),( 9),),((10),( 16),( 16),(u=v)),((11),( 8),( 11),),((12),( 16),( 0),),((13),( 8),( 13),),((14),( 16),( 8),),((15),( 8),( 15),),((16),( 16),( 16),(u=v)),((17),( 8),( 17),),((18),( 16),( 0),),((19),( 8),( 19),),((20),( 16),( 8),),((21),( 8),( 21),),((22),( 16),( 16),(u=v)),((23),( 8),( 23),),((24),( 16),( 0),) ] Values of n for which u=v or 2^n ≡n^3 (mod 24) or in other words 4! ∣ 2^n −n^3 are: 4,10,16,...(6n−2).. This is an AP upto 100 of which are 17 terms. ∴ 4! ∣ 2^n −n^3 has 17 solutions for n∈N ∧ n≤100.

$$\mathrm{4}!\:\mid\:\mathrm{2}^{\mathrm{n}} −\mathrm{n}^{\mathrm{3}} \\ $$$$\mathrm{24}\mid\mathrm{2}^{\mathrm{n}} −\mathrm{n}^{\mathrm{3}} \\ $$$$\mathrm{2}^{{n}} \equiv{n}^{\mathrm{3}} \left({mod}\:\mathrm{24}\right) \\ $$$$ \\ $$$${Let}\:\begin{cases}{\mathrm{2}^{{n}} \equiv{u}\left({mod}\:\mathrm{24}\right)}\\{{n}^{\mathrm{3}} \equiv{v}\left({mod}\:\mathrm{24}\right.}\end{cases} \\ $$$$\:\:\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\begin{bmatrix}{{n}}&{\underset{\left({u}\right)} {\mathrm{2}^{{n}} {mod}\:\mathrm{24}}}&{\underset{\left({v}\right)} {{n}^{\mathrm{3}} {mod}\:\mathrm{24}}}&{}\\{\mathrm{1}}&{\:\:\:\:\:\:\:\:\:\mathrm{2}}&{\:\:\:\:\:\:\:\mathrm{1}}&{}\\{\mathrm{2}}&{\:\:\:\:\:\:\:\:\mathrm{4}}&{\:\:\:\:\:\:\:\mathrm{8}}&{}\\{\mathrm{3}}&{\:\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\:\:\:\:\:\mathrm{3}}&{}\\{\mathrm{4}}&{\:\:\:\:\:\:\mathrm{16}}&{\:\:\:\:\:\mathrm{16}}&{{u}={v}}\\{\mathrm{5}}&{\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\:\:\:\:\mathrm{5}}&{}\\{\mathrm{6}}&{\:\:\:\:\:\mathrm{16}}&{\:\:\:\:\:\:\mathrm{0}}&{}\\{\mathrm{7}}&{\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\:\:\:\mathrm{7}}&{}\\{\mathrm{8}}&{\:\:\:\:\:\mathrm{16}}&{\:\:\:\:\:\mathrm{8}}&{}\\{\mathrm{9}}&{\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\:\:\:\mathrm{9}}&{}\\{\mathrm{10}}&{\:\:\:\:\:\mathrm{16}}&{\:\:\:\mathrm{16}}&{{u}={v}}\\{\mathrm{11}}&{\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\:\mathrm{11}}&{}\\{\mathrm{12}}&{\:\:\:\:\:\mathrm{16}}&{\:\:\:\:\mathrm{0}}&{}\\{\mathrm{13}}&{\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\:\mathrm{13}}&{}\\{\mathrm{14}}&{\:\:\:\:\:\mathrm{16}}&{\:\:\:\:\mathrm{8}}&{}\\{\mathrm{15}}&{\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\mathrm{15}}&{}\\{\mathrm{16}}&{\:\:\:\:\:\mathrm{16}}&{\:\:\mathrm{16}}&{{u}={v}}\\{\mathrm{17}}&{\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\mathrm{17}}&{}\\{\mathrm{18}}&{\:\:\:\:\:\mathrm{16}}&{\:\:\:\mathrm{0}}&{}\\{\mathrm{19}}&{\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\mathrm{19}}&{}\\{\mathrm{20}}&{\:\:\:\:\:\mathrm{16}}&{\:\:\:\mathrm{8}}&{}\\{\mathrm{21}}&{\:\:\:\:\:\:\mathrm{8}}&{\:\:\mathrm{21}}&{}\\{\mathrm{22}}&{\:\:\:\:\mathrm{16}}&{\:\:\mathrm{16}}&{{u}={v}}\\{\mathrm{23}}&{\:\:\:\:\:\:\:\mathrm{8}}&{\:\:\mathrm{23}}&{}\\{\mathrm{24}}&{\:\:\:\:\mathrm{16}}&{\:\:\:\mathrm{0}}&{}\end{bmatrix} \\ $$$${Values}\:{of}\:{n}\:{for}\:{which}\:{u}={v}\:{or} \\ $$$$\mathrm{2}^{{n}} \equiv{n}^{\mathrm{3}} \left({mod}\:\mathrm{24}\right)\:{or}\:{in}\:{other}\:{words} \\ $$$$\mathrm{4}!\:\mid\:\mathrm{2}^{{n}} −{n}^{\mathrm{3}} \:{are}: \\ $$$$\:\mathrm{4},\mathrm{10},\mathrm{16},...\left(\mathrm{6}{n}−\mathrm{2}\right).. \\ $$$$\mathcal{T}{his}\:{is}\:{an}\:{AP}\:{upto}\:\mathrm{100}\:{of}\:{which} \\ $$$${are}\:\mathrm{17}\:{terms}. \\ $$$$\therefore\:\mathrm{4}!\:\mid\:\mathrm{2}^{\boldsymbol{{n}}} −\boldsymbol{{n}}^{\mathrm{3}} \:\boldsymbol{{has}}\:\mathrm{17}\:\boldsymbol{{solutions}} \\ $$$$\:\:\:\:\:\boldsymbol{{for}}\:\boldsymbol{{n}}\in\mathbb{N}\:\wedge\:\boldsymbol{{n}}\leqslant\mathrm{100}. \\ $$

Commented by Aina Samuel Temidayo last updated on 07/Sep/20

Can you please complete it?

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{please}\:\mathrm{complete}\:\mathrm{it}? \\ $$

Commented by Rasheed.Sindhi last updated on 09/Sep/20

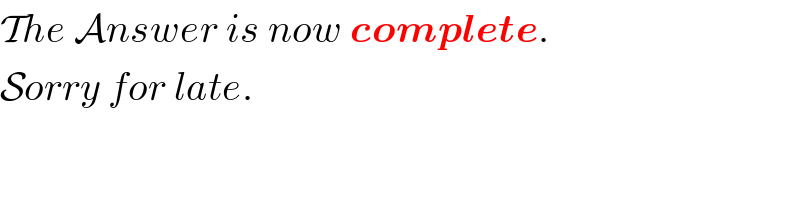
The Answer is now complete. Sorry for late.

$$\mathcal{T}{he}\:\mathcal{A}{nswer}\:{is}\:{now}\:\boldsymbol{{complete}}. \\ $$$$\mathcal{S}{orry}\:{for}\:{late}. \\ $$

Commented by Aina Samuel Temidayo last updated on 09/Sep/20

Thanks.

$$\mathrm{Thanks}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com