
Question and Answers Forum
Question Number 112119 by mnjuly1970 last updated on 06/Sep/20
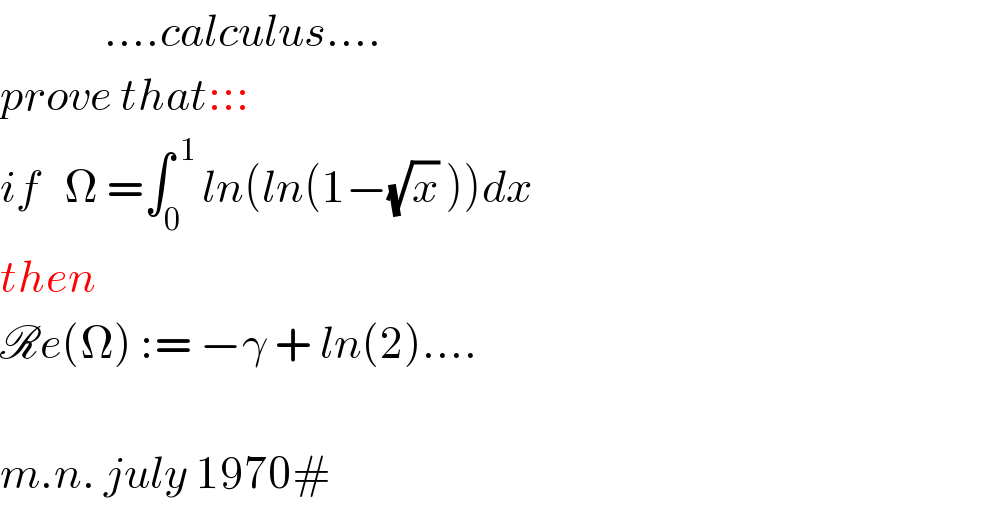
Answered by maths mind last updated on 06/Sep/20
![u=ln(1−(√x))⇒x=(1−e^u )^2 ⇒dx=−2e^u (1−e^u )du Ω=∫_0 ^(−∞) ln(u).−2e^u (1−e^u )du we use ln(z)=ln∣z∣+iarg(z) z∉IR_− ^∗ put u=−t⇒=∫_0 ^∞ ln(−t).2e^(−t) (1−e^(−t) )dt =∫_0 ^∞ (ln(t)+iπ)2e^t (1−e^t )dt Re(Ω)=∫_0 ^∞ 2ln(t)e^(−t) dt−2∫_0 ^∞ ln(t)e^(−2t) dt Γ(z)=∫_0 ^∞ t^(z−1) e^(−t) dt⇒Γ′(1)=∫_0 ^(+∞) ln(t)e^(−t) dt=γ Re(Ω)=−2γ−2∫_0 ^(+∞) ln((s/2))e^(−s) .(ds/2) =−2γ−∫_0 ^(+∞) ln(s)e^(−s) ds+ln(2)∫_0 ^(+∞) e^(−s) ds =−2γ+γ+ln(2)[−e^(−s) ]_0 ^(+∞) =−γ+ln(2)](Q112178.png)
Commented by mnjuly1970 last updated on 06/Sep/20

| ||
Question and Answers Forum | ||
Question Number 112119 by mnjuly1970 last updated on 06/Sep/20 | ||
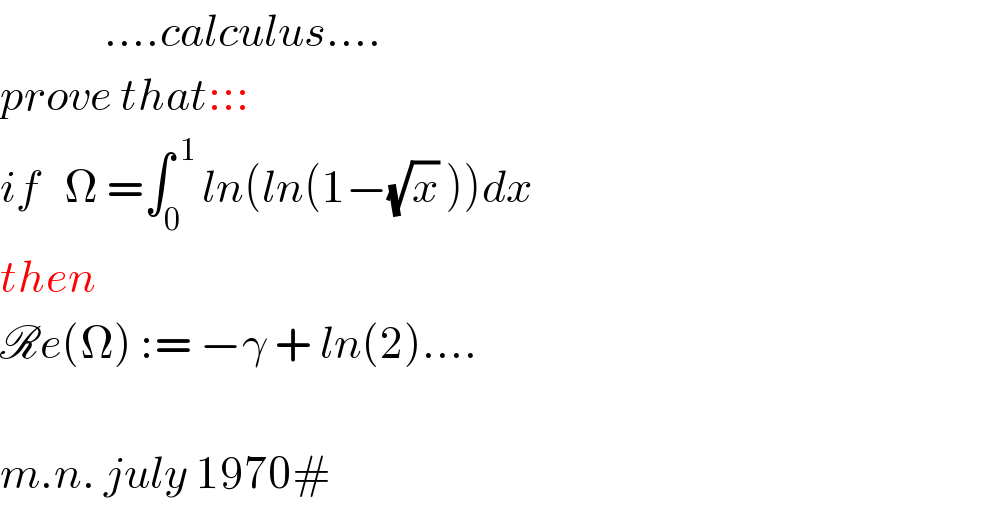 | ||
Answered by maths mind last updated on 06/Sep/20 | ||
![u=ln(1−(√x))⇒x=(1−e^u )^2 ⇒dx=−2e^u (1−e^u )du Ω=∫_0 ^(−∞) ln(u).−2e^u (1−e^u )du we use ln(z)=ln∣z∣+iarg(z) z∉IR_− ^∗ put u=−t⇒=∫_0 ^∞ ln(−t).2e^(−t) (1−e^(−t) )dt =∫_0 ^∞ (ln(t)+iπ)2e^t (1−e^t )dt Re(Ω)=∫_0 ^∞ 2ln(t)e^(−t) dt−2∫_0 ^∞ ln(t)e^(−2t) dt Γ(z)=∫_0 ^∞ t^(z−1) e^(−t) dt⇒Γ′(1)=∫_0 ^(+∞) ln(t)e^(−t) dt=γ Re(Ω)=−2γ−2∫_0 ^(+∞) ln((s/2))e^(−s) .(ds/2) =−2γ−∫_0 ^(+∞) ln(s)e^(−s) ds+ln(2)∫_0 ^(+∞) e^(−s) ds =−2γ+γ+ln(2)[−e^(−s) ]_0 ^(+∞) =−γ+ln(2)](Q112178.png) | ||
| ||
Commented by mnjuly1970 last updated on 06/Sep/20 | ||
 | ||