Question Number 112271 by bemath last updated on 07/Sep/20
$$\:\:\:\:\sqrt{\mathrm{bemath}} \\ $$$$\:\:\:\int\:\mathrm{sin}\:\mathrm{x}\:\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}\:\mathrm{dx}\:? \\ $$
Answered by maths mind last updated on 07/Sep/20
$$\mathrm{1}−{sin}\left({x}\right)=\left({sin}\left(\frac{{x}}{\mathrm{2}}\right)−{cos}\left(\frac{{x}}{\mathrm{2}}\right)\right)^{\mathrm{2}} \\ $$
Commented by bemath last updated on 07/Sep/20
$$\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{x}}\:=\:\mid\mathrm{sin}\:\frac{\mathrm{x}}{\mathrm{2}}−\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}\mid\: \\ $$
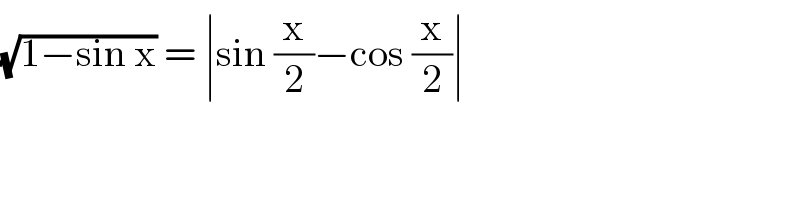
Answered by MJS_new last updated on 07/Sep/20
![∫sin x (√(1−sin x)) dx= [t=sin x → dx=(dt/(cos x))] =∫((t(√(1−t)))/( (√(1−t^2 ))))dt=∫(t/( (√(1+t))))dt=(2/3)(t−2)(√(t+1)) but we′re losing sign changes... other idea ∫sin x (√(1−sin x)) dx= [t=(x/2)−(π/4) → dx=2dt] =2∫cos 2t (√(1−cos 2t)) dt= =2∫(2cos^2 t −1)(√(1−(2cos^2 t −1)))dt= =2(√2)∫(2cos^2 t −1)(√(1−cos^2 t)) dt= =2(√2)∫(2cos^2 t sin t −sin t)dt= =(√2)∫(sin 3t −sin t)dt= =(√2)cos t −((√2)/3)cos 3t =... but we′re also losing sign changes](Q112352.png)
$$\int\mathrm{sin}\:{x}\:\sqrt{\mathrm{1}−\mathrm{sin}\:{x}}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sin}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{cos}\:{x}}\right] \\ $$$$=\int\frac{{t}\sqrt{\mathrm{1}−{t}}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt}=\int\frac{{t}}{\:\sqrt{\mathrm{1}+{t}}}{dt}=\frac{\mathrm{2}}{\mathrm{3}}\left({t}−\mathrm{2}\right)\sqrt{{t}+\mathrm{1}} \\ $$$$\mathrm{but}\:\mathrm{we}'\mathrm{re}\:\mathrm{losing}\:\mathrm{sign}\:\mathrm{changes}... \\ $$$$\mathrm{other}\:\mathrm{idea} \\ $$$$\int\mathrm{sin}\:{x}\:\sqrt{\mathrm{1}−\mathrm{sin}\:{x}}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\:\rightarrow\:{dx}=\mathrm{2}{dt}\right] \\ $$$$=\mathrm{2}\int\mathrm{cos}\:\mathrm{2}{t}\:\sqrt{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{t}}\:{dt}= \\ $$$$=\mathrm{2}\int\left(\mathrm{2cos}^{\mathrm{2}} \:{t}\:−\mathrm{1}\right)\sqrt{\mathrm{1}−\left(\mathrm{2cos}^{\mathrm{2}} \:{t}\:−\mathrm{1}\right)}{dt}= \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\int\left(\mathrm{2cos}^{\mathrm{2}} \:{t}\:−\mathrm{1}\right)\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:{t}}\:{dt}= \\ $$$$=\mathrm{2}\sqrt{\mathrm{2}}\int\left(\mathrm{2cos}^{\mathrm{2}} \:{t}\:\mathrm{sin}\:{t}\:−\mathrm{sin}\:{t}\right){dt}= \\ $$$$=\sqrt{\mathrm{2}}\int\left(\mathrm{sin}\:\mathrm{3}{t}\:−\mathrm{sin}\:{t}\right){dt}= \\ $$$$=\sqrt{\mathrm{2}}\mathrm{cos}\:{t}\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\mathrm{cos}\:\mathrm{3}{t}\:=... \\ $$$$\mathrm{but}\:\mathrm{we}'\mathrm{re}\:\mathrm{also}\:\mathrm{losing}\:\mathrm{sign}\:\mathrm{changes} \\ $$
Commented by MJS_new last updated on 07/Sep/20
![found it! we must somehow keep the factor (√(1−sin x)) in the result. ∫sin x (√(1−sin x)) dx= [t=sin x → dx=(dt/(cos x))] =∫((t(√(1−t)))/( (√(1−t^2 ))))dt= [u=((√(1−t))/( (√(1−t^2 )))) → dt=−((2(t+1)(√(1−t^2 )))/( (√(1−t))))] =2∫((1/u^2 )−(1/u^4 ))du=(2/(3u^3 ))−(2/u)= =((2(t−2)(√(1−t^2 )))/(3(√(1−t))))= =((2(sin x −2)cos x)/(3(√(1−sin x))))+C](Q112354.png)
$$\mathrm{found}\:\mathrm{it}!\:\mathrm{we}\:\mathrm{must}\:\mathrm{somehow}\:\mathrm{keep}\:\mathrm{the}\:\mathrm{factor} \\ $$$$\sqrt{\mathrm{1}−\mathrm{sin}\:{x}}\:\mathrm{in}\:\mathrm{the}\:\mathrm{result}. \\ $$$$ \\ $$$$\int\mathrm{sin}\:{x}\:\sqrt{\mathrm{1}−\mathrm{sin}\:{x}}\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sin}\:{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{cos}\:{x}}\right] \\ $$$$=\int\frac{{t}\sqrt{\mathrm{1}−{t}}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\sqrt{\mathrm{1}−{t}}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\:\rightarrow\:{dt}=−\frac{\mathrm{2}\left({t}+\mathrm{1}\right)\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{t}}}\right] \\ $$$$=\mathrm{2}\int\left(\frac{\mathrm{1}}{{u}^{\mathrm{2}} }−\frac{\mathrm{1}}{{u}^{\mathrm{4}} }\right){du}=\frac{\mathrm{2}}{\mathrm{3}{u}^{\mathrm{3}} }−\frac{\mathrm{2}}{{u}}= \\ $$$$=\frac{\mathrm{2}\left({t}−\mathrm{2}\right)\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{\mathrm{3}\sqrt{\mathrm{1}−{t}}}= \\ $$$$=\frac{\mathrm{2}\left(\mathrm{sin}\:{x}\:−\mathrm{2}\right)\mathrm{cos}\:{x}}{\mathrm{3}\sqrt{\mathrm{1}−\mathrm{sin}\:{x}}}+{C} \\ $$