Question and Answers Forum
Question Number 112403 by ajfour last updated on 07/Sep/20
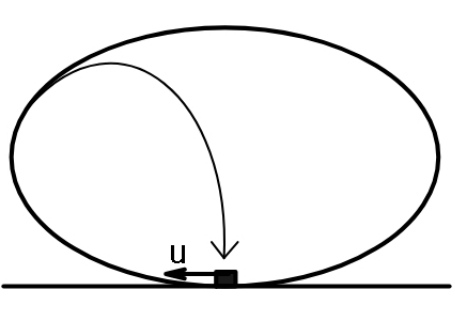
Commented by ajfour last updated on 07/Sep/20

Answered by mr W last updated on 07/Sep/20
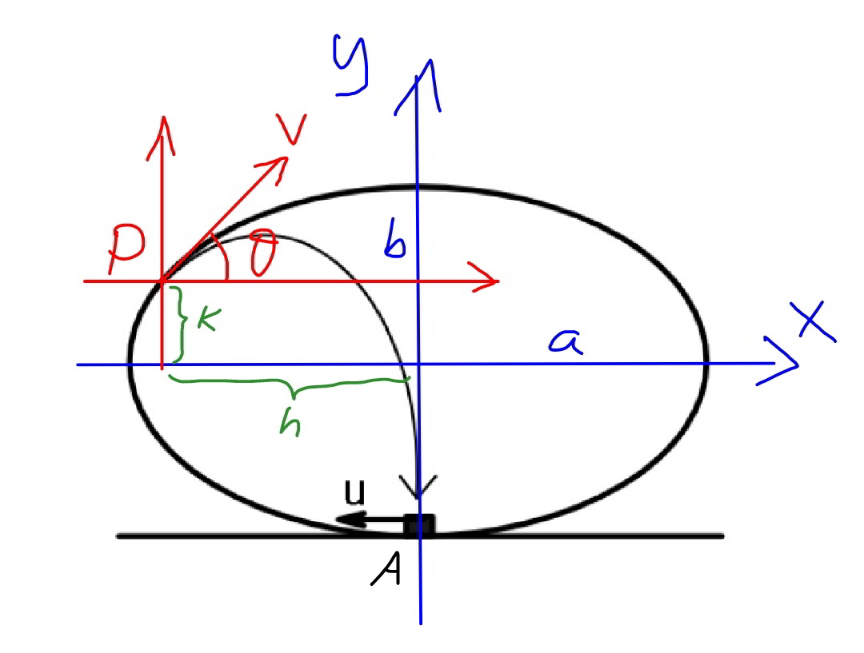
Commented by mr W last updated on 08/Sep/20
![P(−h, k) h=a cos ϕ k=b sin ϕ tan θ=(b/(a tan ϕ))=(μ/(tan ϕ)) ((mu^2 )/2)=((mv^2 )/2)+mg(b+k) ⇒u^2 =v^2 +2μga(1+sin ϕ) t=(h/(v cos θ)) k+b=−v sin θ×(h/(v cos θ))+(1/2)g((h/(v cos θ)))^2 k+b=−h tan θ+((gh^2 (1+tan^2 θ))/(2v^2 )) ⇒(v^2 /(ga))=((sin ϕ (1−sin ϕ))/(2μ))(1−μ^2 +(μ^2 /(sin^2 ϕ))) y′=(μ/(tan ϕ)) y′′=((dy′)/dx)=((dy′)/dϕ)×(1/(dx/dϕ))=−(μ/(a sin^3 ϕ)) R=∣(((1+y′^2 )^(3/2) )/(y′′))∣ R=((a sin^3 ϕ(1+(μ^2 /(tan^2 ϕ)))^(3/2) )/μ) mg cos θ=((mv^2 )/R) (√(1/(1+(μ^2 /(tan^2 ϕ)))))=((μ[((sin ϕ (1−sin ϕ))/(2μ))(1−μ^2 +(μ^2 /(sin^2 ϕ)))])/(sin^3 ϕ(1+(μ^2 /(tan^2 ϕ)))^(3/2) )) ⇒2(1+sin ϕ)(μ^2 +tan^2 ϕ)=1−μ^2 +(μ^2 /(sin^2 ϕ)) ⇒2sin^2 ϕ[μ^2 +(1−μ^2 )sin^2 ϕ]=(1−sin ϕ)[μ^2 +(1−μ^2 )sin^2 ϕ] ⇒(2sin^2 ϕ+sin ϕ−1)[μ^2 +(1−μ^2 )sin^2 ϕ]=0 ⇒2sin^2 ϕ+sin ϕ−1=0 ⇒(2 sin ϕ−1)(sin ϕ+1)=0 ⇒sin ϕ=(1/2)⇒ϕ=(π/6)for any μ. ⇒(v^2 /(ga))=(( 1+3μ^2 )/(8μ)) ⇒(u^2 /(ga))=((1+27μ^2 )/(8μ))](Q112433.png)
Commented by mr W last updated on 08/Sep/20
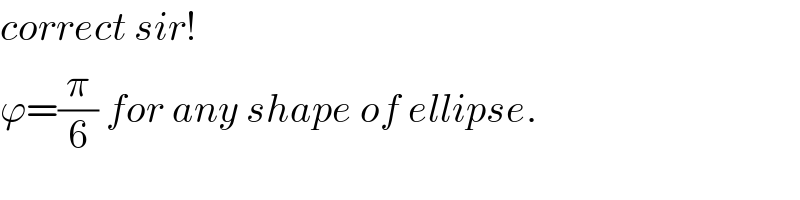
Commented by mr W last updated on 08/Sep/20

Commented by mr W last updated on 08/Sep/20
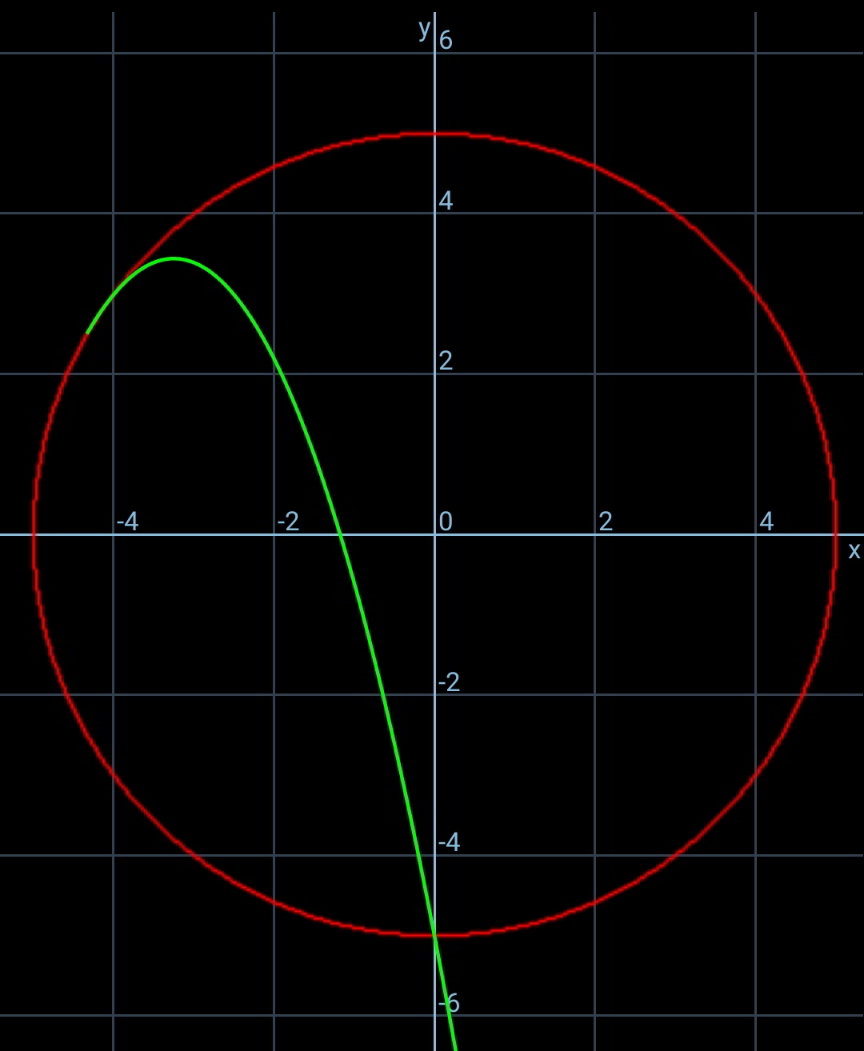
Commented by ajfour last updated on 08/Sep/20
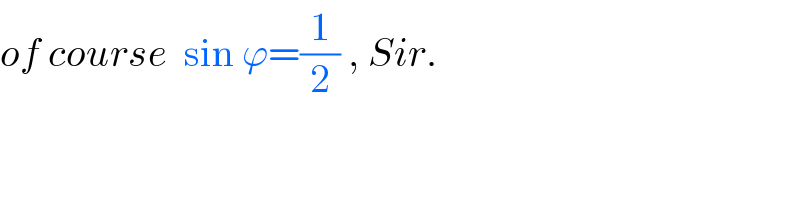
Commented by ajfour last updated on 08/Sep/20
![If μ^2 +(1−μ^2 )sin^2 ϕ=0 μ > 1 , Sir. And sir please explain me R= (( [1+((dy/dx))^2 ]^(3/2) )/(−((d^2 y/dx^2 ))))](Q112598.png)
Commented by mr W last updated on 08/Sep/20

Commented by mr W last updated on 08/Sep/20