Question and Answers Forum

All Questions      Topic List

UNKNOWN Questions

Previous in All Question      Next in All Question      

Previous in UNKNOWN      Next in UNKNOWN      

Question Number 11246 by 786786AM last updated on 18/Mar/17

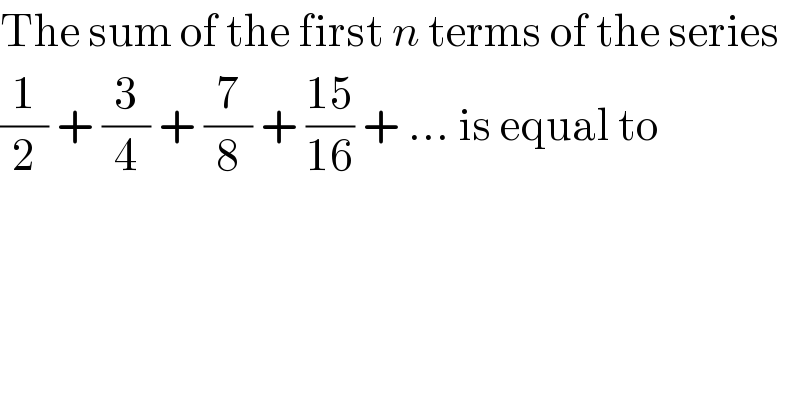
The sum of the first n terms of the series (1/2) + (3/4) + (7/8) + ((15)/(16)) + ... is equal to

$$\mathrm{The}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{first}\:{n}\:\mathrm{terms}\:\mathrm{of}\:\mathrm{the}\:\mathrm{series} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{7}}{\mathrm{8}}\:+\:\frac{\mathrm{15}}{\mathrm{16}}\:+\:...\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$

Answered by FilupS last updated on 18/Mar/17

(1/2) + (3/4) + (7/8) + ((15)/(16)) + ... = Σ_(k=1) ^n ((2^k −1)/2^k ) Σ_(k=1) ^n ((2^k −1)/2^k )=Σ_(k=1) ^n 1−(1/2^k ) =Σ_(k=1) ^n 1−Σ_(k=1) ^n (1/2^k ) =(Σ_(k=1) ^n 1)−S S=Σ_(k=1) ^n (1/2^k ) Σ_(k=1) ^n ((2^k −1)/2^k )=n−S (1) S=Σ_(k=1) ^n (1/2^k ) S=(1/2^1 )+(1/2^2 )+(1/2^3 )+...+(1/2^n ) S=(1/2^1 )(1+(1/2^1 )+(1/2^2 )+...+(1/2^(n−1) )) S=(1/2)(1+S−(1/2^n )) S=(1/2)+(1/2)S−(1/2^(n+1) ) S−(1/2)S=(1/2)−(1/2^(n+1) ) S(1−(1/2))=((2^(n+1) −2)/2^(n+2) ) S(1−(1/2))=((2(2^n −1))/2^(n+2) ) S(1−(1/2))=(((2^n −1))/2^(n+1) ) S=(((2^n −1))/(2^(n+1) (1−(1/2)))) S=(((2^n −1))/(2^(n+1) −(1/2)2^(n+1) )) S=(((2^n −1))/(2^(n+1) −2^n )) S=(((2^n −1))/(2^n (2^1 −1))) S=((2^n −1)/2^n ) (2) sub (2)→(1) Σ_(k=1) ^n ((2^k −1)/2^k )=n−S =n−((2^n −1)/2^n ) =n−((2^n /2^n )−(1/2^n )) =n−(1−(1/2^n )) =n+(1/2^n )−1 ∴Σ_(k=1) ^n ((2^k −1)/2^k ) = (1/2) + (3/4) + ... = n+(1/2^n )−1

$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:\frac{\mathrm{7}}{\mathrm{8}}\:+\:\frac{\mathrm{15}}{\mathrm{16}}\:+\:...\:=\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{2}^{{k}} −\mathrm{1}}{\mathrm{2}^{{k}} } \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{2}^{{k}} −\mathrm{1}}{\mathrm{2}^{{k}} }=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{k}} } \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1}−\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} } \\ $$$$=\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{1}\right)−{S}\:\:\:\:\:\:\:\:\:\:\:{S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} } \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{2}^{{k}} −\mathrm{1}}{\mathrm{2}^{{k}} }={n}−{S}\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\: \\ $$$${S}=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\mathrm{2}^{{k}} } \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+...+\frac{\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right) \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{S}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right) \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{S}−\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$${S}−\frac{\mathrm{1}}{\mathrm{2}}{S}=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$${S}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{2}}{\mathrm{2}^{{n}+\mathrm{2}} } \\ $$$${S}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{2}\left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}^{{n}+\mathrm{2}} } \\ $$$${S}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$${S}=\frac{\left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}^{{n}+\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$${S}=\frac{\left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}^{{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\mathrm{2}^{{n}+\mathrm{1}} } \\ $$$${S}=\frac{\left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{2}^{{n}} } \\ $$$${S}=\frac{\left(\mathrm{2}^{{n}} −\mathrm{1}\right)}{\mathrm{2}^{{n}} \left(\mathrm{2}^{\mathrm{1}} −\mathrm{1}\right)} \\ $$$${S}=\frac{\mathrm{2}^{{n}} −\mathrm{1}}{\mathrm{2}^{{n}} }\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\: \\ $$$$\mathrm{sub}\:\left(\mathrm{2}\right)\rightarrow\left(\mathrm{1}\right) \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{2}^{{k}} −\mathrm{1}}{\mathrm{2}^{{k}} }={n}−{S} \\ $$$$={n}−\frac{\mathrm{2}^{{n}} −\mathrm{1}}{\mathrm{2}^{{n}} } \\ $$$$={n}−\left(\frac{\mathrm{2}^{{n}} }{\mathrm{2}^{{n}} }−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right) \\ $$$$={n}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right) \\ $$$$={n}+\frac{\mathrm{1}}{\mathrm{2}^{{n}} }−\mathrm{1} \\ $$$$\: \\ $$$$\therefore\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{2}^{{k}} −\mathrm{1}}{\mathrm{2}^{{k}} }\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{4}}\:+\:...\:=\:{n}+\frac{\mathrm{1}}{\mathrm{2}^{{n}} }−\mathrm{1} \\ $$

Answered by sandy_suhendra last updated on 18/Mar/17

=(1−(1/2))+(1−(1/4))+(1−(1/8))+... =(1+1+1+...)−((1/2)+(1/4)+(1/8)+...) = n − (((1/2)[1−((1/2))^n ])/(1−(1/2))) = n − 1 + ((1/2))^n

$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\right)+... \\ $$$$=\left(\mathrm{1}+\mathrm{1}+\mathrm{1}+...\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{8}}+...\right) \\ $$$$=\:\mathrm{n}\:−\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}} \right]}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\:\mathrm{n}\:−\:\mathrm{1}\:+\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}} \\ $$

Commented by FilupS last updated on 18/Mar/17

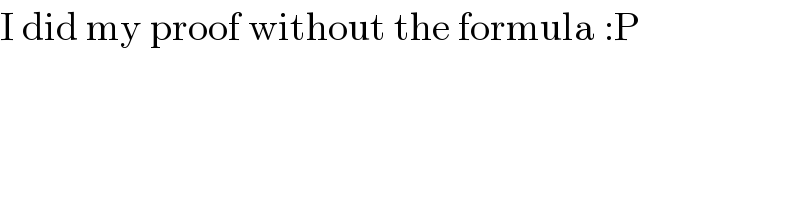
I did my proof without the formula :P

$$\mathrm{I}\:\mathrm{did}\:\mathrm{my}\:\mathrm{proof}\:\mathrm{without}\:\mathrm{the}\:\mathrm{formula}\::\mathrm{P} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com