Question Number 112583 by mohammad17 last updated on 08/Sep/20
Commented by Aziztisffola last updated on 08/Sep/20
$$\mathrm{1}.\:\mathrm{let}\:\sqrt{\mathrm{7}}=\frac{\mathrm{a}}{\mathrm{b}}\:\mathrm{with}\:\mathrm{gcd}\left(\mathrm{a};\mathrm{b}\right)=\mathrm{1}\:\:\left(\mathrm{a}\:\&\mathrm{b}\in\mathbb{Z}\:\mathrm{b}\neq\mathrm{0}\right) \\ $$$$\:\Rightarrow\mathrm{7}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{b}^{\mathrm{2}} }\Rightarrow\mathrm{a}^{\mathrm{2}} =\mathrm{7b}^{\mathrm{2}} \Rightarrow\mathrm{7}\mid\mathrm{a}^{\mathrm{2}} \:\:\:\:\overset{\mathrm{7}\:\mathrm{is}\:\mathrm{prime}\:} {\Rightarrow}\mathrm{7}\mid\mathrm{a} \\ $$$$\Rightarrow\:\mathrm{a}=\mathrm{7k}\:\left(\mathrm{k}\:\in\mathbb{Z}\right) \\ $$$$\Rightarrow\left(\mathrm{7k}\right)^{\mathrm{2}} =\mathrm{7b}^{\mathrm{2}} \Rightarrow\mathrm{b}^{\mathrm{2}} =\mathrm{7k}^{\mathrm{2}} \Rightarrow\mathrm{7}\mid\mathrm{b}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{7}\mid\mathrm{b} \\ $$$$\mathrm{then}\:\mathrm{7}\mid\mathrm{a}\:\&\mathrm{7}\mid\mathrm{b}\:\Rightarrow\mathrm{gcd}\left(\mathrm{a};\mathrm{b}\right)\neq\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{contradiction} \\ $$$$\:\mathrm{hence}\:\sqrt{\mathrm{7}\:}\:\mathrm{is}\:\mathrm{irrational}.\:\sqrt{\mathrm{7}}\notin\mathbb{Q} \\ $$
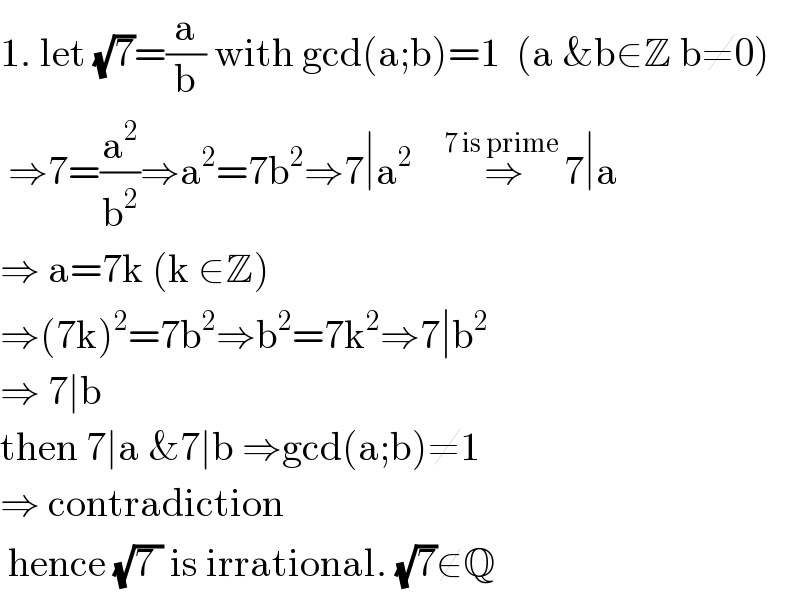
Commented by mohammad17 last updated on 08/Sep/20
$${thank}\:{you}\:{sir}\:{can}\:{you}\:{help}\:{me}\:{in}\:{other}\:{question} \\ $$
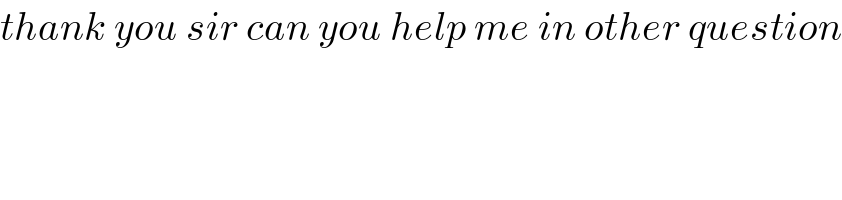
Commented by Aziztisffola last updated on 08/Sep/20
![2. ]0;1[⊂R Suppose we can list all number in ]0;1[ x_1 =0.x_(11) x_(12) x_(13) ... x_2 =0.x_(21) x_(22) x_(23) ... x_3 =0.x_(31) x_(32) x_(33) ... ..... x_(ij) =0,...9 Consider a=0.x_(11) x_(22) x_(33) .... construct the number x=0.a_1 a_2 a_3 ... with a_i ≠x_(ii) (and a_i ≠9) then x≠x_1 ; x≠x_2 .... then x is not in the list hence R is uncountable.](Q112596.png)
$$\left.\mathrm{2}.\:\right]\mathrm{0};\mathrm{1}\left[\subset\mathbb{R}\right. \\ $$$$\left.\:\mathrm{Suppose}\:\mathrm{we}\:\mathrm{can}\:\mathrm{list}\:\mathrm{all}\:\mathrm{number}\:\mathrm{in}\:\right]\mathrm{0};\mathrm{1}\left[\right. \\ $$$$\:\mathrm{x}_{\mathrm{1}} =\mathrm{0}.\mathrm{x}_{\mathrm{11}} \mathrm{x}_{\mathrm{12}} \mathrm{x}_{\mathrm{13}} ... \\ $$$$\:\mathrm{x}_{\mathrm{2}} =\mathrm{0}.\mathrm{x}_{\mathrm{21}} \mathrm{x}_{\mathrm{22}} \mathrm{x}_{\mathrm{23}} ... \\ $$$$\:\mathrm{x}_{\mathrm{3}} =\mathrm{0}.\mathrm{x}_{\mathrm{31}} \mathrm{x}_{\mathrm{32}} \mathrm{x}_{\mathrm{33}} ... \\ $$$$..... \\ $$$$\:\mathrm{x}_{\mathrm{ij}} =\mathrm{0},...\mathrm{9} \\ $$$$\:\mathrm{Consider}\:\mathrm{a}=\mathrm{0}.\mathrm{x}_{\mathrm{11}} \mathrm{x}_{\mathrm{22}} \mathrm{x}_{\mathrm{33}} .... \\ $$$$\:\mathrm{construct}\:\mathrm{the}\:\mathrm{number}\:\mathrm{x}=\mathrm{0}.\mathrm{a}_{\mathrm{1}} \mathrm{a}_{\mathrm{2}} \mathrm{a}_{\mathrm{3}} ... \\ $$$$\:\mathrm{with}\:\mathrm{a}_{\mathrm{i}} \neq\mathrm{x}_{\mathrm{ii}} \:\left(\mathrm{and}\:\mathrm{a}_{\mathrm{i}} \neq\mathrm{9}\right) \\ $$$$\:\mathrm{then}\:\mathrm{x}\neq\mathrm{x}_{\mathrm{1}} \:;\:\mathrm{x}\neq\mathrm{x}_{\mathrm{2}} .... \\ $$$$\:\mathrm{then}\:\mathrm{x}\:\mathrm{is}\:\mathrm{not}\:\mathrm{in}\:\mathrm{the}\:\mathrm{list} \\ $$$$\:\mathrm{hence}\:\mathbb{R}\:\mathrm{is}\:\mathrm{uncountable}. \\ $$
Answered by mathmax by abdo last updated on 09/Sep/20
![nature of Σ_(n=2) ^∞ ((sin(n))/(n(n+1))) we have ∣((sin(n))/(n(n+1)))∣≤(1/(n(n+1)))≤(1/n^2 ) the serie Σ (1/n^2 ) converges ⇒this serie converges nsture of Σ_(n=1) ^∞ (1/(n+(√n))) let f(x) =(1/(x+(√x))) with x≥1 we hsve f^′ (x) =−((1+(1/(2(√x))))/((x+(√x))^2 )) <0 ⇒f is decreazing so this serie hsve nature of ∫_1 ^(+∞) (dx/(x+(√x))) changement (√x)=t give ∫_1 ^(+∞) (dx/(x+(√x))) =∫_1 ^(+∞) ((2tdt)/(t^2 +t)) =2 ∫_1 ^(+∞) (dt/(t+1)) =2lim_(a→+∞) ∫_1 ^a (dt/(t+1)) =2lim_(a→+∞) [ln(t+1)]_1 ^a =2lim_(a→+∞) ln(a+1)−ln2 =+∞ ⇒ this serie is divergent](Q112623.png)
$$\mathrm{nature}\:\mathrm{of}\:\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\frac{\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}\:\mathrm{we}\:\mathrm{have}\:\mid\frac{\mathrm{sin}\left(\mathrm{n}\right)}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}\mid\leqslant\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)}\leqslant\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} } \\ $$$$\mathrm{the}\:\mathrm{serie}\:\Sigma\:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:\mathrm{converges}\:\Rightarrow\mathrm{this}\:\mathrm{serie}\:\mathrm{converges} \\ $$$$\mathrm{nsture}\:\mathrm{of}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}+\sqrt{\mathrm{n}}}\:\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}+\sqrt{\mathrm{x}}}\:\:\mathrm{with}\:\mathrm{x}\geqslant\mathrm{1}\:\mathrm{we}\:\mathrm{hsve} \\ $$$$\mathrm{f}^{'} \left(\mathrm{x}\right)\:=−\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}}}}{\left(\mathrm{x}+\sqrt{\mathrm{x}}\right)^{\mathrm{2}} }\:<\mathrm{0}\:\Rightarrow\mathrm{f}\:\mathrm{is}\:\mathrm{decreazing}\:\mathrm{so}\:\mathrm{this}\:\mathrm{serie}\:\mathrm{hsve}\:\mathrm{nature} \\ $$$$\mathrm{of}\:\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}+\sqrt{\mathrm{x}}}\:\:\mathrm{changement}\:\sqrt{\mathrm{x}}=\mathrm{t}\:\mathrm{give}\: \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dx}}{\mathrm{x}+\sqrt{\mathrm{x}}}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{2tdt}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}}\:=\mathrm{2}\:\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{dt}}{\mathrm{t}+\mathrm{1}}\:=\mathrm{2lim}_{\mathrm{a}\rightarrow+\infty} \int_{\mathrm{1}} ^{\mathrm{a}} \:\frac{\mathrm{dt}}{\mathrm{t}+\mathrm{1}} \\ $$$$=\mathrm{2lim}_{\mathrm{a}\rightarrow+\infty} \left[\mathrm{ln}\left(\mathrm{t}+\mathrm{1}\right)\right]_{\mathrm{1}} ^{\mathrm{a}} \:=\mathrm{2lim}_{\mathrm{a}\rightarrow+\infty} \:\:\mathrm{ln}\left(\mathrm{a}+\mathrm{1}\right)−\mathrm{ln2}\:=+\infty\:\Rightarrow \\ $$$$\mathrm{this}\:\mathrm{serie}\:\mathrm{is}\:\mathrm{divergent}\: \\ $$