
Question and Answers Forum
Question Number 112606 by ajfour last updated on 08/Sep/20
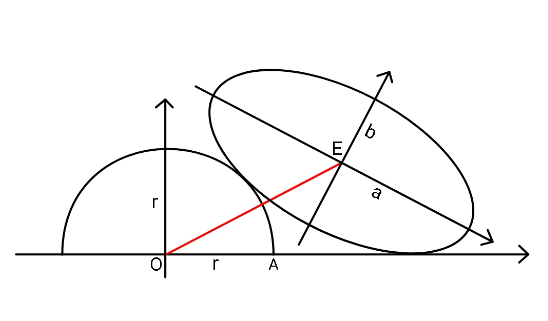
Commented by ajfour last updated on 10/Sep/20

Answered by mr W last updated on 09/Sep/20
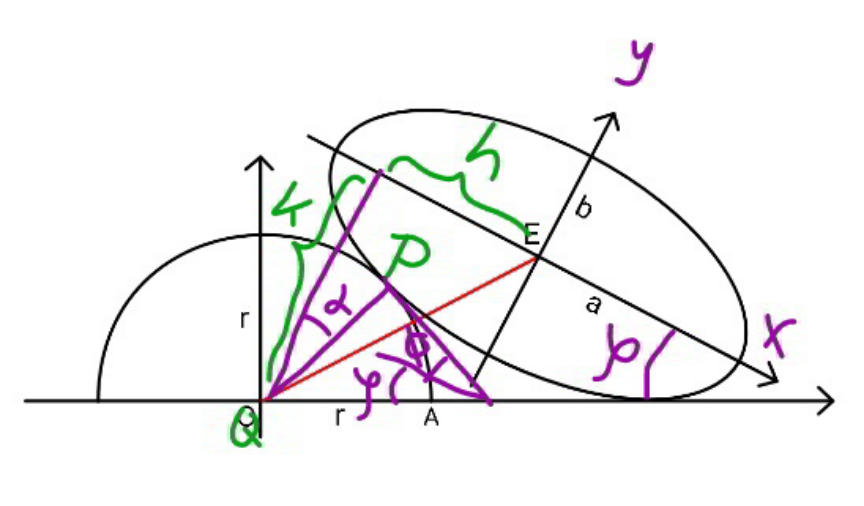
Commented by mr W last updated on 09/Sep/20
![μ=(b/a) ρ=(r/a) η=(h/a) λ=tan ϕ eqn. of QA: y=−k+(x+h)tan ϕ λx−y+(λh−k)=0 λ^2 a^2 +b^2 =(λh−k)^2 ⇒k=λh−(√(λ^2 a^2 +b^2 )) ⇒(k/a)=λη−(√(λ^2 +μ^2 )) P(−a cos θ, −b sin θ) tan φ=(μ/(tan θ)) ϕ+α+((π/2)−ϕ−φ)=(π/2) ⇒α⇒φ −a cos θ=−h+r sin φ ⇒ρ sin φ=η−cos θ −b sin θ=−k+r cos φ ⇒ρ cos φ=λη−(√(λ^2 +μ^2 ))−μ sin θ ⇒tan φ=((η−cos θ)/(λη−(√(λ^2 +μ^2 ))−μ sin θ)) ⇒(μ/(tan θ))=((η−cos θ)/(λη−(√(λ^2 +μ^2 ))−μ sin θ)) (μλ−tan θ)η=μ(√(λ^2 +μ^2 ))−(1−μ^2 )sin θ ⇒η=((μ(√(λ^2 +μ^2 ))−(1−μ^2 )sin θ)/(μλ−tan θ)) ⇒ρ^2 =(η−cos θ)^2 +(λη−(√(λ^2 +μ^2 ))−μ sin θ)^2 x_A =−h+r cos ϕ y_A =−k+r sin ϕ AE^2 =(h−r cos ϕ)^2 +(k−r sin ϕ)^2 Φ=(((AE)/a))^2 =(η−ρ cos ϕ)^2 +(λη−(√(λ^2 +μ^2 ))−ρ sin ϕ)^2 Φ=[((μ(√(λ^2 +μ^2 ))−(1−μ^2 )sin θ)/(μλ−tan θ))−ρ cos ϕ]^2 +[((μλ(√(λ^2 +μ^2 ))−λ(1−μ^2 )sin θ)/(μλ−tan θ))−(√(λ^2 +μ^2 ))−ρ sin ϕ]^2 .....](Q112826.png)
| ||
Question and Answers Forum | ||
Question Number 112606 by ajfour last updated on 08/Sep/20 | ||
 | ||
Commented by ajfour last updated on 10/Sep/20 | ||
 | ||
Answered by mr W last updated on 09/Sep/20 | ||
 | ||
Commented by mr W last updated on 09/Sep/20 | ||
![μ=(b/a) ρ=(r/a) η=(h/a) λ=tan ϕ eqn. of QA: y=−k+(x+h)tan ϕ λx−y+(λh−k)=0 λ^2 a^2 +b^2 =(λh−k)^2 ⇒k=λh−(√(λ^2 a^2 +b^2 )) ⇒(k/a)=λη−(√(λ^2 +μ^2 )) P(−a cos θ, −b sin θ) tan φ=(μ/(tan θ)) ϕ+α+((π/2)−ϕ−φ)=(π/2) ⇒α⇒φ −a cos θ=−h+r sin φ ⇒ρ sin φ=η−cos θ −b sin θ=−k+r cos φ ⇒ρ cos φ=λη−(√(λ^2 +μ^2 ))−μ sin θ ⇒tan φ=((η−cos θ)/(λη−(√(λ^2 +μ^2 ))−μ sin θ)) ⇒(μ/(tan θ))=((η−cos θ)/(λη−(√(λ^2 +μ^2 ))−μ sin θ)) (μλ−tan θ)η=μ(√(λ^2 +μ^2 ))−(1−μ^2 )sin θ ⇒η=((μ(√(λ^2 +μ^2 ))−(1−μ^2 )sin θ)/(μλ−tan θ)) ⇒ρ^2 =(η−cos θ)^2 +(λη−(√(λ^2 +μ^2 ))−μ sin θ)^2 x_A =−h+r cos ϕ y_A =−k+r sin ϕ AE^2 =(h−r cos ϕ)^2 +(k−r sin ϕ)^2 Φ=(((AE)/a))^2 =(η−ρ cos ϕ)^2 +(λη−(√(λ^2 +μ^2 ))−ρ sin ϕ)^2 Φ=[((μ(√(λ^2 +μ^2 ))−(1−μ^2 )sin θ)/(μλ−tan θ))−ρ cos ϕ]^2 +[((μλ(√(λ^2 +μ^2 ))−λ(1−μ^2 )sin θ)/(μλ−tan θ))−(√(λ^2 +μ^2 ))−ρ sin ϕ]^2 .....](Q112826.png) | ||