Question Number 112655 by mathdave last updated on 09/Sep/20
$${prove}\:{that}\: \\ $$$$\infty!=\sqrt{\mathrm{2}\pi} \\ $$
Commented by MJS_new last updated on 09/Sep/20
$$\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{people}\:\mathrm{with}\:\mathrm{less}\:\mathrm{knowledge}\:\mathrm{to} \\ $$$$\mathrm{understand}\:\mathrm{this},\:\mathrm{you}\:\mathrm{should}\:\mathrm{explain}\:\mathrm{the} \\ $$$$\mathrm{background}\:\mathrm{of}\:\mathrm{it}.\:\mathrm{this}\:\mathrm{would}\:\mathrm{be}\:\mathrm{helpful}.\:\mathrm{show} \\ $$$$\mathrm{us}\:\mathrm{why}\:\mathrm{the}\:\mathrm{faculty}\:\mathrm{of}\:\mathrm{infinity}\:\mathrm{has}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{value}\:\mathrm{as}\:\mathrm{the}\:\mathrm{Gaussian}\:\mathrm{integral} \\ $$
Commented by mathdave last updated on 09/Sep/20
$${alright}\:{sir} \\ $$
Answered by mathdave last updated on 09/Sep/20
![solution since η(s)=Σ_(k=1) ^∞ (−1)^(k+1) k^(−s) =(1−2^(1−s) )ζ(s) η^′ (s)=Σ_(k=1) ^∞ (−1)^k ((lnk)/k^s )=ζ^′ (s)(1−2^(1−s) )+ζ(s)2ln2 η^′ (0)=Σ_(k=1) ^∞ (−1)^k lnk=−ln(1)+ln(2)−ln(3)+−−−− η^′ (0)=ln((π/2))−η^′ (0)[walli′s product] η^′ (0)=(1/2)ln((π/2))=ln((√(π/2))).........(1) again η^′ (0)=−ζ^′ (0)+ζ(0)2ln2=−[η^′ (0)−ln(π)]−ln2 2η^′ (0)=ln((π/2)) η^′ (0)=(1/2)ln((π/2))=ln((√(π/2))).........(2) but ln((√(π/2)))=ln(Π_(k=1) k)−ln2 ln((√(π/2)))=ln(∞!)−ln2 ln(∞!)=ln2+ln((√(π/2))) ln(∞!)=ln (2(√(π/2)))=ln((√(2π))) ln(∞!)=ln((√(2π))) ∵ ∞!=(√(2π)) Q.E.D by mathdave(09/09/2020)](Q112698.png)
$${solution}\: \\ $$$${since} \\ $$$$\eta\left({s}\right)=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} {k}^{−{s}} =\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{s}} \right)\zeta\left({s}\right) \\ $$$$\eta^{'} \left({s}\right)=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \frac{\mathrm{ln}{k}}{{k}^{{s}} }=\zeta^{'} \left({s}\right)\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−{s}} \right)+\zeta\left({s}\right)\mathrm{2ln2} \\ $$$$\eta^{'} \left(\mathrm{0}\right)=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \mathrm{ln}{k}=−\mathrm{ln}\left(\mathrm{1}\right)+\mathrm{ln}\left(\mathrm{2}\right)−\mathrm{ln}\left(\mathrm{3}\right)+−−−− \\ $$$$\eta^{'} \left(\mathrm{0}\right)=\mathrm{ln}\left(\frac{\pi}{\mathrm{2}}\right)−\eta^{'} \left(\mathrm{0}\right)\left[{walli}'{s}\:{product}\right] \\ $$$$\eta^{'} \left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{ln}\left(\sqrt{\frac{\pi}{\mathrm{2}}}\right).........\left(\mathrm{1}\right) \\ $$$${again} \\ $$$$\eta^{'} \left(\mathrm{0}\right)=−\zeta^{'} \left(\mathrm{0}\right)+\zeta\left(\mathrm{0}\right)\mathrm{2ln2}=−\left[\eta^{'} \left(\mathrm{0}\right)−\mathrm{ln}\left(\pi\right)\right]−\mathrm{ln2} \\ $$$$\mathrm{2}\eta^{'} \left(\mathrm{0}\right)=\mathrm{ln}\left(\frac{\pi}{\mathrm{2}}\right) \\ $$$$\eta^{'} \left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{ln}\left(\sqrt{\frac{\pi}{\mathrm{2}}}\right).........\left(\mathrm{2}\right) \\ $$$${but}\:\mathrm{ln}\left(\sqrt{\frac{\pi}{\mathrm{2}}}\right)=\mathrm{ln}\left(\underset{{k}=\mathrm{1}} {\prod}{k}\right)−\mathrm{ln2} \\ $$$$\mathrm{ln}\left(\sqrt{\frac{\pi}{\mathrm{2}}}\right)=\mathrm{ln}\left(\infty!\right)−\mathrm{ln2} \\ $$$$\mathrm{ln}\left(\infty!\right)=\mathrm{ln2}+\mathrm{ln}\left(\sqrt{\frac{\pi}{\mathrm{2}}}\right) \\ $$$$\mathrm{ln}\left(\infty!\right)=\mathrm{ln}\:\left(\mathrm{2}\sqrt{\frac{\pi}{\mathrm{2}}}\right)=\mathrm{ln}\left(\sqrt{\mathrm{2}\pi}\right) \\ $$$$\mathrm{ln}\left(\infty!\right)=\mathrm{ln}\left(\sqrt{\mathrm{2}\pi}\right) \\ $$$$\because\:\infty!=\sqrt{\mathrm{2}\pi}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{Q}.{E}.{D} \\ $$$${by}\:{mathdave}\left(\mathrm{09}/\mathrm{09}/\mathrm{2020}\right) \\ $$$$ \\ $$
Commented by Her_Majesty last updated on 09/Sep/20
![show that X^(⟨7⟩) ⇒^! (X−1)^(⟨−3⟩) proof: X^7 ⊂X^(⟨7∣−9⟩) ⊃(X+1)^(⟨−3∣−5∣=7⟩) but (X+1)^(⟨−3∣−5∣=7⟩) =(X−5)^(⟨−3∣−5∣=7⟩) and (X−5)^(⟨−3∣−5∣=7⟩) ⊂(X−6)^(⟨7∣−9⟩) ⊃(X−6)^(⟨7⟩) but we know (x+u) ⇒^! (x+v) ⇔ v= { ((u+5)),((u−7)) :} (Beck−Runnel−Axiom) ⇒ (x−6) ⇒^! (x−1) ⇒ ⇒ (X−6)^(⟨7⟩) ⇒^! (X−1)^(⟨−3⟩) but we have shown (X−6)^(⟨7⟩) ⊂(X−6)^(⟨7∣−9⟩) ⊃(X−5)^(⟨−3∣−5∣−^(2o) 7⟩) = =(X+1)^(⟨−3∣−5∣=7⟩) ⊂X^(⟨7∣−9⟩) ⊃X^(⟨7⟩) ⇒ ⇒ X^(⟨7⟩) ⇒^! (X−1)^(⟨−3⟩) q.e.d. [b.t.w. because of the Axioms of Inversion (X+u)^(⟨−3∣7⟩) =(X+v)^(⟨6⟩) with v= { ((u+3)),((u−9)) :} we also showed that X^(⟨7⟩) ⇒^! (X+2) which is essential to Simon′s Approach]](Q112718.png)
$${show}\:{that}\:{X}^{\langle\mathrm{7}\rangle} \:\overset{!} {\Rightarrow}\:\left({X}−\mathrm{1}\right)^{\langle−\mathrm{3}\rangle} \\ $$$${proof}: \\ $$$${X}^{\mathrm{7}} \subset{X}^{\langle\mathrm{7}\mid−\mathrm{9}\rangle} \supset\left({X}+\mathrm{1}\right)^{\langle−\mathrm{3}\mid−\mathrm{5}\mid=\mathrm{7}\rangle} \\ $$$${but}\:\left({X}+\mathrm{1}\right)^{\langle−\mathrm{3}\mid−\mathrm{5}\mid=\mathrm{7}\rangle} =\left({X}−\mathrm{5}\right)^{\langle−\mathrm{3}\mid−\mathrm{5}\mid=\mathrm{7}\rangle} \\ $$$${and}\:\left({X}−\mathrm{5}\right)^{\langle−\mathrm{3}\mid−\mathrm{5}\mid=\mathrm{7}\rangle} \subset\left({X}−\mathrm{6}\right)^{\langle\mathrm{7}\mid−\mathrm{9}\rangle} \supset\left({X}−\mathrm{6}\right)^{\langle\mathrm{7}\rangle} \\ $$$${but}\:{we}\:{know}\:\left({x}+{u}\right)\:\overset{!} {\Rightarrow}\:\left({x}+{v}\right)\:\Leftrightarrow\:{v}=\begin{cases}{{u}+\mathrm{5}}\\{{u}−\mathrm{7}}\end{cases} \\ $$$$\left({Beck}−{Runnel}−{Axiom}\right) \\ $$$$\Rightarrow\:\left({x}−\mathrm{6}\right)\:\overset{!} {\Rightarrow}\:\left({x}−\mathrm{1}\right)\:\Rightarrow \\ $$$$\Rightarrow\:\left({X}−\mathrm{6}\right)^{\langle\mathrm{7}\rangle} \:\overset{!} {\Rightarrow}\:\left({X}−\mathrm{1}\right)^{\langle−\mathrm{3}\rangle} \\ $$$${but}\:{we}\:{have}\:{shown}\: \\ $$$$\left({X}−\mathrm{6}\right)^{\langle\mathrm{7}\rangle} \subset\left({X}−\mathrm{6}\right)^{\langle\mathrm{7}\mid−\mathrm{9}\rangle} \supset\left({X}−\mathrm{5}\right)^{\langle−\mathrm{3}\mid−\mathrm{5}\mid\overset{\mathrm{2}{o}} {−}\mathrm{7}\rangle} = \\ $$$$=\left({X}+\mathrm{1}\right)^{\langle−\mathrm{3}\mid−\mathrm{5}\mid=\mathrm{7}\rangle} \subset{X}^{\langle\mathrm{7}\mid−\mathrm{9}\rangle} \supset{X}^{\langle\mathrm{7}\rangle} \:\Rightarrow \\ $$$$\Rightarrow\:{X}^{\langle\mathrm{7}\rangle} \:\overset{!} {\Rightarrow}\:\left({X}−\mathrm{1}\right)^{\langle−\mathrm{3}\rangle} \:{q}.{e}.{d}. \\ $$$$ \\ $$$$\left[{b}.{t}.{w}.\:{because}\:{of}\:{the}\:{Axioms}\:{of}\:{Inversion}\right. \\ $$$$\left({X}+{u}\right)^{\langle−\mathrm{3}\mid\mathrm{7}\rangle} =\left({X}+{v}\right)^{\langle\mathrm{6}\rangle} \:{with}\:{v}=\begin{cases}{{u}+\mathrm{3}}\\{{u}−\mathrm{9}}\end{cases} \\ $$$${we}\:{also}\:{showed}\:{that}\:{X}^{\langle\mathrm{7}\rangle} \:\overset{!} {\Rightarrow}\:\left({X}+\mathrm{2}\right)\:{which} \\ $$$$\left.{is}\:{essential}\:{to}\:{Simon}'{s}\:{Approach}\right] \\ $$
Commented by Her_Majesty last updated on 09/Sep/20
![(1) find all possible sources of (X−1)^(⟨+5⟩) [super easy] (2) find possible sources of (a) (X−3)^(⟨+5∣−7⟩) and (b) (X+4)^(⟨−5∣−7⟩) and their center angles [hard]](Q112722.png)
$$\left(\mathrm{1}\right)\:{find}\:{all}\:{possible}\:{sources}\:{of}\:\left({X}−\mathrm{1}\right)^{\langle+\mathrm{5}\rangle} \\ $$$$\:\:\:\:\:\:\:\:\left[{super}\:{easy}\right] \\ $$$$\left(\mathrm{2}\right)\:{find}\:{possible}\:{sources}\:{of} \\ $$$$\left({a}\right)\:\left({X}−\mathrm{3}\right)^{\langle+\mathrm{5}\mid−\mathrm{7}\rangle} \:{and}\:\left({b}\right)\:\left({X}+\mathrm{4}\right)^{\langle−\mathrm{5}\mid−\mathrm{7}\rangle} \\ $$$${and}\:{their}\:{center}\:{angles}\:\left[{hard}\right] \\ $$
Commented by MJS_new last updated on 09/Sep/20
$$\mathrm{what}'\mathrm{s}\:\mathrm{this}??? \\ $$
Commented by 1549442205PVT last updated on 09/Sep/20
$$\mathrm{Please},\mathrm{Sir}\:\mathrm{Mathdave}\:\mathrm{can}\:\mathrm{explain}\: \\ $$$$\:\mathrm{at}\:\mathrm{tenth}\:\mathrm{line} \\ $$$$\mathrm{ln}\sqrt{\frac{\pi}{\mathrm{2}}}=\mathrm{ln}\left(\underset{\mathrm{k}} {\Pi}\mathrm{k}\right)−\mathrm{ln2} \\ $$$$\underset{\mathrm{k}} {\prod}\mathrm{k}\:\mathrm{is}\:\mathrm{an}\:\mathrm{infinite}\:\mathrm{value}\:\mathrm{while}\:\sqrt{\pi}\:<\mathrm{2} \\ $$$$\left(\mathrm{Math}\:\mathrm{is}\:\mathrm{beautiful}\:\mathrm{because}\:\mathrm{of}\:\mathrm{its}\right. \\ $$$$\left.\mathrm{precision}\right) \\ $$
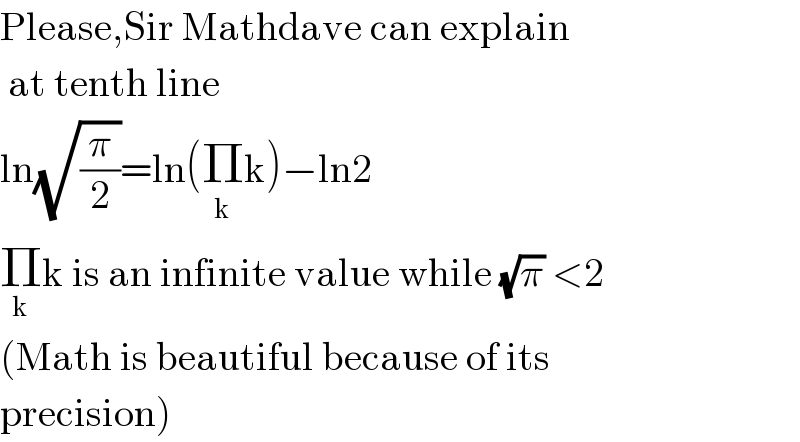
Commented by Tawa11 last updated on 06/Sep/21
$$\mathrm{great}\:\mathrm{sir} \\ $$