Question Number 112697 by mnjuly1970 last updated on 09/Sep/20
$$\:\:\:\:\:....{calculus}... \\ $$$${please}\:\:{prove}\:: \\ $$$$ \\ $$$$\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\varphi} \right)^{\varphi} }{dx}\:=\mathrm{1} \\ $$$$\:\varphi::\:\:{golden}\:\:{ratio}\:... \\ $$
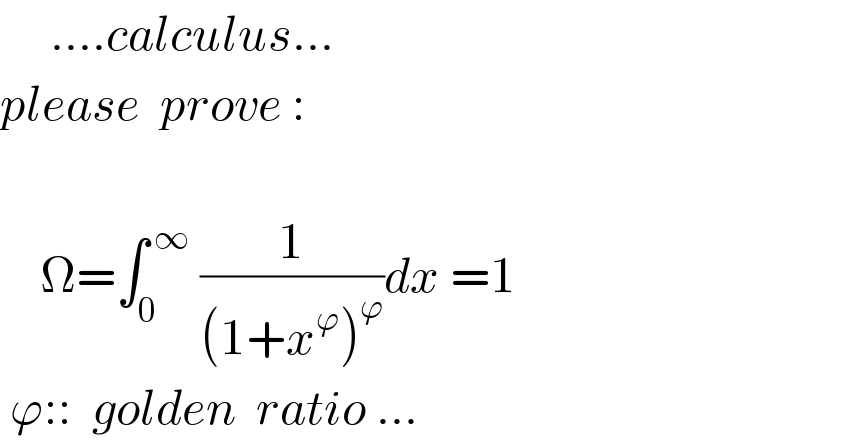
Commented by mathdave last updated on 09/Sep/20
$${this}\:{is}\:{simple}\:{nah} \\ $$
Commented by MJS_new last updated on 09/Sep/20
$$\mathrm{I}\:\mathrm{haven}'\mathrm{t}\:\mathrm{found}\:\mathrm{it}\:\mathrm{yet}\:\mathrm{but}\:\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{play} \\ $$$$\mathrm{around}\:\mathrm{with}\:\mathrm{the}\:\mathrm{fact} \\ $$$$\frac{\mathrm{1}}{\varphi}=\varphi−\mathrm{1}\:\mathrm{and}\:\varphi^{\mathrm{2}} =\varphi+\mathrm{1} \\ $$
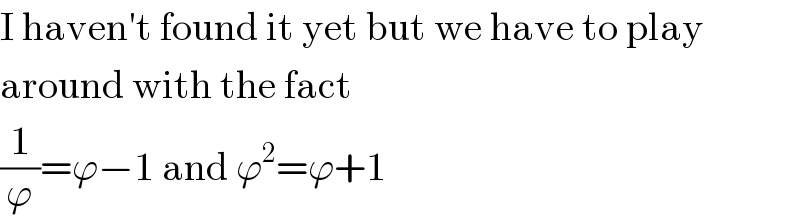
Commented by mnjuly1970 last updated on 09/Sep/20
$${you}\:{are}\:{right}.. \\ $$
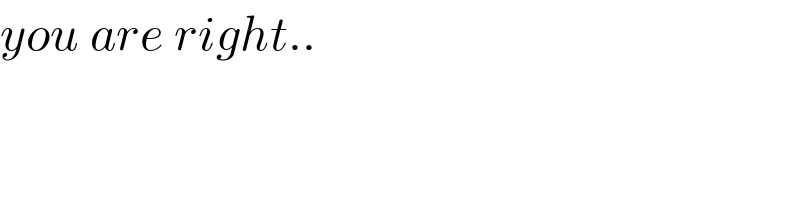
Answered by MJS_new last updated on 09/Sep/20
![trying “reverse method” (d/dx)[f(x)(1+x^ϕ )^(1−ϕ) ]= =f′(x)(1+x^ϕ )^(1−ϕ) +(ϕ−ϕ^2 )f(x)(x^(ϕ−1) /((1+x^ϕ )^ϕ ))= =((f′(x)(1+x^ϕ )+(ϕ−ϕ^2 )f(x)x^(ϕ−1) )/((1+x^ϕ )^(ϕ ) )) putting f(x)=x we get (((1+ϕ−ϕ^2 )x^ϕ +1)/((1+x^ϕ )^ϕ )) but 1+ϕ−ϕ^2 =0 ⇒ ∫(dx/((1+x^ϕ )^ϕ ))=(x/((1+x^ϕ )^(ϕ−1) ))+C=(x/((1+x^ϕ )^(1/ϕ) ))+C ∫_0 ^∞ (dx/((1+x^ϕ )^ϕ ))=lim_(x→∞) (x/((1+x^ϕ )^(1/ϕ) )) =1](Q112745.png)
$$\mathrm{trying}\:``\mathrm{reverse}\:\mathrm{method}'' \\ $$$$\frac{{d}}{{dx}}\left[{f}\left({x}\right)\left(\mathrm{1}+{x}^{\varphi} \right)^{\mathrm{1}−\varphi} \right]= \\ $$$$={f}'\left({x}\right)\left(\mathrm{1}+{x}^{\varphi} \right)^{\mathrm{1}−\varphi} +\left(\varphi−\varphi^{\mathrm{2}} \right){f}\left({x}\right)\frac{{x}^{\varphi−\mathrm{1}} }{\left(\mathrm{1}+{x}^{\varphi} \right)^{\varphi} }= \\ $$$$=\frac{{f}'\left({x}\right)\left(\mathrm{1}+{x}^{\varphi} \right)+\left(\varphi−\varphi^{\mathrm{2}} \right){f}\left({x}\right){x}^{\varphi−\mathrm{1}} }{\left(\mathrm{1}+{x}^{\varphi} \right)^{\varphi\:} } \\ $$$$\mathrm{putting}\:{f}\left({x}\right)={x}\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\left(\mathrm{1}+\varphi−\varphi^{\mathrm{2}} \right){x}^{\varphi} +\mathrm{1}}{\left(\mathrm{1}+{x}^{\varphi} \right)^{\varphi} } \\ $$$$\mathrm{but}\:\mathrm{1}+\varphi−\varphi^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\int\frac{{dx}}{\left(\mathrm{1}+{x}^{\varphi} \right)^{\varphi} }=\frac{{x}}{\left(\mathrm{1}+{x}^{\varphi} \right)^{\varphi−\mathrm{1}} }+{C}=\frac{{x}}{\left(\mathrm{1}+{x}^{\varphi} \right)^{\mathrm{1}/\varphi} }+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dx}}{\left(\mathrm{1}+{x}^{\varphi} \right)^{\varphi} }=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{x}}{\left(\mathrm{1}+{x}^{\varphi} \right)^{\mathrm{1}/\varphi} }\:=\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 09/Sep/20
$${nice}\:{method}.. \\ $$
Commented by MJS_new last updated on 09/Sep/20
$$\mathrm{it}\:\mathrm{works}\:\mathrm{only}\:\mathrm{sometimes}... \\ $$
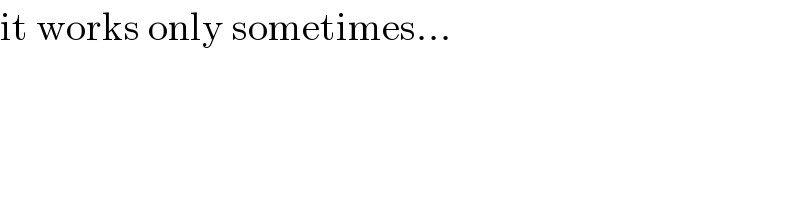
Answered by ajfour last updated on 09/Sep/20
![I=∫(dx/([1+x(x^(1/ϕ) )]^ϕ )) =∫(dx/(x(x^(−1/ϕ) +x)^ϕ )) let x=e^t ⇒ (dx/x)=dt I=∫_(−∞) ^( ∞) (dt/((e^(−t((1/ϕ))) +e^t )^ϕ )) but (1/ϕ)=ϕ−1 , so I=∫(dt/(((e^t /e^(ϕt) )+e^t )^ϕ )) = ∫_(−∞) ^( ∞) ((e^(−ϕt) dt)/((e^(−ϕt) +1)^ϕ )) let e^(−ϕt) +1=z ⇒ e^(−ϕt) dt = −(dz/ϕ) I=−(1/ϕ)∫_∞ ^( 1) z^(−ϕ) dz I=(1/(ϕ(ϕ−1)))[z^(−ϕ+1) ]_∞ ^1 I = (((ϕ−1)/(ϕ−1)))(1−0) = 1 ★.................................★](Q112761.png)
$${I}=\int\frac{{dx}}{\left[\mathrm{1}+{x}\left({x}^{\mathrm{1}/\varphi} \right)\right]^{\varphi} } \\ $$$$\:\:=\int\frac{{dx}}{{x}\left({x}^{−\mathrm{1}/\varphi} +{x}\right)^{\varphi} } \\ $$$$\:{let}\:{x}={e}^{{t}} \:\:\:\Rightarrow\:\:\frac{{dx}}{{x}}={dt} \\ $$$$\:{I}=\int_{−\infty} ^{\:\:\infty} \frac{{dt}}{\left({e}^{−{t}\left(\frac{\mathrm{1}}{\varphi}\right)} +{e}^{{t}} \right)^{\varphi} } \\ $$$$\:\:{but}\:\:\frac{\mathrm{1}}{\varphi}=\varphi−\mathrm{1}\:\:\:,\:\:{so} \\ $$$${I}=\int\frac{{dt}}{\left(\frac{{e}^{{t}} }{{e}^{\varphi{t}} }+{e}^{{t}} \right)^{\varphi} }\:=\:\int_{−\infty} ^{\:\:\infty} \frac{{e}^{−\varphi{t}} {dt}}{\left({e}^{−\varphi{t}} +\mathrm{1}\right)^{\varphi} } \\ $$$${let}\:\:{e}^{−\varphi{t}} +\mathrm{1}={z} \\ $$$$\Rightarrow\:\:\:\:{e}^{−\varphi{t}} {dt}\:=\:−\frac{{dz}}{\varphi} \\ $$$${I}=−\frac{\mathrm{1}}{\varphi}\int_{\infty} ^{\:\mathrm{1}} {z}^{−\varphi} {dz}\: \\ $$$${I}=\frac{\mathrm{1}}{\varphi\left(\varphi−\mathrm{1}\right)}\left[{z}^{−\varphi+\mathrm{1}} \right]_{\infty} ^{\mathrm{1}} \\ $$$${I}\:=\:\left(\frac{\varphi−\mathrm{1}}{\varphi−\mathrm{1}}\right)\left(\mathrm{1}−\mathrm{0}\right)\:=\:\mathrm{1}\:\: \\ $$$$\bigstar.................................\bigstar \\ $$$$\:\: \\ $$
Commented by mnjuly1970 last updated on 09/Sep/20
$${nice}\:{very}\:{nice}\:\:{mr}\:{ajfour}\:. \\ $$$${thank}\:{you}\:{very}\:{much}. \\ $$
Answered by mnjuly1970 last updated on 09/Sep/20
![solution. we know that:: ∫_0 ^( ∞) (x^(p−1) /((1+x)^(p+q) ))dx = ((Γ(p)Γ(q))/(Γ(p+q))) x^ϕ =t ⇒dx =(1/ϕ)t^((1/ϕ) −1) Ω =(1/ϕ) ∫_0 ^( ∞) (t^((1/ϕ) −1) /((1+t)^ϕ )) dt = (1/ϕ)[((Γ((1/ϕ))Γ(ϕ−(1/ϕ)))/(Γ(ϕ )))] we know that : ϕ^2 =ϕ+1⇒ϕ=1+(1/ϕ) ∴ Ω =(1/ϕ)(((Γ((1/ϕ)))/(Γ(ϕ))))=((Γ(1+(1/ϕ)))/(Γ(ϕ))) =((Γ(ϕ))/(Γ(ϕ))) =1 ✓ ...m.n...](Q112762.png)
$${solution}. \\ $$$${we}\:{know}\:{that}:: \\ $$$$\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{{x}^{{p}−\mathrm{1}} }{\left(\mathrm{1}+{x}\right)^{{p}+{q}} }{dx}\:=\:\:\frac{\Gamma\left({p}\right)\Gamma\left({q}\right)}{\Gamma\left({p}+{q}\right)} \\ $$$$\:\:{x}^{\varphi} \:={t}\:\Rightarrow{dx}\:=\frac{\mathrm{1}}{\varphi}{t}^{\frac{\mathrm{1}}{\varphi}\:−\mathrm{1}} \\ $$$$\:\:\Omega\:=\frac{\mathrm{1}}{\varphi}\:\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{\frac{\mathrm{1}}{\varphi}\:−\mathrm{1}} }{\left(\mathrm{1}+{t}\right)^{\varphi} }\:{dt}\:=\:\frac{\mathrm{1}}{\varphi}\left[\frac{\Gamma\left(\frac{\mathrm{1}}{\varphi}\right)\Gamma\left(\varphi−\frac{\mathrm{1}}{\varphi}\right)}{\Gamma\left(\varphi\:\right)}\right] \\ $$$$\:\:\:\:{we}\:{know}\:{that}\::\:\:\varphi^{\mathrm{2}} =\varphi+\mathrm{1}\Rightarrow\varphi=\mathrm{1}+\frac{\mathrm{1}}{\varphi} \\ $$$$\therefore\:\Omega\:=\frac{\mathrm{1}}{\varphi}\left(\frac{\Gamma\left(\frac{\mathrm{1}}{\varphi}\right)}{\Gamma\left(\varphi\right)}\right)=\frac{\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\varphi}\right)}{\Gamma\left(\varphi\right)}\:=\frac{\Gamma\left(\varphi\right)}{\Gamma\left(\varphi\right)}\: \\ $$$$\:=\mathrm{1}\:\checkmark \\ $$$$\:\:\:\:\:\:\:...{m}.{n}... \\ $$$$\: \\ $$
Commented by Tawa11 last updated on 06/Sep/21
$$\mathrm{great}\:\mathrm{sir} \\ $$