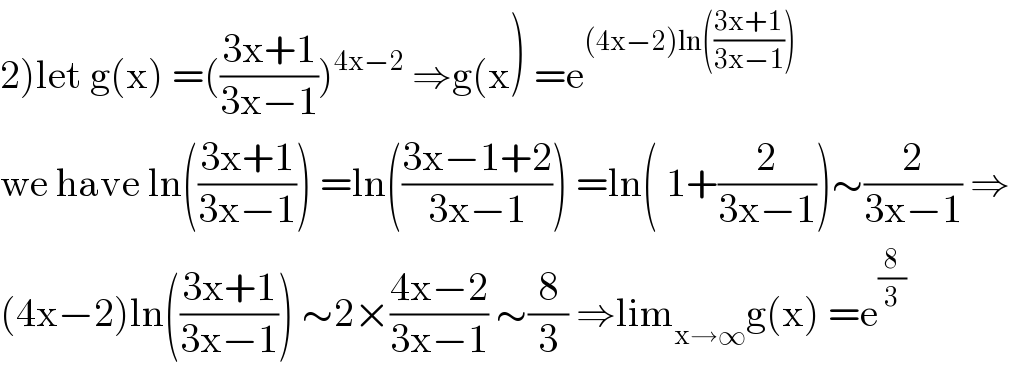Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 112863 by bemath last updated on 10/Sep/20

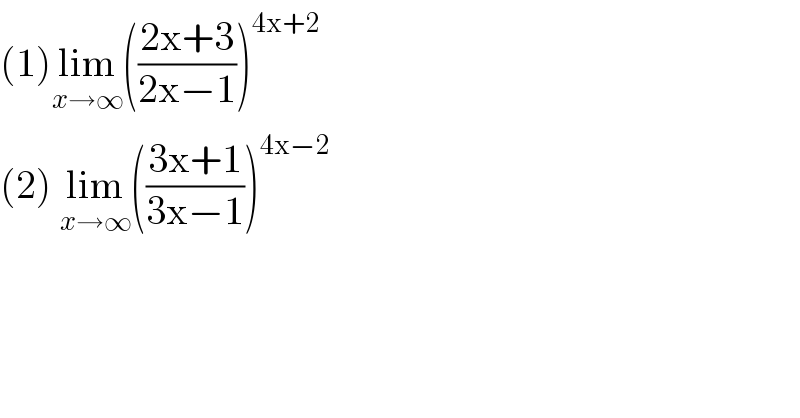
(1)lim_(x→∞) (((2x+3)/(2x−1)))^(4x+2) (2) lim_(x→∞) (((3x+1)/(3x−1)))^(4x−2)

$$\left(\mathrm{1}\right)\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{2x}−\mathrm{1}}\right)^{\mathrm{4x}+\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{3x}+\mathrm{1}}{\mathrm{3x}−\mathrm{1}}\right)^{\mathrm{4x}−\mathrm{2}} \\ $$

Commented by bobhans last updated on 22/Sep/20

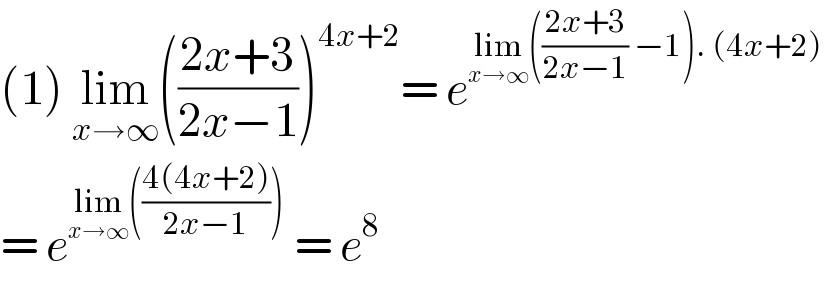
(1) lim_(x→∞) (((2x+3)/(2x−1)))^(4x+2) = e^(lim_(x→∞) (((2x+3)/(2x−1)) −1). (4x+2)) = e^(lim_(x→∞) (((4(4x+2))/(2x−1)))) = e^8

$$\left(\mathrm{1}\right)\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}{x}+\mathrm{3}}{\mathrm{2}{x}−\mathrm{1}}\right)^{\mathrm{4}{x}+\mathrm{2}} =\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}{x}+\mathrm{3}}{\mathrm{2}{x}−\mathrm{1}}\:−\mathrm{1}\right).\:\left(\mathrm{4}{x}+\mathrm{2}\right)} \\ $$$$=\:{e}^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{4}\left(\mathrm{4}{x}+\mathrm{2}\right)}{\mathrm{2}{x}−\mathrm{1}}\right)} \:=\:{e}^{\mathrm{8}} \\ $$

Answered by bobhans last updated on 10/Sep/20

lim_(x→∞) (((3x−1+2)/(3x−1)))^(4x−2) = lim_(x→∞) (1+(2/(3x−1)))^(4x−2) let u = (2/(3x−1)), u→0 and 3x−1 = (2/u) x = ((2+u)/(3u)) . then lim_(u→0) (1+u)^(((4u+8)/(3u))−2) lim_(u→0) [(1+u)^(1/u) ]^((8−2u)/3) = e^(lim_(u→0) (((8−2u)/3))) = e^(8/3)

$$\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{3x}−\mathrm{1}+\mathrm{2}}{\mathrm{3x}−\mathrm{1}}\right)^{\mathrm{4x}−\mathrm{2}} \:=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3x}−\mathrm{1}}\right)^{\mathrm{4x}−\mathrm{2}} \\ $$$$\mathrm{let}\:\mathrm{u}\:=\:\frac{\mathrm{2}}{\mathrm{3x}−\mathrm{1}},\:\mathrm{u}\rightarrow\mathrm{0}\:\mathrm{and}\:\mathrm{3x}−\mathrm{1}\:=\:\frac{\mathrm{2}}{\mathrm{u}}\: \\ $$$$\mathrm{x}\:=\:\frac{\mathrm{2}+\mathrm{u}}{\mathrm{3u}}\:.\:\mathrm{then}\:\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\mathrm{u}\right)^{\frac{\mathrm{4u}+\mathrm{8}}{\mathrm{3u}}−\mathrm{2}} \\ $$$$\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}+\mathrm{u}\right)^{\frac{\mathrm{1}}{\mathrm{u}}} \right]^{\frac{\mathrm{8}−\mathrm{2u}}{\mathrm{3}}} =\:\mathrm{e}^{\underset{\mathrm{u}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{8}−\mathrm{2u}}{\mathrm{3}}\right)} \:=\:\mathrm{e}^{\frac{\mathrm{8}}{\mathrm{3}}} \\ $$

Answered by bobhans last updated on 10/Sep/20

lim_(x→∞) (((2x−1+4)/(2x−1)))^(4x+2) =lim_(x→∞) (1+(4/(2x−1)))^(4x+2) let q = (4/(2x−1))→x = ((4+q)/(2q)) lim_(q→0) [(1+q)^(((8+2q)/q)+2) ]= lim_(q→0) [(1+q)^(1/q) ]^(4q+8) = e^(lim_(q→0) (4q+8)) = e^8

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{2x}−\mathrm{1}+\mathrm{4}}{\mathrm{2x}−\mathrm{1}}\right)^{\mathrm{4x}+\mathrm{2}} =\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{2x}−\mathrm{1}}\right)^{\mathrm{4x}+\mathrm{2}} \\ $$$$\mathrm{let}\:\mathrm{q}\:=\:\frac{\mathrm{4}}{\mathrm{2x}−\mathrm{1}}\rightarrow\mathrm{x}\:=\:\frac{\mathrm{4}+\mathrm{q}}{\mathrm{2q}} \\ $$$$\underset{\mathrm{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}+\mathrm{q}\right)^{\frac{\mathrm{8}+\mathrm{2q}}{\mathrm{q}}+\mathrm{2}} \right]=\:\underset{\mathrm{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}+\mathrm{q}\right)^{\frac{\mathrm{1}}{\mathrm{q}}} \right]^{\mathrm{4q}+\mathrm{8}} \\ $$$$=\:\mathrm{e}^{\underset{\mathrm{q}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{4q}+\mathrm{8}\right)} =\:\mathrm{e}^{\mathrm{8}} \\ $$

Answered by mathmax by abdo last updated on 10/Sep/20

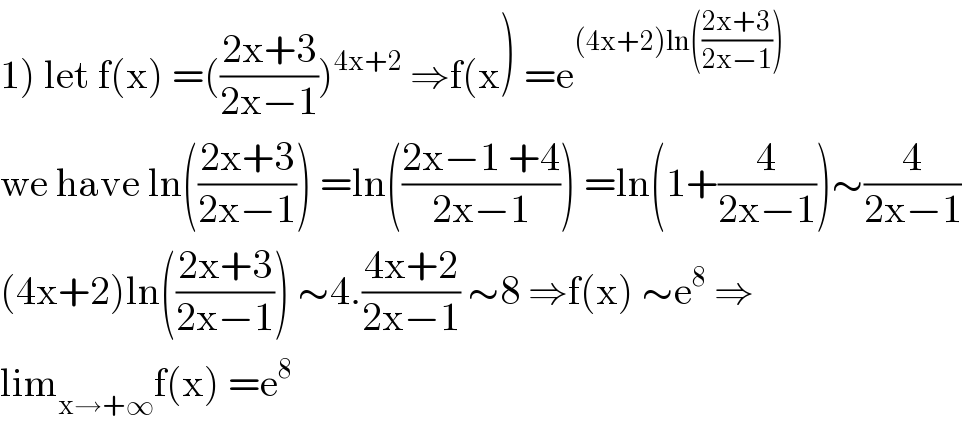
1) let f(x) =(((2x+3)/(2x−1)))^(4x+2) ⇒f(x) =e^((4x+2)ln(((2x+3)/(2x−1)))) we have ln(((2x+3)/(2x−1))) =ln(((2x−1 +4)/(2x−1))) =ln(1+(4/(2x−1)))∼(4/(2x−1)) (4x+2)ln(((2x+3)/(2x−1))) ∼4.((4x+2)/(2x−1)) ∼8 ⇒f(x) ∼e^8 ⇒ lim_(x→+∞) f(x) =e^8

$$\left.\mathrm{1}\right)\:\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{2x}−\mathrm{1}}\right)^{\mathrm{4x}+\mathrm{2}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\left(\mathrm{4x}+\mathrm{2}\right)\mathrm{ln}\left(\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{2x}−\mathrm{1}}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{ln}\left(\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{2x}−\mathrm{1}}\right)\:=\mathrm{ln}\left(\frac{\mathrm{2x}−\mathrm{1}\:+\mathrm{4}}{\mathrm{2x}−\mathrm{1}}\right)\:=\mathrm{ln}\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{2x}−\mathrm{1}}\right)\sim\frac{\mathrm{4}}{\mathrm{2x}−\mathrm{1}} \\ $$$$\left(\mathrm{4x}+\mathrm{2}\right)\mathrm{ln}\left(\frac{\mathrm{2x}+\mathrm{3}}{\mathrm{2x}−\mathrm{1}}\right)\:\sim\mathrm{4}.\frac{\mathrm{4x}+\mathrm{2}}{\mathrm{2x}−\mathrm{1}}\:\sim\mathrm{8}\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:\sim\mathrm{e}^{\mathrm{8}} \:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{e}^{\mathrm{8}} \\ $$

Answered by mathmax by abdo last updated on 10/Sep/20

2)let g(x) =(((3x+1)/(3x−1)))^(4x−2) ⇒g(x) =e^((4x−2)ln(((3x+1)/(3x−1)))) we have ln(((3x+1)/(3x−1))) =ln(((3x−1+2)/(3x−1))) =ln( 1+(2/(3x−1)))∼(2/(3x−1)) ⇒ (4x−2)ln(((3x+1)/(3x−1))) ∼2×((4x−2)/(3x−1)) ∼(8/3) ⇒lim_(x→∞) g(x) =e^(8/3)

$$\left.\mathrm{2}\right)\mathrm{let}\:\mathrm{g}\left(\mathrm{x}\right)\:=\left(\frac{\mathrm{3x}+\mathrm{1}}{\mathrm{3x}−\mathrm{1}}\right)^{\mathrm{4x}−\mathrm{2}} \:\Rightarrow\mathrm{g}\left(\mathrm{x}\right)\:=\mathrm{e}^{\left(\mathrm{4x}−\mathrm{2}\right)\mathrm{ln}\left(\frac{\mathrm{3x}+\mathrm{1}}{\mathrm{3x}−\mathrm{1}}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{ln}\left(\frac{\mathrm{3x}+\mathrm{1}}{\mathrm{3x}−\mathrm{1}}\right)\:=\mathrm{ln}\left(\frac{\mathrm{3x}−\mathrm{1}+\mathrm{2}}{\mathrm{3x}−\mathrm{1}}\right)\:=\mathrm{ln}\left(\:\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3x}−\mathrm{1}}\right)\sim\frac{\mathrm{2}}{\mathrm{3x}−\mathrm{1}}\:\Rightarrow \\ $$$$\left(\mathrm{4x}−\mathrm{2}\right)\mathrm{ln}\left(\frac{\mathrm{3x}+\mathrm{1}}{\mathrm{3x}−\mathrm{1}}\right)\:\sim\mathrm{2}×\frac{\mathrm{4x}−\mathrm{2}}{\mathrm{3x}−\mathrm{1}}\:\sim\frac{\mathrm{8}}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{g}\left(\mathrm{x}\right)\:=\mathrm{e}^{\frac{\mathrm{8}}{\mathrm{3}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com