Question Number 112902 by mohammad17 last updated on 10/Sep/20
$${find}\:{the}\:{angle}\:{between}\:\mathrm{3}{y}+\frac{{x}}{\:\sqrt{\mathrm{3}}}=\mathrm{1}\:,\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{y}−{x}=\mathrm{2} \\ $$$${help}\:{me}\:{sir} \\ $$
Answered by bemath last updated on 10/Sep/20
$$\mathrm{m}_{\mathrm{1}} =\:\frac{−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}}{\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}}\:;\:\mathrm{m}_{\mathrm{2}} =\:\frac{\mathrm{1}}{\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{say}\:\mathrm{the}\:\mathrm{angle}\:\mathrm{between}\:\mathrm{both}\:\mathrm{line} \\ $$$$\mathrm{is}\:\alpha\:\mathrm{then}\:\mathrm{tan}\:\alpha=\mid\frac{\mathrm{m}_{\mathrm{2}} −\mathrm{m}_{\mathrm{1}} }{\mathrm{1}+\mathrm{m}_{\mathrm{2}} .\mathrm{m}_{\mathrm{1}} }\mid \\ $$$$\mathrm{tan}\:\alpha=\mid\frac{\frac{\mathrm{6}+\mathrm{1}}{\:\mathrm{3}\sqrt{\mathrm{3}}}}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{9}}}\mid\:=\:\frac{\frac{\mathrm{21}}{\:\sqrt{\mathrm{3}}}}{\mathrm{7}}\:=\:\frac{\mathrm{3}}{\:\sqrt{\mathrm{3}}} \\ $$$$\alpha\:=\:\mathrm{tan}^{−\mathrm{1}} \left(\sqrt{\mathrm{3}}\:\right)\:=\:\mathrm{60}° \\ $$
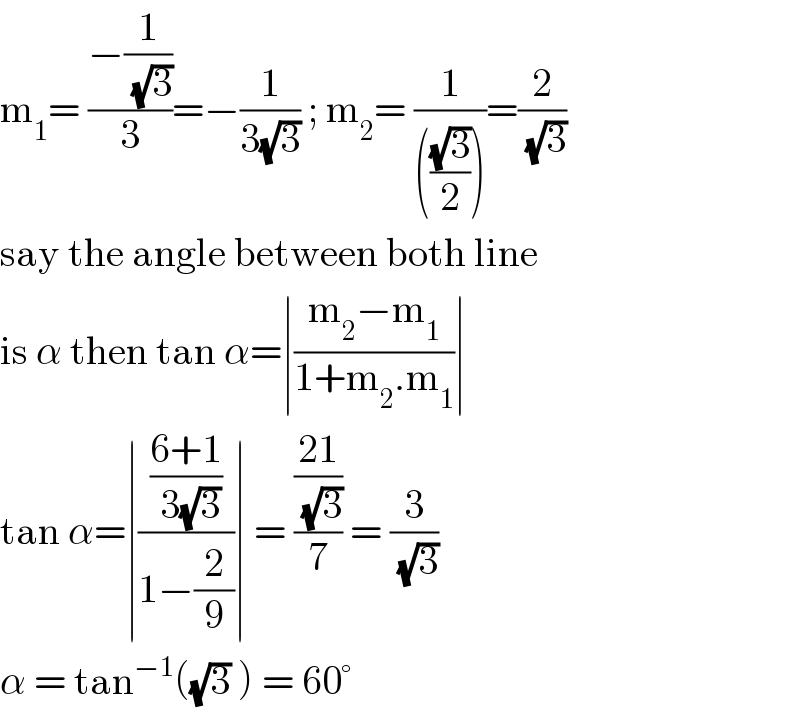
Commented by mohammad17 last updated on 10/Sep/20
$${thank}\:{you}\:{sir} \\ $$
Answered by mathmax by abdo last updated on 10/Sep/20
![3y+(x/(√3)) =1 ⇒3(√3)y +x =(√3) ⇒x+3(√3)y−(√3)=0 ⇒the director verctor is u^→ (−3(√3),1) ((√3)/2)y−x =2 ⇒(√3)y−2x =4 ⇒−2x+(√3)y−4=0 ⇒2x−(√3)y+4=0 ⇒ the director vector is v^→ ((√3),2) cos(u,v) =((u.v)/(∣u∣.∣v∣)) and sin(u,v) =((det(u,v))/(∣u∣.∣v∣)) ⇒tan(u,v) =((det(u,v))/(u.v)) =( determinant (((−3(√3) (√3))),((1 2)))/((−3(√3)).(√3)+1×2)) =((−7(√3))/(−7)) =(√3) we have tan(u,v) =(√3) ⇒(u,v) =(u,v) =(π/3)[π]](Q112950.png)
$$\mathrm{3y}+\frac{\mathrm{x}}{\sqrt{\mathrm{3}}}\:=\mathrm{1}\:\Rightarrow\mathrm{3}\sqrt{\mathrm{3}}\mathrm{y}\:+\mathrm{x}\:=\sqrt{\mathrm{3}}\:\Rightarrow\mathrm{x}+\mathrm{3}\sqrt{\mathrm{3}}\mathrm{y}−\sqrt{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{the}\:\mathrm{director}\:\mathrm{verctor}\:\mathrm{is}\:\overset{\rightarrow} {\mathrm{u}}\left(−\mathrm{3}\sqrt{\mathrm{3}},\mathrm{1}\right) \\ $$$$\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{y}−\mathrm{x}\:=\mathrm{2}\:\Rightarrow\sqrt{\mathrm{3}}\mathrm{y}−\mathrm{2x}\:=\mathrm{4}\:\Rightarrow−\mathrm{2x}+\sqrt{\mathrm{3}}\mathrm{y}−\mathrm{4}=\mathrm{0}\:\Rightarrow\mathrm{2x}−\sqrt{\mathrm{3}}\mathrm{y}+\mathrm{4}=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{the}\:\mathrm{director}\:\mathrm{vector}\:\mathrm{is}\:\overset{\rightarrow} {\mathrm{v}}\left(\sqrt{\mathrm{3}},\mathrm{2}\right) \\ $$$$\mathrm{cos}\left(\mathrm{u},\mathrm{v}\right)\:=\frac{\mathrm{u}.\mathrm{v}}{\mid\mathrm{u}\mid.\mid\mathrm{v}\mid}\:\mathrm{and}\:\mathrm{sin}\left(\mathrm{u},\mathrm{v}\right)\:=\frac{\mathrm{det}\left(\mathrm{u},\mathrm{v}\right)}{\mid\mathrm{u}\mid.\mid\mathrm{v}\mid}\:\Rightarrow\mathrm{tan}\left(\mathrm{u},\mathrm{v}\right)\:=\frac{\mathrm{det}\left(\mathrm{u},\mathrm{v}\right)}{\mathrm{u}.\mathrm{v}} \\ $$$$=\frac{\begin{vmatrix}{−\mathrm{3}\sqrt{\mathrm{3}}\:\:\:\:\:\:\:\:\sqrt{\mathrm{3}}}\\{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{vmatrix}}{\left(−\mathrm{3}\sqrt{\mathrm{3}}\right).\sqrt{\mathrm{3}}+\mathrm{1}×\mathrm{2}}\:=\frac{−\mathrm{7}\sqrt{\mathrm{3}}}{−\mathrm{7}}\:=\sqrt{\mathrm{3}} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{tan}\left(\mathrm{u},\mathrm{v}\right)\:=\sqrt{\mathrm{3}}\:\Rightarrow\left(\mathrm{u},\mathrm{v}\right)\:=\left(\mathrm{u},\mathrm{v}\right)\:=\frac{\pi}{\mathrm{3}}\left[\pi\right] \\ $$
Commented by mohammad17 last updated on 10/Sep/20
$${thank}\:{you}\:{sir} \\ $$
Commented by mathmax by abdo last updated on 11/Sep/20
$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$
Answered by Dwaipayan Shikari last updated on 10/Sep/20
$$\mathrm{3}{y}+\frac{{x}}{\:\sqrt{\mathrm{3}}}=\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{y}−{x}=\mathrm{2}\Rightarrow{y}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}{x}+\frac{\mathrm{4}}{\:\sqrt{\mathrm{3}}} \\ $$$${y}=−\frac{{x}}{\mathrm{3}\sqrt{\mathrm{3}}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${tan}\theta=\mid\frac{−\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{3}}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{9}}}\mid=\sqrt{\mathrm{3}} \\ $$$$\theta=\frac{\pi}{\mathrm{3}} \\ $$$$ \\ $$
Commented by mohammad17 last updated on 10/Sep/20
$${thank}\:{you}\:{sir} \\ $$