Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 112917 by abdullahquwatan last updated on 10/Sep/20

lim_(x→∞) [csc^2 ((2/x))−(1/4)x^2 ]

$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left[\mathrm{csc}^{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{x}}\right)−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{x}^{\mathrm{2}} \right] \\ $$

Commented by bobhans last updated on 10/Sep/20

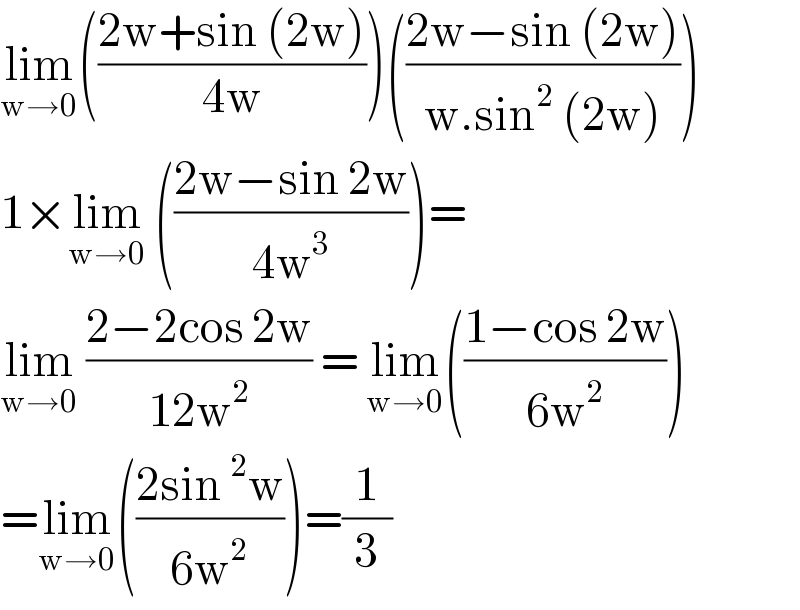
lim_(w→0) (((2w+sin (2w))/(4w)))(((2w−sin (2w))/(w.sin^2 (2w)))) 1×lim_(w→0) (((2w−sin 2w)/(4w^3 )))= lim_(w→0) ((2−2cos 2w)/(12w^2 )) = lim_(w→0) (((1−cos 2w)/(6w^2 ))) =lim_(w→0) (((2sin^2 w)/(6w^2 )))=(1/3)

$$\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2w}+\mathrm{sin}\:\left(\mathrm{2w}\right)}{\mathrm{4w}}\right)\left(\frac{\mathrm{2w}−\mathrm{sin}\:\left(\mathrm{2w}\right)}{\mathrm{w}.\mathrm{sin}^{\mathrm{2}} \:\left(\mathrm{2w}\right)}\right) \\ $$$$\mathrm{1}×\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{\mathrm{2w}−\mathrm{sin}\:\mathrm{2w}}{\mathrm{4w}^{\mathrm{3}} }\right)= \\ $$$$\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}−\mathrm{2cos}\:\mathrm{2w}}{\mathrm{12w}^{\mathrm{2}} }\:=\:\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2w}}{\mathrm{6w}^{\mathrm{2}} }\right) \\ $$$$=\underset{\mathrm{w}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{w}}{\mathrm{6w}^{\mathrm{2}} }\right)=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Commented by abdullahquwatan last updated on 10/Sep/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by abdullahquwatan last updated on 10/Sep/20

why 4w^3 ??

$$\mathrm{why}\:\mathrm{4w}^{\mathrm{3}} \:?? \\ $$

Answered by mathmax by abdo last updated on 10/Sep/20

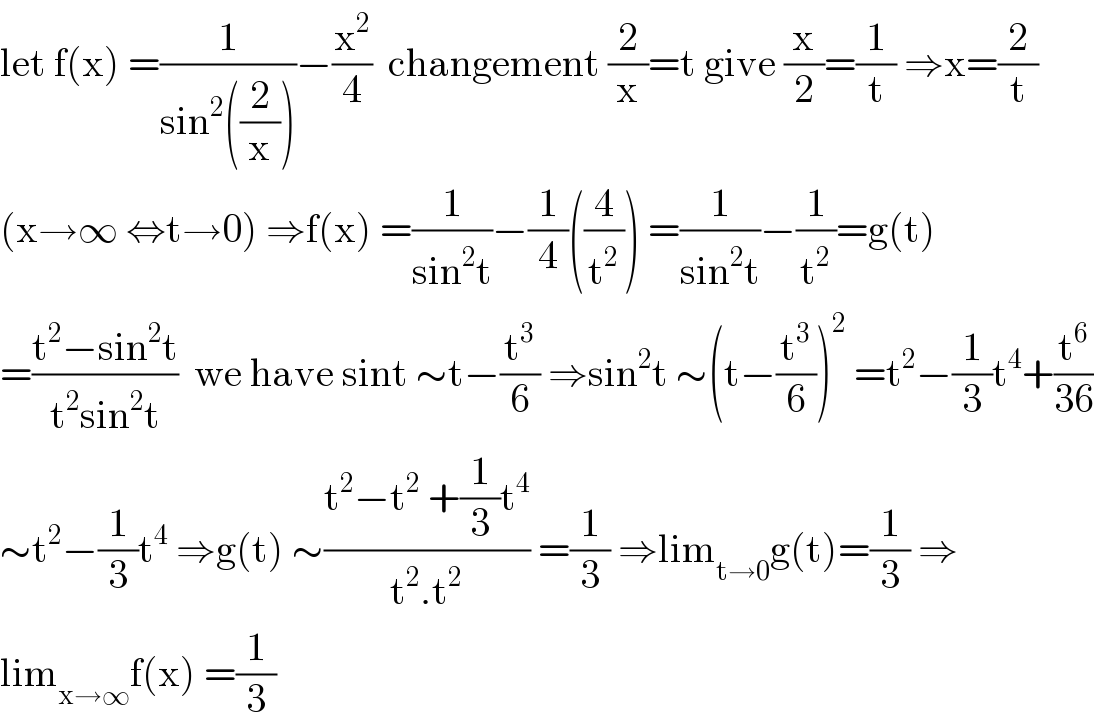
let f(x) =(1/(sin^2 ((2/x))))−(x^2 /4) changement (2/x)=t give (x/2)=(1/t) ⇒x=(2/t) (x→∞ ⇔t→0) ⇒f(x) =(1/(sin^2 t))−(1/4)((4/t^2 )) =(1/(sin^2 t))−(1/t^2 )=g(t) =((t^2 −sin^2 t)/(t^2 sin^2 t)) we have sint ∼t−(t^3 /6) ⇒sin^2 t ∼(t−(t^3 /6))^2 =t^2 −(1/3)t^4 +(t^6 /(36)) ∼t^2 −(1/3)t^4 ⇒g(t) ∼((t^2 −t^2 +(1/3)t^4 )/(t^2 .t^2 )) =(1/3) ⇒lim_(t→0) g(t)=(1/3) ⇒ lim_(x→∞) f(x) =(1/3)

$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \left(\frac{\mathrm{2}}{\mathrm{x}}\right)}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{4}}\:\:\mathrm{changement}\:\frac{\mathrm{2}}{\mathrm{x}}=\mathrm{t}\:\mathrm{give}\:\frac{\mathrm{x}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{t}}\:\Rightarrow\mathrm{x}=\frac{\mathrm{2}}{\mathrm{t}} \\ $$$$\left(\mathrm{x}\rightarrow\infty\:\Leftrightarrow\mathrm{t}\rightarrow\mathrm{0}\right)\:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}−\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{4}}{\mathrm{t}^{\mathrm{2}} }\right)\:=\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }=\mathrm{g}\left(\mathrm{t}\right) \\ $$$$=\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \mathrm{t}}{\mathrm{t}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \mathrm{t}}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{sint}\:\sim\mathrm{t}−\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{6}}\:\Rightarrow\mathrm{sin}^{\mathrm{2}} \mathrm{t}\:\sim\left(\mathrm{t}−\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{6}}\right)^{\mathrm{2}} \:=\mathrm{t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\mathrm{4}} +\frac{\mathrm{t}^{\mathrm{6}} }{\mathrm{36}} \\ $$$$\sim\mathrm{t}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\mathrm{4}} \:\Rightarrow\mathrm{g}\left(\mathrm{t}\right)\:\sim\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{t}^{\mathrm{4}} }{\mathrm{t}^{\mathrm{2}} .\mathrm{t}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{0}} \mathrm{g}\left(\mathrm{t}\right)=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\infty} \mathrm{f}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{3}} \\ $$

Commented by abdullahquwatan last updated on 10/Sep/20

thank you sir

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mathmax by abdo last updated on 11/Sep/20

you are welcome

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com