Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 112962 by mohammad17 last updated on 10/Sep/20

Commented by john santu last updated on 10/Sep/20

i think ∫_0 ^∞ t^8 e^(−4t) dt

$${i}\:{think}\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\:{t}^{\mathrm{8}} \:{e}^{−\mathrm{4}{t}} \:{dt} \\ $$

Commented by Dwaipayan Shikari last updated on 10/Sep/20

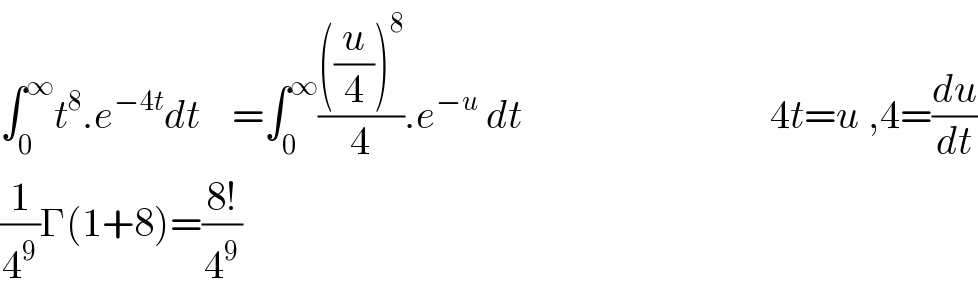
∫_0 ^∞ t^8 .e^(−4t) dt =∫_0 ^∞ ((((u/4))^8 )/4).e^(−u) dt 4t=u ,4=(du/dt) (1/4^9 )Γ(1+8)=((8!)/4^9 )

$$\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{8}} .{e}^{−\mathrm{4}{t}} {dt}\:\:\:\:=\int_{\mathrm{0}} ^{\infty} \frac{\left(\frac{{u}}{\mathrm{4}}\right)^{\mathrm{8}} }{\mathrm{4}}.{e}^{−{u}} \:{dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{4}{t}={u}\:,\mathrm{4}=\frac{{du}}{{dt}} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\Gamma\left(\mathrm{1}+\mathrm{8}\right)=\frac{\mathrm{8}!}{\mathrm{4}^{\mathrm{9}} } \\ $$

Commented by Aziztisffola last updated on 10/Sep/20

I think you mean ∫_0 ^( ∞) t^8 e^(−4t) dt In this case; here is the solution: let f(t)=t^8 ⇒ L{f(t)}=F(s)=((8!)/s^9 ) L {t^8 e^(−4t) }=L {f(t)e^(−4t) }=F(s+4) =((8!)/((s+4)^9 )) then ∫_0 ^( ∞) e^(−st) t^8 e^(−4t) dt=((8!)/((s+4)^9 )) let s=0 ⇒∫_0 ^( ∞) t^8 e^(−4t) dt= ((8!)/4^9 )

$$\mathrm{I}\:\mathrm{think}\:\mathrm{you}\:\mathrm{mean}\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{t}^{\mathrm{8}} \mathrm{e}^{−\mathrm{4t}} \mathrm{dt} \\ $$$$\:\mathrm{In}\:\mathrm{this}\:\mathrm{case};\:\mathrm{here}\:\mathrm{is}\:\mathrm{the}\:\mathrm{solution}: \\ $$$$\:\mathrm{let}\:\mathrm{f}\left(\mathrm{t}\right)=\mathrm{t}^{\mathrm{8}} \:\:\Rightarrow\:\mathscr{L}\left\{\mathrm{f}\left(\mathrm{t}\right)\right\}=\mathrm{F}\left(\mathrm{s}\right)=\frac{\mathrm{8}!}{\mathrm{s}^{\mathrm{9}} } \\ $$$$\:\mathscr{L}\:\left\{\mathrm{t}^{\mathrm{8}} \mathrm{e}^{−\mathrm{4t}} \right\}=\mathscr{L}\:\left\{\mathrm{f}\left(\mathrm{t}\right)\mathrm{e}^{−\mathrm{4t}} \right\}=\mathrm{F}\left(\mathrm{s}+\mathrm{4}\right) \\ $$$$\:=\frac{\mathrm{8}!}{\left(\mathrm{s}+\mathrm{4}\right)^{\mathrm{9}} } \\ $$$$\:\mathrm{then}\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{e}^{−\mathrm{st}} \mathrm{t}^{\mathrm{8}} \mathrm{e}^{−\mathrm{4t}} \mathrm{dt}=\frac{\mathrm{8}!}{\left(\mathrm{s}+\mathrm{4}\right)^{\mathrm{9}} } \\ $$$$\:\mathrm{let}\:\mathrm{s}=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\:\infty} \mathrm{t}^{\mathrm{8}} \mathrm{e}^{−\mathrm{4t}} \mathrm{dt}=\:\frac{\mathrm{8}!}{\mathrm{4}^{\mathrm{9}} }\: \\ $$$$\: \\ $$

Answered by Dwaipayan Shikari last updated on 10/Sep/20

x^8 ∫_0 ^∞ e^(−4t) dt (1/(−4))x^8 [e^(−4t) ]_0 ^∞ =(x^8 /4)

$${x}^{\mathrm{8}} \int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{4}{t}} {dt} \\ $$$$\frac{\mathrm{1}}{−\mathrm{4}}{x}^{\mathrm{8}} \left[{e}^{−\mathrm{4}{t}} \right]_{\mathrm{0}} ^{\infty} =\frac{{x}^{\mathrm{8}} }{\mathrm{4}} \\ $$

Commented by mohammad17 last updated on 10/Sep/20

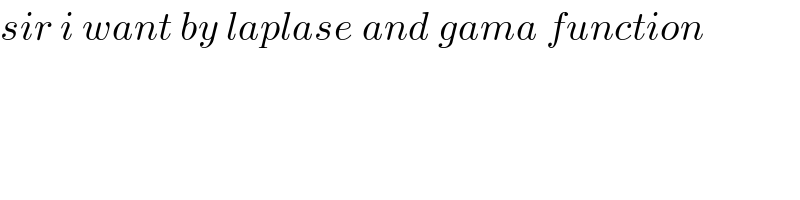
sir i want by laplase and gama function

$${sir}\:{i}\:{want}\:{by}\:{laplase}\:{and}\:{gama}\:{function} \\ $$

Answered by Aziztisffola last updated on 10/Sep/20

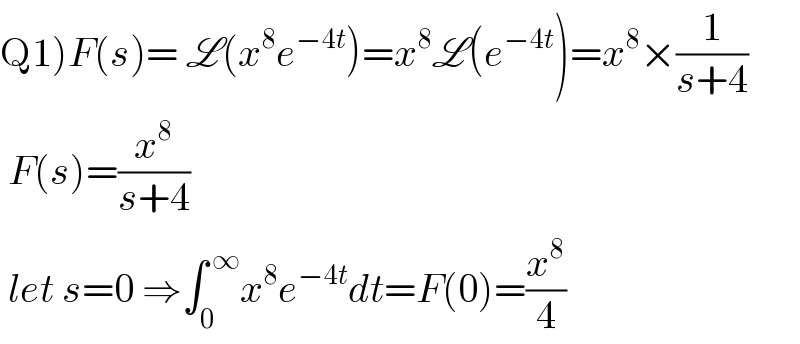
Q1)F(s)= L(x^8 e^(−4t) )=x^8 L(e^(−4t) )=x^8 ×(1/(s+4)) F(s)=(x^8 /(s+4)) let s=0 ⇒∫_0 ^( ∞) x^8 e^(−4t) dt=F(0)=(x^8 /4)

$$\left.\mathrm{Q1}\right){F}\left({s}\right)=\:\mathscr{L}\left({x}^{\mathrm{8}} {e}^{−\mathrm{4}{t}} \right)={x}^{\mathrm{8}} \mathscr{L}\left({e}^{−\mathrm{4}{t}} \right)={x}^{\mathrm{8}} ×\frac{\mathrm{1}}{{s}+\mathrm{4}} \\ $$$$\:{F}\left({s}\right)=\frac{{x}^{\mathrm{8}} }{{s}+\mathrm{4}} \\ $$$$\:{let}\:{s}=\mathrm{0}\:\Rightarrow\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{8}} {e}^{−\mathrm{4}{t}} {dt}={F}\left(\mathrm{0}\right)=\frac{{x}^{\mathrm{8}} }{\mathrm{4}} \\ $$

Answered by mathmax by abdo last updated on 11/Sep/20

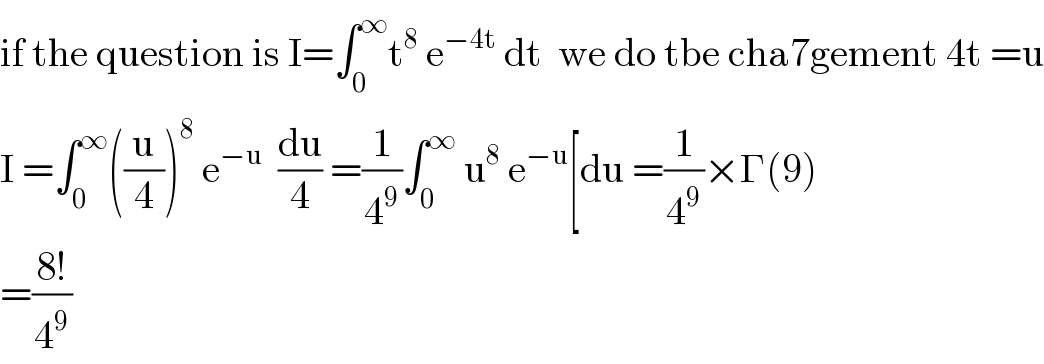
if the question is I=∫_0 ^∞ t^8 e^(−4t) dt we do tbe cha7gement 4t =u I =∫_0 ^∞ ((u/4))^8 e^(−u) (du/4) =(1/4^9 )∫_0 ^∞ u^8 e^(−u) [du =(1/4^9 )×Γ(9) =((8!)/4^9 )

$$\mathrm{if}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\mathrm{8}} \:\mathrm{e}^{−\mathrm{4t}} \:\mathrm{dt}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{cha7gement}\:\mathrm{4t}\:=\mathrm{u} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{u}}{\mathrm{4}}\right)^{\mathrm{8}} \:\mathrm{e}^{−\mathrm{u}} \:\:\frac{\mathrm{du}}{\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{u}^{\mathrm{8}} \:\mathrm{e}^{−\mathrm{u}} \left[\mathrm{du}\:=\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{9}} }×\Gamma\left(\mathrm{9}\right)\right. \\ $$$$=\frac{\mathrm{8}!}{\mathrm{4}^{\mathrm{9}} } \\ $$

Answered by mathmax by abdo last updated on 11/Sep/20

q_2 ) A =∫_0 ^∞ 3^(−4z^2 ) dz (i suppose z reel) A =∫_0 ^∞ e^(−4z^2 ln(3)) dz =∫_0 ^∞ e^(−(2(√(ln3))z)^2 ) dz we do the changement 2(√(ln3))z =u ⇒A =∫_0 ^∞ e^(−u^2 ) (du/(2(√(ln3)))) =(1/(2(√(ln3))))∫_0 ^∞ e^(−u^2 ) du =(1/(2(√(ln3))))×((√π)/2) =((√π)/(4(√(ln3))))

$$\left.\mathrm{q}_{\mathrm{2}} \right)\:\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{3}^{−\mathrm{4z}^{\mathrm{2}} } \mathrm{dz}\:\:\:\:\left(\mathrm{i}\:\mathrm{suppose}\:\mathrm{z}\:\mathrm{reel}\right) \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{4z}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{3}\right)} \:\mathrm{dz}\:\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\left(\mathrm{2}\sqrt{\mathrm{ln3}}\mathrm{z}\right)^{\mathrm{2}} } \mathrm{dz}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement} \\ $$$$\mathrm{2}\sqrt{\mathrm{ln3}}\mathrm{z}\:=\mathrm{u}\:\Rightarrow\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \:\frac{\mathrm{du}}{\mathrm{2}\sqrt{\mathrm{ln3}}}\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{ln3}}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \mathrm{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{ln3}}}×\frac{\sqrt{\pi}}{\mathrm{2}}\:=\frac{\sqrt{\pi}}{\mathrm{4}\sqrt{\mathrm{ln3}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com