
Question and Answers Forum
Question Number 113070 by ZiYangLee last updated on 11/Sep/20
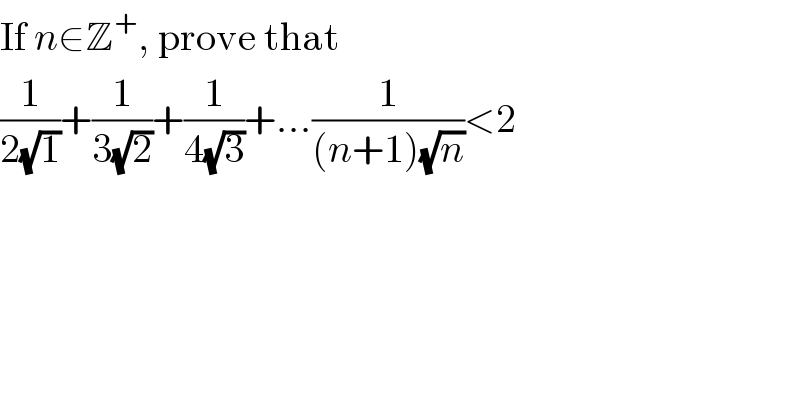
Answered by 1549442205PVT last updated on 11/Sep/20
![We have (1/((n+1)(√n)))=(√n).(1/((n+1)n)) =(√n)((1/n)−(1/(n+1)))=(√n)((1/( (√n)))+(1/( (√(n+1)))))((1/( (√n)))−(1/( (√(n+1))))) =(1+(1/( (√(n+1)))))((1/( (√n)))−(1/( (√(n+1))))) Since (1+(1/( (√(n+1)))))<2,so [(1/((n+1)(√n)))] <2((1/( (√n)))−(1/( (√(n+1))))).Hence,give n=1,2,... we get (1/(2(√1)))=(1/2)<2((1/1)−(1/( (√2)))),(1/(3(√2)))<2((1/( (√2)))−(1/( (√3)))), ...,(1/((n+1)(√n)))<2((1/( (√n)))−(1/( (√(n+1))))) Adding up n above inequalities we get LHS=(1/(2(√1)))+(1/(3(√2)))+(1/(4(√3)))+...(1/((n+1)(√n)))< 2[(1/( (√1)))−(1/( (√2)))+(1/( (√2)))−(1/( (√3)))+...+(1/( (√n)))−(1/( (√(n+1))))) =2(1−(1/( (√(n+1)))))<2 Therefore,we have (1/(2(√1)))+(1/(3(√2)))+(1/(4(√3)))+...(1/((n+1)(√n)))<2(q.e.d)](Q113108.png)
| ||
Question and Answers Forum | ||
Question Number 113070 by ZiYangLee last updated on 11/Sep/20 | ||
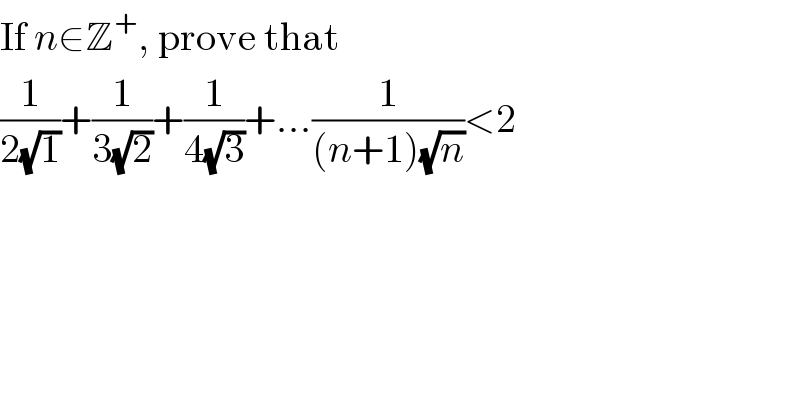 | ||
Answered by 1549442205PVT last updated on 11/Sep/20 | ||
![We have (1/((n+1)(√n)))=(√n).(1/((n+1)n)) =(√n)((1/n)−(1/(n+1)))=(√n)((1/( (√n)))+(1/( (√(n+1)))))((1/( (√n)))−(1/( (√(n+1))))) =(1+(1/( (√(n+1)))))((1/( (√n)))−(1/( (√(n+1))))) Since (1+(1/( (√(n+1)))))<2,so [(1/((n+1)(√n)))] <2((1/( (√n)))−(1/( (√(n+1))))).Hence,give n=1,2,... we get (1/(2(√1)))=(1/2)<2((1/1)−(1/( (√2)))),(1/(3(√2)))<2((1/( (√2)))−(1/( (√3)))), ...,(1/((n+1)(√n)))<2((1/( (√n)))−(1/( (√(n+1))))) Adding up n above inequalities we get LHS=(1/(2(√1)))+(1/(3(√2)))+(1/(4(√3)))+...(1/((n+1)(√n)))< 2[(1/( (√1)))−(1/( (√2)))+(1/( (√2)))−(1/( (√3)))+...+(1/( (√n)))−(1/( (√(n+1))))) =2(1−(1/( (√(n+1)))))<2 Therefore,we have (1/(2(√1)))+(1/(3(√2)))+(1/(4(√3)))+...(1/((n+1)(√n)))<2(q.e.d)](Q113108.png) | ||
| ||