
Question Number 11309 by FilupS last updated on 20/Mar/17
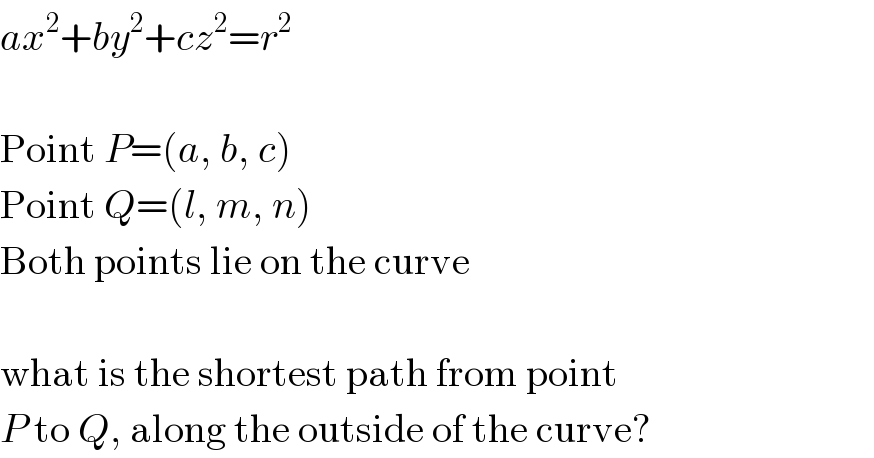
$${ax}^{\mathrm{2}} +{by}^{\mathrm{2}} +{cz}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\: \\ $$$$\mathrm{Point}\:{P}=\left({a},\:{b},\:{c}\right) \\ $$$$\mathrm{Point}\:{Q}=\left({l},\:{m},\:{n}\right) \\ $$$$\mathrm{Both}\:\mathrm{points}\:\mathrm{lie}\:\mathrm{on}\:\mathrm{the}\:\mathrm{curve} \\ $$$$\: \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{shortest}\:\mathrm{path}\:\mathrm{from}\:\mathrm{point} \\ $$$${P}\:\mathrm{to}\:{Q},\:\mathrm{along}\:\mathrm{the}\:\mathrm{outside}\:\mathrm{of}\:\mathrm{the}\:\mathrm{curve}? \\ $$
Commented by mrW1 last updated on 20/Mar/17
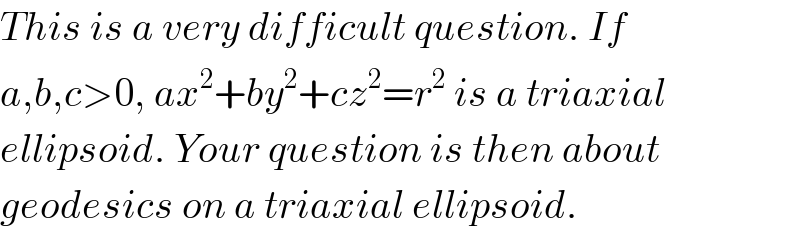
$${This}\:{is}\:{a}\:{very}\:{difficult}\:{question}.\:{If} \\ $$$${a},{b},{c}>\mathrm{0},\:{ax}^{\mathrm{2}} +{by}^{\mathrm{2}} +{cz}^{\mathrm{2}} ={r}^{\mathrm{2}} \:{is}\:{a}\:{triaxial} \\ $$$${ellipsoid}.\:{Your}\:{question}\:{is}\:{then}\:{about} \\ $$$${geodesics}\:{on}\:{a}\:{triaxial}\:{ellipsoid}. \\ $$
Commented by FilupS last updated on 21/Mar/17
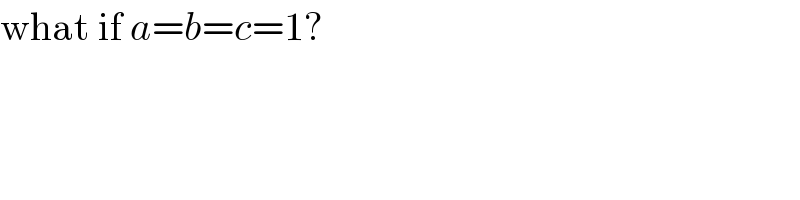
$$\mathrm{what}\:\mathrm{if}\:{a}={b}={c}=\mathrm{1}? \\ $$
Commented by mrW1 last updated on 21/Mar/17

$${Then}\:{it}\:{is}\:{a}\:{sphere}\:{with}\:{radius}\:{r}.\:{The}\:{shortest}\:{path} \\ $$$${on}\:{a}\:{sphere}\:{is}\:{the}\:{great}−{circle}\:{distance}. \\ $$$$ \\ $$$${Point}\:{P}\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} ,{z}_{\mathrm{1}} \right) \\ $$$${Point}\:{Q}\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} ,{z}_{\mathrm{2}} \right) \\ $$$${Vector}\:\boldsymbol{{p}}=\overset{\rightarrow} {{OP}},\:\boldsymbol{{q}}=\overset{\rightarrow} {{OQ}} \\ $$$${Angle}\:{between}\:\boldsymbol{{p}}\:{and}\:\boldsymbol{{q}}\:=\Delta\alpha \\ $$$$\mid\boldsymbol{{p}}\mid=\sqrt{{x}_{\mathrm{1}} ^{\mathrm{2}} +{y}_{\mathrm{1}} ^{\mathrm{2}} +{z}_{\mathrm{1}} ^{\mathrm{2}} }={r} \\ $$$$\mid\boldsymbol{{q}}\mid=\sqrt{{x}_{\mathrm{2}} ^{\mathrm{2}} +{y}_{\mathrm{2}} ^{\mathrm{2}} +{z}_{\mathrm{2}} ^{\mathrm{2}} }={r} \\ $$$$\mathrm{cos}\:\Delta\alpha=\frac{\boldsymbol{{p}}\centerdot\boldsymbol{{q}}}{\mid\boldsymbol{{p}}\mid×\mid\boldsymbol{{q}}\mid}=\frac{{x}_{\mathrm{1}} {x}_{\mathrm{2}} +{y}_{\mathrm{1}} {y}_{\mathrm{2}} +{z}_{\mathrm{1}} {z}_{\mathrm{2}} }{{r}^{\mathrm{2}} } \\ $$$$\Delta\alpha=\mathrm{cos}^{−\mathrm{1}} \left(\frac{{x}_{\mathrm{1}} {x}_{\mathrm{2}} +{y}_{\mathrm{1}} {y}_{\mathrm{2}} +{z}_{\mathrm{1}} {z}_{\mathrm{2}} }{{r}^{\mathrm{2}} }\right) \\ $$$$ \\ $$$${The}\:{shortest}\:{path}\:{from}\:{P}\:{to}\:{Q}\:{is} \\ $$$${d}=\Delta\alpha×{r} \\ $$
Commented by FilupS last updated on 21/Mar/17

$$\mathrm{fascinating}! \\ $$
