Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 113160 by mohammad17 last updated on 11/Sep/20

Commented by abdomsup last updated on 11/Sep/20

not correct Γ is defined on]0,∞[

$$\left.{not}\:{correct}\:\Gamma\:{is}\:{defined}\:{on}\right]\mathrm{0},\infty\left[\right. \\ $$

Commented by mohammad17 last updated on 11/Sep/20

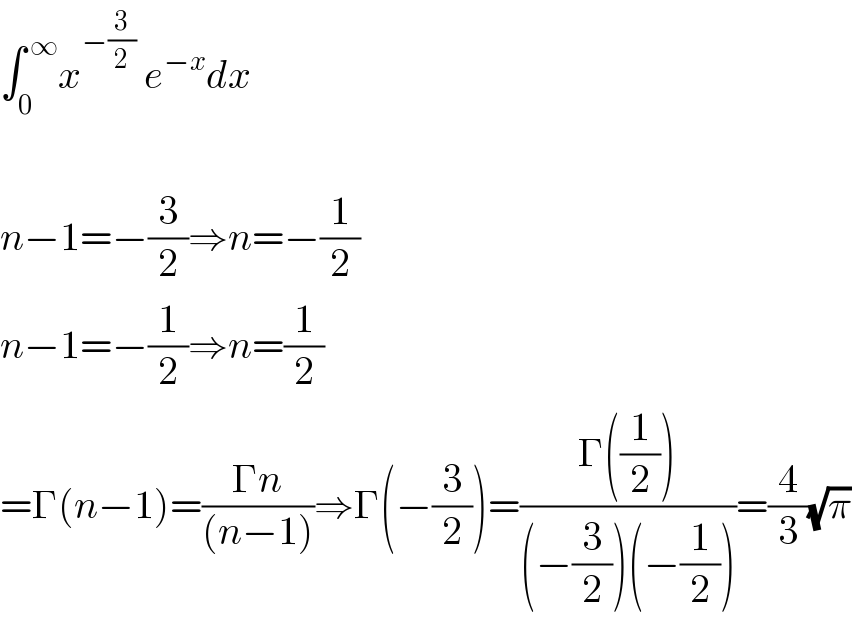
∫_0 ^( ∞) x^(−(3/2)) e^(−x) dx n−1=−(3/2)⇒n=−(1/2) n−1=−(1/2)⇒n=(1/2) =Γ(n−1)=((Γn)/((n−1)))⇒Γ(−(3/2))=((Γ((1/2)))/((−(3/2))(−(1/2))))=(4/3)(√π)

$$\int_{\mathrm{0}} ^{\:\infty} {x}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{e}^{−{x}} {dx} \\ $$$$ \\ $$$${n}−\mathrm{1}=−\frac{\mathrm{3}}{\mathrm{2}}\Rightarrow{n}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${n}−\mathrm{1}=−\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{n}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$=\Gamma\left({n}−\mathrm{1}\right)=\frac{\Gamma{n}}{\left({n}−\mathrm{1}\right)}\Rightarrow\Gamma\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)}=\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\pi} \\ $$

Commented by mohammad17 last updated on 11/Sep/20

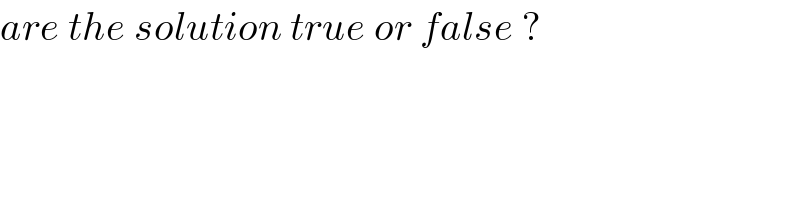
are the solution true or false ?

$${are}\:{the}\:{solution}\:{true}\:{or}\:{false}\:? \\ $$

Commented by 1549442205PVT last updated on 11/Sep/20

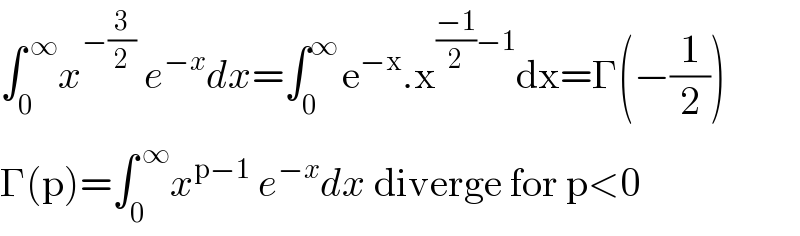
∫_0 ^( ∞) x^(−(3/2)) e^(−x) dx=∫_0 ^(∞ ) e^(−x) .x^(((−1)/2)−1) dx=Γ(−(1/2)) Γ(p)=∫_0 ^( ∞) x^(p−1) e^(−x) dx diverge for p<0

$$\int_{\mathrm{0}} ^{\:\infty} {x}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{e}^{−{x}} {dx}=\int_{\mathrm{0}} ^{\infty\:} \mathrm{e}^{−\mathrm{x}} .\mathrm{x}^{\frac{−\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \mathrm{dx}=\Gamma\left(−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Gamma\left(\mathrm{p}\right)=\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{p}−\mathrm{1}} \:{e}^{−{x}} {dx}\:\mathrm{diverge}\:\mathrm{for}\:\mathrm{p}<\mathrm{0} \\ $$

Answered by abdomsup last updated on 11/Sep/20

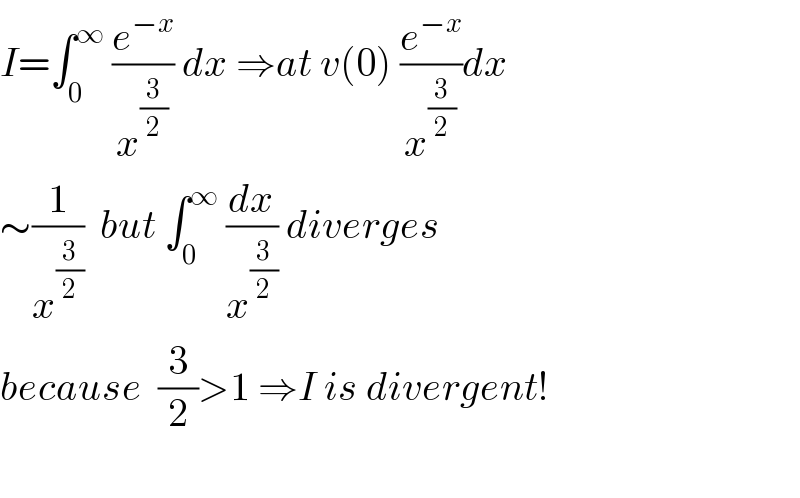
I=∫_0 ^∞ (e^(−x) /x^(3/2) ) dx ⇒at v(0) (e^(−x) /x^(3/2) )dx ∼(1/x^(3/2) ) but ∫_0 ^∞ (dx/x^(3/2) ) diverges because (3/2)>1 ⇒I is divergent!

$${I}=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}} }{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{dx}\:\Rightarrow{at}\:{v}\left(\mathrm{0}\right)\:\frac{{e}^{−{x}} }{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx} \\ $$$$\sim\frac{\mathrm{1}}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:{but}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{dx}}{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} }\:{diverges}\: \\ $$$${because}\:\:\frac{\mathrm{3}}{\mathrm{2}}>\mathrm{1}\:\Rightarrow{I}\:{is}\:{divergent}! \\ $$$$ \\ $$

Answered by MJS_new last updated on 11/Sep/20

∫x^q e^(−x) dx= [t=x^(q+1) → dx=(x^(−q) /(q+1))dt] =(1/(q+1))∫e^(−t^(1/(q+1)) ) dt= [incomplete Gamma−function] =(1/(q+1))(−(q+1)Γ (q+1∣t^(1/(q+1)) ))= =−Γ (q+1∣t^(1/(q+1)) )= =−Γ (q+1∣x) +C

$$\int{x}^{{q}} \mathrm{e}^{−{x}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}^{{q}+\mathrm{1}} \:\rightarrow\:{dx}=\frac{{x}^{−{q}} }{{q}+\mathrm{1}}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{{q}+\mathrm{1}}\int\mathrm{e}^{−{t}^{\frac{\mathrm{1}}{{q}+\mathrm{1}}} } {dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{incomplete}\:\mathrm{Gamma}−\mathrm{function}\right] \\ $$$$=\frac{\mathrm{1}}{{q}+\mathrm{1}}\left(−\left({q}+\mathrm{1}\right)\Gamma\:\left({q}+\mathrm{1}\mid{t}^{\frac{\mathrm{1}}{{q}+\mathrm{1}}} \right)\right)= \\ $$$$=−\Gamma\:\left({q}+\mathrm{1}\mid{t}^{\frac{\mathrm{1}}{{q}+\mathrm{1}}} \right)= \\ $$$$=−\Gamma\:\left({q}+\mathrm{1}\mid{x}\right)\:+{C} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com