
Question and Answers Forum
Question Number 113190 by Dwaipayan Shikari last updated on 11/Sep/20
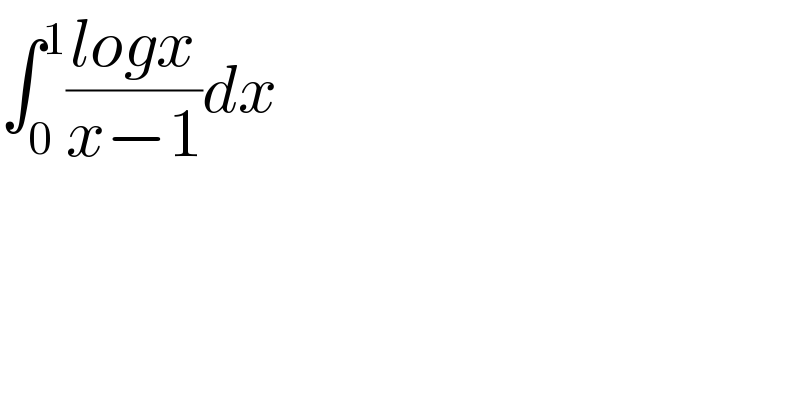
Commented by Dwaipayan Shikari last updated on 11/Sep/20
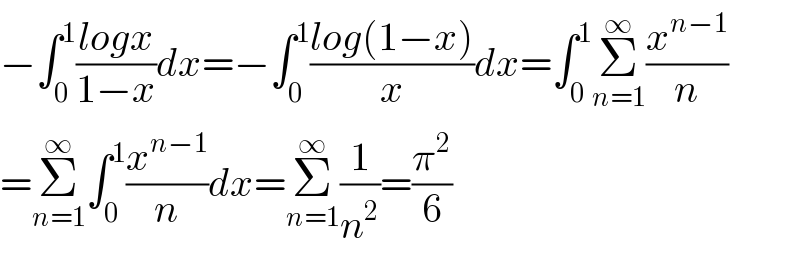
Commented by Dwaipayan Shikari last updated on 11/Sep/20

Commented by Tawa11 last updated on 06/Sep/21

Answered by mathdave last updated on 12/Sep/20
![solution let I=−∫_0 ^1 ((lnx)/(1−x))dx=−∫_0 ^1 Σ_(k=0) ^∞ x^k lnxdx (∂/∂a)∣_(a=1) I(a)=−Σ_(k=0) ^∞ (∂/∂a)∫_0 ^1 x^k .x^(a−1) dx=−Σ_(k=0) ^∞ (∂/∂a)∫_0 ^1 x^(k+a−1) dx I(a)=−Σ_(k=0) ^∞ (∂/∂a)[(1/(k+a))] I(1)=Σ_(k=0) ^∞ (1/((k+1)^2 ))=Σ_(k=1) ^∞ (1/k^2 )=(π^2 /6) ∵∫_0 ^1 ((lnx)/(x−1))dx=(π^2 /6)](Q113220.png)
