Question Number 113278 by mathdave last updated on 12/Sep/20
$${solve} \\ $$$$\int\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{2}−\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}}}{{x}\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }}{dx} \\ $$
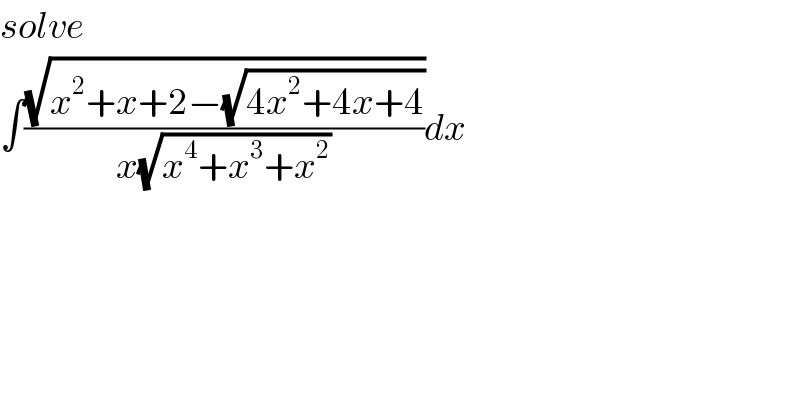
Answered by 1549442205PVT last updated on 13/Sep/20
![x^2 +x+2−(√(4x^2 +4x+4))= ((√(x^2 +x+1)))^2 −2(√(x^2 +x+1))+1 =((√(x^2 +x+1))−1)^2 ,x(√(x^4 +x^3 +x^2 ))=x^2 (√(x^2 +x+1)) Hence,F=∫((√(x^2 +x+2−(√(4x^2 +4x+4))))/(x(√(x^4 +x^3 +x^2 ))))dx =∫(((√(x^2 +x+1))−1)/(x^2 (√(x^2 +x+1))))dx=∫((1/x^2 )−(1/(x^2 (√(x^2 +x+1)))))dx We find J=∫(dx/(x^2 (√(x^2 +x+1))))=∫((√(x^2 +x+1))/(x^2 (x^2 +x+1)))dx =∫(√(x^2 +x+1))(((−x+1)/x^2 )+(x/(x^2 +x+1)))dx =∫(((√(x^2 +x+1))/x^2 )−((√(x^2 +x+1))/x)+(x/( (√(x^2 +x+1)))))dx ==∫[((√(x^2 +x+1))/x^2 )−((√(x^2 +x+1))/x)−(1/(2(√(x^2 +x+1))))+((1/2)×((2x+1)/( (√(x^2 +x+1)))))]dx (1/2)∫((2x+1)/( (√(x^2 +x+1))))dx=(1/2)∫(du/( (√u)))(u=x^2 +x+1) =(√(x^2 +x+1)) Since ∫(dx/( (√(x^2 +λ))))=ln∣x+(√(x^2 +λ))∣+C (1/2)∫(dx/( (√(x^2 +x+1))))=(1/2)∫((d(x+(1/2)))/( (√((x+(1/2))^2 +(3/4)))))=(1/2)ln∣x+(1/2)+(√(x^2 +x+1))∣ Therefore,we just need find =∫(((√(x^2 +x+1))/x^2 )−((√(x^2 +x+1))/x))]dx=A+B A=∫((√(x^2 +x+1))/x^2 )= −∫(√(x^2 +x+1))d((1/x)) = _(by part) ((−(√(x^2 +x+1)))/x)+∫(1/x)×((2x+1)/( 2(√(x^2 +x+1))))dx =((−(√(x^2 +x+1)))/x)+∫(dx/( (√(x^2 +x+1))))+∫(dx/(2x(√(x^2 +x+1)))) =((−(√(x^2 +x+1)))/x)+ln∣x+(1/2)+(√(x^2 +x+1))∣+(1/2)M(1) B=∫((√(x^2 +x+1))/x)dx= _(by parts) (√(x^2 +x+1))− −∫[x.((.((((2x+1)x)/(2(√(x^2 +x+1))))−(√(x^2 +x+1))))/x^2 )]dx =(√(x^2 +x+1))−∫((−x−2)/(2x(√(x^2 +x+1))))dx =(√(x^2 +x+1))+∫(dx/(2(√(x^2 +x+1))))+∫(dx/(x(√(x^2 +x+1)))) =(√(x^2 +x+1))+(1/2)ln∣x+(1/2)+(√(x^2 +x+1))∣+M (2) M=∫(dx/(x(√(x^2 +x+1))))=∫((2/(2x(√(x^2 +x+1))))×((2x+1−2(√(x^2 +x+1)))/(2x+1−2(√(x^2 +x+1)))))dx =∫(((2x+1−2(√(x^2 +x+1)))/(2(√(x^2 +x+1))))×(2/(x(2x+1)−2(√(x^2 +x+1)))))dx =∫(((2x+1)/(2(√(x^2 +x+1))))−1)((1/( (√(x^2 +x+1))−x−1))−(1/( (√(x^2 +x+1))−x+1)))dx =∫(((((2x+1)/(2(√(x^2 +x+1))))−1)/( (√(x^2 +x+1))−x−1))−((((2x+1)/(2(√(x^2 +x+1))))−1)/( (√(x^2 +x+1))−x+1)))dx =ln∣ (√(x^2 +x+1))−x−1∣−ln∣ (√(x^2 +x+1))−x+1∣ =ln∣(( (√(x^2 +x+1))−x−1)/( (√(x^2 +x+1))−x+1))∣(3) From (1)(2)(3)we get A+B=−((√(x^2 +x+1))/x)+ln∣x+(1/2)+(√(x^2 +x+1))∣ +(√(x^2 +x+1))+(1/2)ln∣x+(1/2)+(√(x^2 +x+1))∣ +(3/2)ln∣(((√(x^2 +x+1))−x−1)/( (√(x^2 +x+1))−x+1))∣(4) Therefore,J=(√(x^2 +x+1))−(1/2)ln∣x+(1/2)+(√(x^2 +x+1))∣ +A+B=2(√(x^2 +x+1))+ln∣x+(1/2)+(√(x^2 +x+1))∣+ +(3/2)ln∣(((√(x^2 +x+1))−x−1)/( (√(x^2 +x+1))−x+1))∣.From that F=−(1/x)+J=−(1/x)+A+B=2(√(x^2 +x+1))+ln∣x+(1/2)+(√(x^2 +x+1))∣+ +(3/2)ln∣(((√(x^2 +x+1))−x−1)/( (√(x^2 +x+1))−x+1))∣+C(C−constant) Thus,final result is F=∫((√(x^2 +x+2−(√(4x^2 +4x+4))))/(x(√(x^4 +x^3 +x^2 ))))dx =−(1/x)+2(√(x^2 +x+1))+ln∣x+(1/2)+(√(x^2 +x+1))∣ +(3/2)ln∣(((√(x^2 +x+1))−x−1)/( (√(x^2 +x+1))−x+1))∣+C](Q113340.png)
$$\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{2}−\sqrt{\mathrm{4x}^{\mathrm{2}} +\mathrm{4x}+\mathrm{4}}= \\ $$$$\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\mathrm{1} \\ $$$$=\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{1}\right)^{\mathrm{2}} ,\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{4}} +\mathrm{x}^{\mathrm{3}} +\mathrm{x}^{\mathrm{2}} }=\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{Hence},\mathrm{F}=\int\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{2}−\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}}}{{x}\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }}{dx} \\ $$$$=\int\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx}=\int\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\right)\mathrm{dx} \\ $$$$\mathrm{We}\:\mathrm{find}\:\mathrm{J}=\int\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}=\int\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}^{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}\mathrm{dx} \\ $$$$=\int\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\left(\frac{−\mathrm{x}+\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\frac{\mathrm{x}}{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)\mathrm{dx} \\ $$$$=\int\left(\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}^{\mathrm{2}} }−\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}}+\frac{\mathrm{x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\right)\mathrm{dx} \\ $$$$==\int\left[\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}^{\mathrm{2}} }−\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}+\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\right)\right]\mathrm{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2x}+\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{du}}{\:\sqrt{\mathrm{u}}}\left(\mathrm{u}=\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right) \\ $$$$=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}} \\ $$$$\mathrm{Since}\:\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\lambda}}=\mathrm{ln}\mid\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\lambda}\mid+\mathrm{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{d}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)}{\:\sqrt{\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid \\ $$$$\mathrm{Therefore},\mathrm{we}\:\mathrm{just}\:\mathrm{need}\:\mathrm{find} \\ $$$$\left.=\int\left(\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}^{\mathrm{2}} }−\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}}\right)\right]\mathrm{dx}=\mathrm{A}+\mathrm{B} \\ $$$$\mathrm{A}=\int\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}^{\mathrm{2}} }=\:−\int\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mathrm{d}\left(\frac{\mathrm{1}}{\mathrm{x}}\right)\:\:\: \\ $$$$\underset{\mathrm{by}\:\mathrm{part}} {=\:\:\:}\frac{−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}}+\int\frac{\mathrm{1}}{\mathrm{x}}×\frac{\mathrm{2x}+\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx} \\ $$$$=\frac{−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}}+\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}+\int\frac{\mathrm{dx}}{\mathrm{2x}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}} \\ $$$$=\frac{−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}}+\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{M}\left(\mathrm{1}\right) \\ $$$$\mathrm{B}=\int\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}}\mathrm{dx}\underset{\mathrm{by}\:\mathrm{parts}} {=\:\:\:\:\:}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}− \\ $$$$−\int\left[\mathrm{x}.\frac{.\left(\frac{\left(\mathrm{2x}+\mathrm{1}\right)\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\right)}{\mathrm{x}^{\mathrm{2}} }\right]\mathrm{dx} \\ $$$$=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\int\frac{−\mathrm{x}−\mathrm{2}}{\mathrm{2x}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\mathrm{dx} \\ $$$$=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\int\frac{\mathrm{dx}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}+\int\frac{\mathrm{dx}}{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}} \\ $$$$=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid+\mathrm{M}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{M}=\int\frac{\mathrm{dx}}{\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}=\int\left(\frac{\mathrm{2}}{\mathrm{2x}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}×\frac{\mathrm{2x}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{2x}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\right)\mathrm{dx} \\ $$$$=\int\left(\frac{\mathrm{2x}+\mathrm{1}−\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}×\frac{\mathrm{2}}{\mathrm{x}\left(\mathrm{2x}+\mathrm{1}\right)−\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}\right)\mathrm{dx} \\ $$$$=\int\left(\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}−\mathrm{1}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}+\mathrm{1}}\right)\mathrm{dx} \\ $$$$=\int\left(\frac{\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}−\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}−\mathrm{1}}−\frac{\frac{\mathrm{2x}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}−\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}+\mathrm{1}}\right)\mathrm{dx} \\ $$$$=\mathrm{ln}\mid\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}−\mathrm{1}\mid−\mathrm{ln}\mid\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}+\mathrm{1}\mid \\ $$$$=\mathrm{ln}\mid\frac{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}−\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}+\mathrm{1}}\mid\left(\mathrm{3}\right) \\ $$$$\mathrm{From}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\left(\mathrm{3}\right)\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{A}+\mathrm{B}=−\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}}{\mathrm{x}}+\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid \\ $$$$+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid \\ $$$$+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}−\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}+\mathrm{1}}\mid\left(\mathrm{4}\right) \\ $$$$\mathrm{Therefore},\mathrm{J}=\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid \\ $$$$+\mathrm{A}+\mathrm{B}=\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid+ \\ $$$$+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}−\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}+\mathrm{1}}\mid.\mathrm{From}\:\mathrm{that} \\ $$$$\mathrm{F}=−\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{J}=−\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{A}+\mathrm{B}=\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid+ \\ $$$$+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}−\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}+\mathrm{1}}\mid+\mathrm{C}\left(\mathrm{C}−\mathrm{constant}\right) \\ $$$$\mathrm{Thus},\mathrm{final}\:\mathrm{result}\:\mathrm{is} \\ $$$$\mathrm{F}=\int\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{2}−\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}}}{{x}\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }}{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{x}}+\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}+\mathrm{ln}\mid\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}\mid \\ $$$$+\frac{\mathrm{3}}{\mathrm{2}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}−\mathrm{1}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}}−\mathrm{x}+\mathrm{1}}\mid+\mathrm{C} \\ $$
Commented by mathdave last updated on 12/Sep/20
$${nice}\:{one} \\ $$
Commented by 1549442205PVT last updated on 13/Sep/20
$$\mathrm{I}\:\mathrm{like}\:\mathrm{smart}\:\mathrm{Sir}'\mathrm{s}\:\mathrm{solution}\: \\ $$
Commented by Tawa11 last updated on 06/Sep/21
$$\mathrm{grest}\:\mathrm{sir} \\ $$
Answered by MJS_new last updated on 12/Sep/20
![∫((√(x^2 +x+1−2(√(x^2 +x+1))+1))/(x^2 (√(x^2 +x+1))))dx= =∫(dx/x^2 )−∫(dx/(x^2 (√(x^2 +x+1)))) (1) ∫(dx/x^2 )=−(1/x) (2) −∫(dx/(x^2 (√(x^2 +x+1))))= [t=((√3)/2)(2x+1+2(√(x^2 +x+1)) → dx=((√(3(x^2 +x+1)))/(2x+1+2(√(x^2 +x+1))))] =−16∫(t/( ((√3)t^2 −2t−(√3))^2 ))dt= =(√3)∫((1/(2((√3)t−3)))−(1/(2((√3)t+1)))−(3/(((√3)t−3)^2 ))+(1/(((√3)t+2)^2 )))dt= =((2(t+(√3)))/( (√3)t^2 −2t−(√3)))−(1/2)ln (((√3)t+1)/( (√3)t−3))= =((√(x^2 +x+1))/x)+(1/2)ln x −(1/2)ln (x+2+2(√(x^2 +x+1))) +C ⇒ ∫((√(x^2 +x+2−(√(4x^2 +4x+4))))/(x(√(x^4 +x^3 +x^2 ))))dx= =((−1+(√(x^2 +x+1)))/x)+(1/2)ln x −(1/2)ln (x+2+2(√(x^2 +x+1))) +C](Q113366.png)
$$\int\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}−\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}+\mathrm{1}}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{dx}= \\ $$$$=\int\frac{{dx}}{{x}^{\mathrm{2}} }−\int\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}} \\ $$$$\left(\mathrm{1}\right)\:\:\int\frac{{dx}}{{x}^{\mathrm{2}} }=−\frac{\mathrm{1}}{{x}} \\ $$$$\left(\mathrm{2}\right)\:\:−\int\frac{{dx}}{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{3}\left({x}^{\mathrm{2}} +{x}+\mathrm{1}\right)}}{\mathrm{2}{x}+\mathrm{1}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}\right]\right. \\ $$$$=−\mathrm{16}\int\frac{{t}}{\:\left(\sqrt{\mathrm{3}}{t}^{\mathrm{2}} −\mathrm{2}{t}−\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }{dt}= \\ $$$$=\sqrt{\mathrm{3}}\int\left(\frac{\mathrm{1}}{\mathrm{2}\left(\sqrt{\mathrm{3}}{t}−\mathrm{3}\right)}−\frac{\mathrm{1}}{\mathrm{2}\left(\sqrt{\mathrm{3}}{t}+\mathrm{1}\right)}−\frac{\mathrm{3}}{\left(\sqrt{\mathrm{3}}{t}−\mathrm{3}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\sqrt{\mathrm{3}}{t}+\mathrm{2}\right)^{\mathrm{2}} }\right){dt}= \\ $$$$=\frac{\mathrm{2}\left({t}+\sqrt{\mathrm{3}}\right)}{\:\sqrt{\mathrm{3}}{t}^{\mathrm{2}} −\mathrm{2}{t}−\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\sqrt{\mathrm{3}}{t}+\mathrm{1}}{\:\sqrt{\mathrm{3}}{t}−\mathrm{3}}= \\ $$$$=\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{x}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\mathrm{2}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)\:+{C} \\ $$$$ \\ $$$$\Rightarrow \\ $$$$ \\ $$$$\int\frac{\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{2}−\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{4}}}}{{x}\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{3}} +{x}^{\mathrm{2}} }}{dx}= \\ $$$$=\frac{−\mathrm{1}+\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}}{{x}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:{x}\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({x}+\mathrm{2}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} +{x}+\mathrm{1}}\right)\:+{C} \\ $$
Commented by Tawa11 last updated on 06/Sep/21
$$\mathrm{great}\:\mathrm{sir} \\ $$