y′′−2ay′+(1+a^2 )y=te^(at) +sint


Question and Answers Forum

All Questions Topic List
Differentiation Questions
Previous in All Question Next in All Question
Previous in Differentiation Next in Differentiation
Question Number 113444 by Ar Brandon last updated on 13/Sep/20

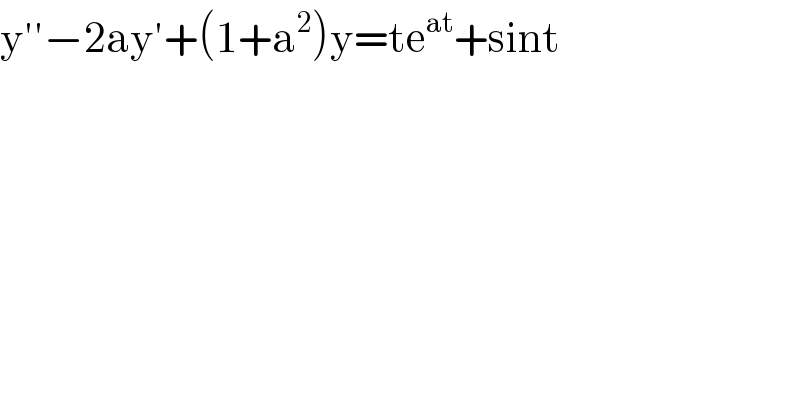
$y^{″} - {2 ay}^{'} + (1 + a^{2}) y = {te}^{at} + sint$
	Answered by Ar Brandon last updated on 13/Sep/20
	$y′′−2ay′+(1+a^2 )y=te^(at) +sint (h)→r^2 −2ar+1+a^2 =0⇒r=((2a±(√(4a^2 −4(1+a^2 ))))/2)=a±i y_h =e^(at) (Acost+Bsint) By varying parameters let; y_p =A(t)e^(at) cost+B(t)e^(at) sint ⇒y_p =au_1 +bu_2 { ((a′u_1 +b′u_2 =0),(...(1))),((a′u_1 ′+b′u_2 ′=te^(at) +sint),(...(2))) :} Finding a′ and b′ using Crammer′s method; W(u_1 ,u_2 )= determinant ((u_1 ,u_2 ),((u_1 ′),(u_2 ′)))= determinant (((e^(at) cost),(e^(at) sint)),((ae^(at) cost−e^(at) sint),(e^(at) cost+ae^(at) sint))) =e^(2at) [(cos^2 t+asintcost)−(asintcost−sin^2 t)]=e^(2at) w_1 = determinant ((0,(e^(at) sint)),((te^(at) +sint),(e^(at) cost+ae^(at) sint)))=−(te^(2at) sint+e^(at) sin^2 t) w_2 = determinant (((e^(at) cost),0),((ae^(at) cost−e^(at) sint),(te^(at) +sint)))=te^(2at) cost+e^(at) sintcost a′=(w_1 /W)⇒a=∫(w_1 /W)dt , b′=(w_2 /W)⇒b=∫(w_2 /W)dt ⇒A(t)=−∫((te^(2at) sint+e^(at) sin^2 t)/e^(2at) )dt, B(t)=∫((te^(2at) cost+e^(at) sintcost)/e^(2at) )dt A(t)=−∫(tsint+e^(−at) sin^2 t)dt ∫tsintdt=−tcost+∫costdt=sint−tcost ∫e^(−at) sin^2 tdt=−((sin^2 t)/a)∙e^(−at) +(2/a)∫sintcost∙e^(−at) dt =−((sin^2 t)/a)∙e^(−at) +(1/a)∫sin(2t)e^(−at) dt =−((sin^2 t)/a)∙e^(−at) +(1/a){−((sin(2t))/a)e^(−at) +(2/a)∫cos(2t)e^(−at) dt} =−((sin^2 t)/a)∙e^(−at) −((sin(2t))/a^2 )e^(−at) +(2/a^2 )[−((cos(2t))/a)e^(−at) −(2/a)∫sin(2t)e^(−at) dt] =−((sin^2 t)/a)∙e^(−at) −((sin(2t))/a^2 )e^(−at) −((2cos(2t))/a^3 )e^(−at) −(4/a^3 )∫sin(2t)e^(−at) dt =−((sin^2 t)/a)∙e^(−at) +(a^3 /(a^2 +4))[−((sin(2t))/a^2 )e^(−at) −((2cos(2t))/a^3 )e^(−at) ]+C ⇒A(t)=tcost−sint+((sin^2 t)/a)∙e^(−at) +(a^3 /(a^2 +4))[((sin(2t))/a^2 )e^(−at) +((2cos(2t))/a^3 )e^(−at) ]+C B(t)=∫((te^(2at) cost+e^(at) sintcost)/e^(2at) )dt=∫(tcost+e^(−at) sintcost)dt ∫tcostdt=tsint−∫sintdt=tsint+cost ∫e^(−at) sintcostdt=(1/2)∫e^(−at) sin(2t)dt =(1/2)∙(a^4 /(a^2 +4))[−((sin(2t))/a^2 )e^(−at) −((2cos(2t))/a^3 )e^(−at) ]+K ⇒B(t)=tsint+cost+(1/2)∙(a^4 /(a^2 +4))[−((sin(2t))/a^2 )e^(−at) −((2cos(2t))/a^3 )e^(−at) ]+K Or y_p =A(t)e^(at) cost+B(t)e^(at) sint et y_G =y_h +y_p y_G =e^(at) (Acost+Bsint)+e^(at) tcos^2 t−e^(at) sintcost+((sin^2 tcost)/a)+((a^3 cost)/(a^2 +4))[((sin(2t))/a^2 )+((2cos(2t))/a^3 )]+Ce^(at) cost e^(at) tsintcost+e^(at) cos^2 t+(1/2)∙((a^4 cost)/(a^2 +4))[−((sin(2t))/a^2 )−((2cos(2t))/a^3 )]+Ke^(at) cost$
	$y^{″} - {2 ay}^{'} + (1 + a^{2}) y = {te}^{at} + sint$ $(h) \to r^{2} - 2 ar + 1 + a^{2} = 0 \Rightarrow r = \frac{2 a \pm \sqrt{{4 a}^{2} - 4 (1 + a^{2})}}{2} = a \pm i$ $y_{h} = e^{at} (Acost + Bsint)$ $By varying parameters let; y_{p} = A (t) e^{at} cost + B (t) e^{at} sint$ $\Rightarrow y_{p} = {au}_{1} + {bu}_{2}$ ${\begin{cases} a^{'} u_{1} + b^{'} u_{2} = 0 & . . . (1) \\ a^{'} u_{1}^{'} + b^{'} u_{2}^{'} = {te}^{at} + sint & . . . (2) \end{cases}$ $Finding a^{'} and b^{'} using {Crammer}^{'} s method;$ $W (u_{1}, u_{2}) = \| \begin{matrix} u_{1} & u_{2} \\ u_{1}^{'} & u_{2}^{'} \end{matrix} \| = \| \begin{matrix} e^{at} cost & e^{at} sint \\ {ae}^{at} cost - e^{at} sint & e^{at} cost + {ae}^{at} sint \end{matrix} \|$ $= e^{2 at} [(\cos^{2} t + asintcost) - (asintcost - \sin^{2} t)] = e^{2 at}$ $w_{1} = \| \begin{matrix} 0 & e^{at} sint \\ {te}^{at} + sint & e^{at} cost + {ae}^{at} sint \end{matrix} \| = - ({te}^{2 at} sint + e^{at} \sin^{2} t)$ $w_{2} = \| \begin{matrix} e^{at} cost & 0 \\ {ae}^{at} cost - e^{at} sint & {te}^{at} + sint \end{matrix} \| = {te}^{2 at} cost + e^{at} sintcost$ $a^{'} = \frac{w_{1}}{W} \Rightarrow a = \int \frac{w_{1}}{W} dt, b^{'} = \frac{w_{2}}{W} \Rightarrow b = \int \frac{w_{2}}{W} dt$ $\Rightarrow A (t) = - \int \frac{{te}^{2 at} sint + e^{at} \sin^{2} t}{e^{2 at}} dt, B (t) = \int \frac{{te}^{2 at} cost + e^{at} sintcost}{e^{2 at}} dt$ $A (t) = - \int (tsint + e^{- at} \sin^{2} t) dt$ $\int tsintdt = - tcost + \int costdt = sint - tcost$ $\int e^{- at} \sin^{2} tdt = - \frac{\sin^{2} t}{a} \cdot e^{- at} + \frac{2}{a} \int sintcost \cdot e^{- at} dt$ $= - \frac{\sin^{2} t}{a} \cdot e^{- at} + \frac{1}{a} \int \sin (2 t) e^{- at} dt$ $= - \frac{\sin^{2} t}{a} \cdot e^{- at} + \frac{1}{a} {- \frac{\sin (2 t)}{a} e^{- at} + \frac{2}{a} \int \cos (2 t) e^{- at} dt}$ $= - \frac{\sin^{2} t}{a} \cdot e^{- at} - \frac{\sin (2 t)}{a^{2}} e^{- at} + \frac{2}{a^{2}} [- \frac{\cos (2 t)}{a} e^{- at} - \frac{2}{a} \int \sin (2 t) e^{- at} dt]$ $= - \frac{\sin^{2} t}{a} \cdot e^{- at} - \frac{\sin (2 t)}{a^{2}} e^{- at} - \frac{2 \cos (2 t)}{a^{3}} e^{- at} - \frac{4}{a^{3}} \int \sin (2 t) e^{- at} dt$ $= - \frac{\sin^{2} t}{a} \cdot e^{- at} + \frac{a^{3}}{a^{2} + 4} [- \frac{\sin (2 t)}{a^{2}} e^{- at} - \frac{2 \cos (2 t)}{a^{3}} e^{- at}] + C$ $\Rightarrow A (t) = tcost - sint + \frac{\sin^{2} t}{a} \cdot e^{- at} + \frac{a^{3}}{a^{2} + 4} [\frac{\sin (2 t)}{a^{2}} e^{- at} + \frac{2 \cos (2 t)}{a^{3}} e^{- at}] + C$ $B (t) = \int \frac{{te}^{2 at} cost + e^{at} sintcost}{e^{2 at}} dt = \int (tcost + e^{- at} sintcost) dt$ $\int tcostdt = tsint - \int sintdt = tsint + cost$ $\int e^{- at} sintcostdt = \frac{1}{2} \int e^{- at} \sin (2 t) dt$ $= \frac{1}{2} \cdot \frac{a^{4}}{a^{2} + 4} [- \frac{\sin (2 t)}{a^{2}} e^{- at} - \frac{2 \cos (2 t)}{a^{3}} e^{- at}] + K$ $\Rightarrow B (t) = tsint + cost + \frac{1}{2} \cdot \frac{a^{4}}{a^{2} + 4} [- \frac{\sin (2 t)}{a^{2}} e^{- at} - \frac{2 \cos (2 t)}{a^{3}} e^{- at}] + K$ $Or y_{p} = A (t) e^{at} cost + B (t) e^{at} sint et y_{G} = y_{h} + y_{p}$ $y_{G} = e^{at} (Acost + Bsint) + e^{at} {tcos}^{2} t - e^{at} sintcost + \frac{\sin^{2} tcost}{a} + \frac{a^{3} cost}{a^{2} + 4} [\frac{\sin (2 t)}{a^{2}} + \frac{2 \cos (2 t)}{a^{3}}] + {Ce}^{at} cost$ $e^{at} tsintcost + e^{at} \cos^{2} t + \frac{1}{2} \cdot \frac{a^{4} cost}{a^{2} + 4} [- \frac{\sin (2 t)}{a^{2}} - \frac{2 \cos (2 t)}{a^{3}}] + {Ke}^{at} cost$
	Commented by bemath last updated on 13/Sep/20

	$a m a z i n g$
	Commented by bobhans last updated on 13/Sep/20

	$super great . . . .$
	Commented by Ar Brandon last updated on 13/Sep/20
	��
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum