
Question and Answers Forum
Question Number 113628 by mathmax by abdo last updated on 14/Sep/20
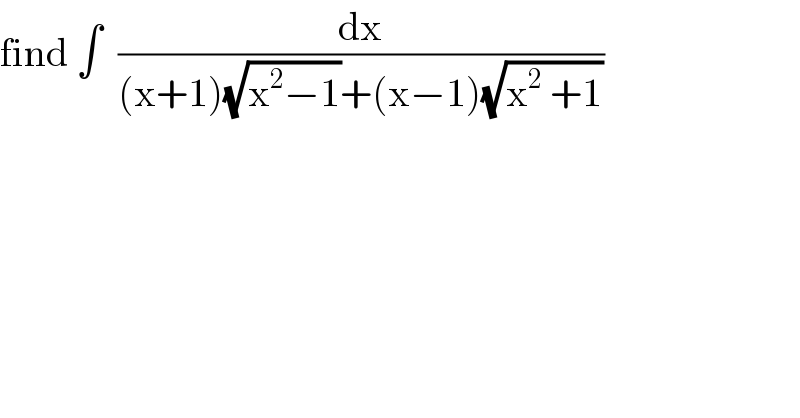
Answered by MJS_new last updated on 16/Sep/20
![∫(dx/((x+1)(√(x^2 −1))+(x−1)(√(x^2 +1))))= =∫(((x+1)(√(x^2 −1))−(x−1)(√(x^2 +1)))/(2(x−1)(2x^2 +x+1)))dx= =(1/4)∫((√(x^2 −1))/(x−1))dx−(1/2)∫((√(x^2 +1))/(2x^2 +x+1))dx−(1/4)∫(((2x+1)(√(x^2 −1)))/(2x^2 +x+1))dx (1/4)∫((√(x^2 −1))/(x−1))dx= ( ) [t=x+(√(x^2 −1)) → dx=((√(x^2 −1))/(x+(√(x^2 −1))))dt] =(1/8)∫(((t+1)^2 )/t^2 )dt=((t^2 −1)/(8t))+(1/4)ln t = =(1/4)(√(x^2 −1))+(1/4)ln (x+(√(x^2 −1))) −(1/2)∫((√(x^2 +1))/(2x^2 +x+1))dx= [t=x+(√(x^2 +1)) → dx=((√(x^2 +1))/(x+(√(x^2 +1))))] =−(1/4)∫(((t^2 +1)^2 )/(t(t^4 +t^3 −t+1)))dt now we must decompose t^4 +t^3 −t+1=(t^2 +αt+β)(t^2 +γt+δ) α=((1+(√(5+4(√2))))/2) β=((1+(√2))/2)+(((√(5+4(√2)))+(√(−35+28(√2))))/8) γ=((1−(√(5+4(√2))))/2) δ=((1+(√2))/2)−(((√(5+4(√2)))+(√(−35+28(√2))))/8) I′m too tired now −(1/4)∫(((2x+1)(√(x^2 −1)))/(2x^2 +x+1))dx= [t=x+(√(x^2 −1)) → dx=((√(x^2 −1))/(x+(√(x^2 −1))))] =−(1/8)∫(((t^2 −1)^2 (t^2 +t+1))/(t^2 (t^4 +t^3 +4t^2 +t+1)))dt again to decompose t^4 +t^3 +4t^2 +t+1=(t^2 +at+b)(t^2 +ct+d) a=((1+(√(−11+8(√2))))/2) b=((1+2(√2))/2)+(((√(−11+8(√2)))+(√(77+56(√2))))/8) c=((1−(√(−11+8(√2))))/2) d=((1+2(√2))/2)−(((√(−11+8(√2)))+(√(77+56(√2))))/8) please continue if you need it, I go to bed...](Q113880.png)
Commented by Dwaipayan Shikari last updated on 16/Sep/20
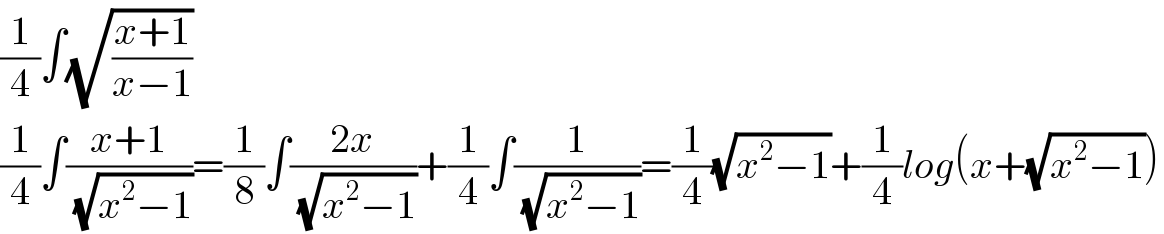
Commented by Tawa11 last updated on 06/Sep/21

| ||
Question and Answers Forum | ||
Question Number 113628 by mathmax by abdo last updated on 14/Sep/20 | ||
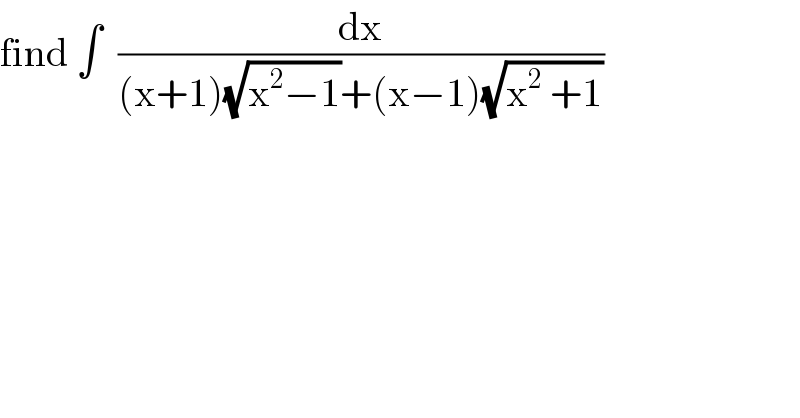 | ||
Answered by MJS_new last updated on 16/Sep/20 | ||
![∫(dx/((x+1)(√(x^2 −1))+(x−1)(√(x^2 +1))))= =∫(((x+1)(√(x^2 −1))−(x−1)(√(x^2 +1)))/(2(x−1)(2x^2 +x+1)))dx= =(1/4)∫((√(x^2 −1))/(x−1))dx−(1/2)∫((√(x^2 +1))/(2x^2 +x+1))dx−(1/4)∫(((2x+1)(√(x^2 −1)))/(2x^2 +x+1))dx (1/4)∫((√(x^2 −1))/(x−1))dx= ( ) [t=x+(√(x^2 −1)) → dx=((√(x^2 −1))/(x+(√(x^2 −1))))dt] =(1/8)∫(((t+1)^2 )/t^2 )dt=((t^2 −1)/(8t))+(1/4)ln t = =(1/4)(√(x^2 −1))+(1/4)ln (x+(√(x^2 −1))) −(1/2)∫((√(x^2 +1))/(2x^2 +x+1))dx= [t=x+(√(x^2 +1)) → dx=((√(x^2 +1))/(x+(√(x^2 +1))))] =−(1/4)∫(((t^2 +1)^2 )/(t(t^4 +t^3 −t+1)))dt now we must decompose t^4 +t^3 −t+1=(t^2 +αt+β)(t^2 +γt+δ) α=((1+(√(5+4(√2))))/2) β=((1+(√2))/2)+(((√(5+4(√2)))+(√(−35+28(√2))))/8) γ=((1−(√(5+4(√2))))/2) δ=((1+(√2))/2)−(((√(5+4(√2)))+(√(−35+28(√2))))/8) I′m too tired now −(1/4)∫(((2x+1)(√(x^2 −1)))/(2x^2 +x+1))dx= [t=x+(√(x^2 −1)) → dx=((√(x^2 −1))/(x+(√(x^2 −1))))] =−(1/8)∫(((t^2 −1)^2 (t^2 +t+1))/(t^2 (t^4 +t^3 +4t^2 +t+1)))dt again to decompose t^4 +t^3 +4t^2 +t+1=(t^2 +at+b)(t^2 +ct+d) a=((1+(√(−11+8(√2))))/2) b=((1+2(√2))/2)+(((√(−11+8(√2)))+(√(77+56(√2))))/8) c=((1−(√(−11+8(√2))))/2) d=((1+2(√2))/2)−(((√(−11+8(√2)))+(√(77+56(√2))))/8) please continue if you need it, I go to bed...](Q113880.png) | ||
| ||
Commented by Dwaipayan Shikari last updated on 16/Sep/20 | ||
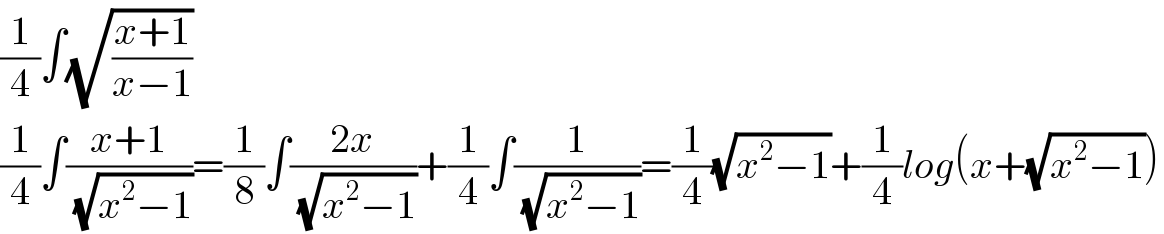 | ||
Commented by Tawa11 last updated on 06/Sep/21 | ||
 | ||