
Question and Answers Forum
Question Number 113745 by Algoritm last updated on 15/Sep/20
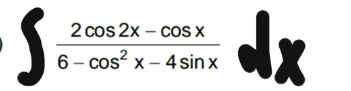
Answered by MJS_new last updated on 15/Sep/20
![((2cos 2x −cos x)/(6−cos^2 x −4sin x))= =−((cos x)/(sin^2 x −4sin x +5))+((2(2cos^2 x −1))/(sin^2 x −4sin x +5)) −∫((cos x)/(sin^2 x −4sin x +5))dx= [t=2+sin x → dx=(dt/(cos x))] =−∫(dt/(t^2 +1))=−arctan t = =−arctan (2+sin x) 2∫((2cos^2 x −1)/(sin^2 x −4sin x +5))dx= [t=tan x +(√(1+tan^2 x)) → dx=((cos^2 x)/(1+sin x))dt] (x=arctan ((t^2 −1)/(2t))) =−2∫((t^4 −6t^2 +1)/((t^2 +1)(t^4 +4t^2 +5)))dt= =−2∫((t^4 −6t^2 +1)/((t^2 +1)(t^2 −(√(−4+2(√5))) t+(√5))(t^2 +(√(−4+2(√5))) t+(√5))))dt now decompose and use the formulas for ∫((ax+b)/(x^2 +cx+d))dx. I think you should start to work for yourself now...](Q113783.png)
| ||
Question and Answers Forum | ||
Question Number 113745 by Algoritm last updated on 15/Sep/20 | ||
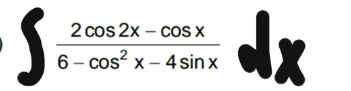 | ||
Answered by MJS_new last updated on 15/Sep/20 | ||
![((2cos 2x −cos x)/(6−cos^2 x −4sin x))= =−((cos x)/(sin^2 x −4sin x +5))+((2(2cos^2 x −1))/(sin^2 x −4sin x +5)) −∫((cos x)/(sin^2 x −4sin x +5))dx= [t=2+sin x → dx=(dt/(cos x))] =−∫(dt/(t^2 +1))=−arctan t = =−arctan (2+sin x) 2∫((2cos^2 x −1)/(sin^2 x −4sin x +5))dx= [t=tan x +(√(1+tan^2 x)) → dx=((cos^2 x)/(1+sin x))dt] (x=arctan ((t^2 −1)/(2t))) =−2∫((t^4 −6t^2 +1)/((t^2 +1)(t^4 +4t^2 +5)))dt= =−2∫((t^4 −6t^2 +1)/((t^2 +1)(t^2 −(√(−4+2(√5))) t+(√5))(t^2 +(√(−4+2(√5))) t+(√5))))dt now decompose and use the formulas for ∫((ax+b)/(x^2 +cx+d))dx. I think you should start to work for yourself now...](Q113783.png) | ||
| ||