
Question Number 113756 by Dwaipayan Shikari last updated on 15/Sep/20
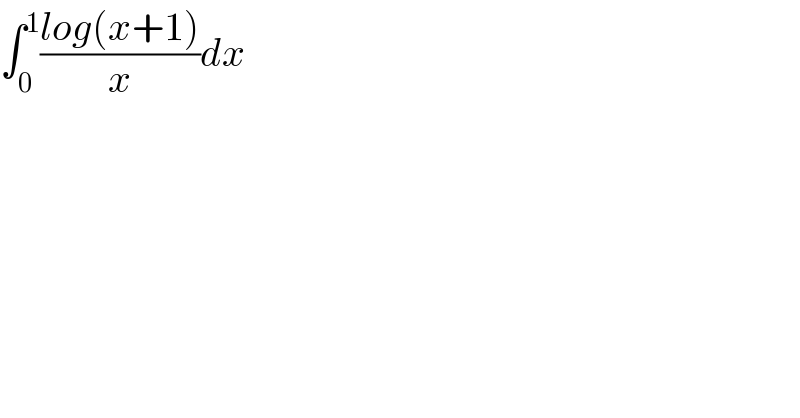
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({x}+\mathrm{1}\right)}{{x}}{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 15/Sep/20

$$\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}−\mathrm{1}} }{{n}}{dx} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}−\mathrm{1}} }{{n}}{dx} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$ \\ $$
Answered by mathdave last updated on 15/Sep/20

$${solution}\: \\ $$$${let}\:{x}=−{x} \\ $$$$\int_{\mathrm{0}} ^{−\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx}=−{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
Answered by mindispower last updated on 15/Sep/20
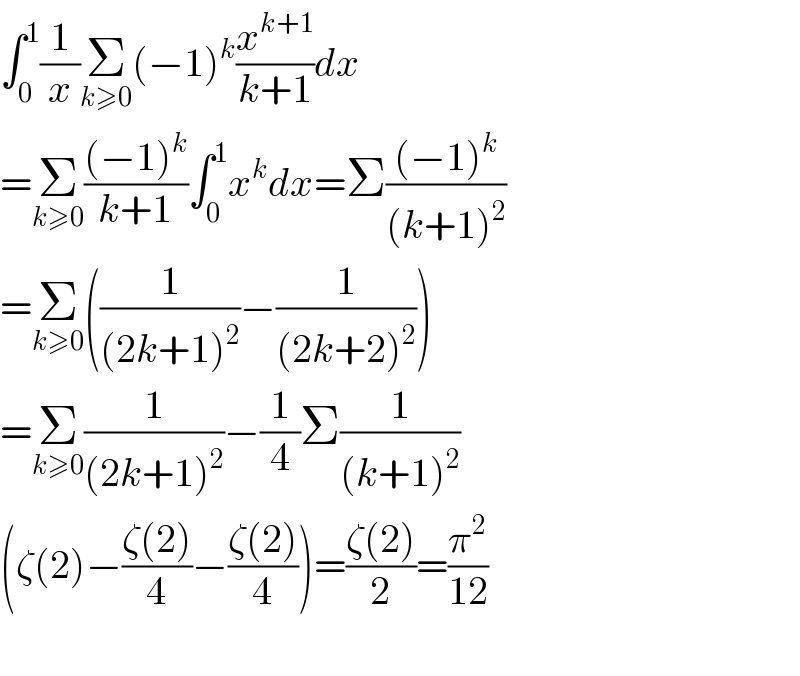
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}\underset{{k}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{k}} \frac{{x}^{{k}+\mathrm{1}} }{{k}+\mathrm{1}}{dx} \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{k}} {dx}=\Sigma\frac{\left(−\mathrm{1}\right)^{{k}} }{\left({k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\left(\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{2}\right)^{\mathrm{2}} }\right) \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4}}\Sigma\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\left(\zeta\left(\mathrm{2}\right)−\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{4}}−\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{4}}\right)=\frac{\zeta\left(\mathrm{2}\right)}{\mathrm{2}}=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$ \\ $$
