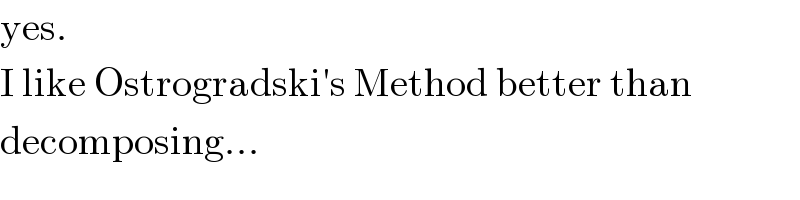Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 114056 by mathmax by abdo last updated on 16/Sep/20

calculate ∫_2 ^(+∞) (dt/((2t+3)^4 (t−1)^5 ))

$$\mathrm{calculate}\:\int_{\mathrm{2}} ^{+\infty} \:\:\:\:\frac{\mathrm{dt}}{\left(\mathrm{2t}+\mathrm{3}\right)^{\mathrm{4}} \left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{5}} } \\ $$

Answered by Olaf last updated on 17/Sep/20

R(x) = ((1/(625))/((x−1)^5 )) −((8/(3125))/((x−1)^4 )) +((8/(3135))/((x−1)^3 )) +(((32)/(15625))/((x−1)^2 )) +(((112)/(78125))/(x−1)) +(((32)/(3125))/((2x+3)^4 )) −(((32)/(3125))/((2x+3)^3 )) −(((96)/(15625))/((2x+3)^2 )) −(((225)/(78125))/(2x+3)) ∫_2 ^∞ R(x)dx = ...

$$\mathrm{R}\left({x}\right)\:=\: \\ $$$$\frac{\frac{\mathrm{1}}{\mathrm{625}}}{\left({x}−\mathrm{1}\right)^{\mathrm{5}} } \\ $$$$−\frac{\frac{\mathrm{8}}{\mathrm{3125}}}{\left({x}−\mathrm{1}\right)^{\mathrm{4}} } \\ $$$$+\frac{\frac{\mathrm{8}}{\mathrm{3135}}}{\left({x}−\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$+\frac{\frac{\mathrm{32}}{\mathrm{15625}}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$+\frac{\frac{\mathrm{112}}{\mathrm{78125}}}{{x}−\mathrm{1}} \\ $$$$+\frac{\frac{\mathrm{32}}{\mathrm{3125}}}{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{4}} } \\ $$$$−\frac{\frac{\mathrm{32}}{\mathrm{3125}}}{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{3}} } \\ $$$$−\frac{\frac{\mathrm{96}}{\mathrm{15625}}}{\left(\mathrm{2}{x}+\mathrm{3}\right)^{\mathrm{2}} } \\ $$$$−\frac{\frac{\mathrm{225}}{\mathrm{78125}}}{\mathrm{2}{x}+\mathrm{3}} \\ $$$$\int_{\mathrm{2}} ^{\infty} \mathrm{R}\left({x}\right){dx}\:=\:... \\ $$

Answered by Olaf last updated on 17/Sep/20

u = t−1 I = ∫_1 ^∞ (du/(u^5 (u+5)^4 )) x = (1/u) I = ∫_1 ^0 (x^5 /(((1/x)+5)^5 ))(−(dx/x^2 )) I = ∫_0 ^1 (x^8 /((5x+1)^5 ))dx λ = 5x+1 I = (1/5^8 )∫_1 ^6 (((λ−1)^8 )/λ^5 ).(dλ/5) I = (1/5^9 )∫_1 ^6 ((Σ_(k=0) ^8 C_8 ^k λ^k (−1)^(8−k) )/λ^5 )dλ ... may be this way is better...

$${u}\:=\:{t}−\mathrm{1} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{1}} ^{\infty} \frac{{du}}{{u}^{\mathrm{5}} \left({u}+\mathrm{5}\right)^{\mathrm{4}} } \\ $$$${x}\:=\:\frac{\mathrm{1}}{{u}} \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{1}} ^{\mathrm{0}} \frac{{x}^{\mathrm{5}} }{\left(\frac{\mathrm{1}}{{x}}+\mathrm{5}\right)^{\mathrm{5}} }\left(−\frac{{dx}}{{x}^{\mathrm{2}} }\right) \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{8}} }{\left(\mathrm{5}{x}+\mathrm{1}\right)^{\mathrm{5}} }{dx} \\ $$$$\lambda\:=\:\mathrm{5}{x}+\mathrm{1} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{8}} }\int_{\mathrm{1}} ^{\mathrm{6}} \frac{\left(\lambda−\mathrm{1}\right)^{\mathrm{8}} }{\lambda^{\mathrm{5}} }.\frac{{d}\lambda}{\mathrm{5}} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{9}} }\int_{\mathrm{1}} ^{\mathrm{6}} \frac{\underset{{k}=\mathrm{0}} {\overset{\mathrm{8}} {\sum}}\mathrm{C}_{\mathrm{8}} ^{{k}} \lambda^{{k}} \left(−\mathrm{1}\right)^{\mathrm{8}−{k}} }{\lambda^{\mathrm{5}} }{d}\lambda \\ $$$$...\:{may}\:{be}\:{this}\:{way}\:{is}\:{better}... \\ $$$$ \\ $$

Answered by 1549442205PVT last updated on 17/Sep/20

Put u=(1/(t−1))⇒du=((−1)/((t−1)^2 ))dt dt=−(t−1)^2 du=((−1)/u^2 )du,t=(1/u)+1 ∫_2 ^∞ (dt/((2t+3)^4 (t−1)^5 ))=∫_1 ^0 ((−u^3 du)/(((2/u)+5)^4 )) =−∫_1 ^0 (u^7 /((5u+2)^4 ))du=−(1/(625))∫_(7/5) ^0 (u^7 /((u+(2/5))^4 ))du Put u+(2/5)=v⇒du=dv,u=v−(2/5) I=−(1/(625))∫_(7/5) ^(2/5) (((v−(2/5))^7 )/v^4 )dv =((−1)/(625))∫_(7/5) ^(2/5) {[v^7 −7v^6 .0.4+21v^5 .0.4^2 −35v^4 .0.4^3 +35v^3 .0.4^4 −21v^2 .(0.4)^5 +7v.(0.4)^6 −(0.4)^7 ]/v^4 }dv =((−1)/(625))∫_(7/5) ^∞ [v^3 −((14)/5)v^2 +21v.((2/5))^2 −((35.8)/(125)) +((35.16)/(625v))−((21.32)/(3125v^2 ))+((7.64)/(15625v^3 ))−((128)/(5^7 v^4 ))] =((−1)/(625)){(v^4 /4)−((14v^3 )/(15))+((42)/(25))v^2 −((280)/(125))v +((560)/(625)).ln∣v∣+((672)/(3125v))−((224)/(15625v^2 ))+((128)/(3.5^7 v^3 ))]_(7/5) ^(2/5) =−(1/(625))[(−1.0449965−(−0.99590280)]= (−0.0490937)/625=0.00007855

$$\mathrm{Put}\:\mathrm{u}=\frac{\mathrm{1}}{\mathrm{t}−\mathrm{1}}\Rightarrow\mathrm{du}=\frac{−\mathrm{1}}{\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{dt}=−\left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{2}} \mathrm{du}=\frac{−\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\mathrm{du},\mathrm{t}=\frac{\mathrm{1}}{\mathrm{u}}+\mathrm{1} \\ $$$$\int_{\mathrm{2}} ^{\infty} \:\:\:\:\frac{\mathrm{dt}}{\left(\mathrm{2t}+\mathrm{3}\right)^{\mathrm{4}} \left(\mathrm{t}−\mathrm{1}\right)^{\mathrm{5}} }=\int_{\mathrm{1}} ^{\mathrm{0}} \frac{−\mathrm{u}^{\mathrm{3}} \mathrm{du}}{\left(\frac{\mathrm{2}}{\mathrm{u}}+\mathrm{5}\right)^{\mathrm{4}} } \\ $$$$=−\int_{\mathrm{1}} ^{\mathrm{0}} \frac{\mathrm{u}^{\mathrm{7}} }{\left(\mathrm{5u}+\mathrm{2}\right)^{\mathrm{4}} }\mathrm{du}=−\frac{\mathrm{1}}{\mathrm{625}}\int_{\mathrm{7}/\mathrm{5}} ^{\mathrm{0}} \frac{\mathrm{u}^{\mathrm{7}} }{\left(\mathrm{u}+\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{4}} }\mathrm{du} \\ $$$$\mathrm{Put}\:\mathrm{u}+\frac{\mathrm{2}}{\mathrm{5}}=\mathrm{v}\Rightarrow\mathrm{du}=\mathrm{dv},\mathrm{u}=\mathrm{v}−\frac{\mathrm{2}}{\mathrm{5}} \\ $$$$\mathrm{I}=−\frac{\mathrm{1}}{\mathrm{625}}\int_{\mathrm{7}/\mathrm{5}} ^{\mathrm{2}/\mathrm{5}} \frac{\left(\mathrm{v}−\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{7}} }{\mathrm{v}^{\mathrm{4}} }\mathrm{dv} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{625}}\int_{\mathrm{7}/\mathrm{5}} ^{\mathrm{2}/\mathrm{5}} \left\{\left[\mathrm{v}^{\mathrm{7}} −\mathrm{7v}^{\mathrm{6}} .\mathrm{0}.\mathrm{4}+\mathrm{21v}^{\mathrm{5}} .\mathrm{0}.\mathrm{4}^{\mathrm{2}} \right.\right. \\ $$$$−\mathrm{35v}^{\mathrm{4}} .\mathrm{0}.\mathrm{4}^{\mathrm{3}} +\mathrm{35v}^{\mathrm{3}} .\mathrm{0}.\mathrm{4}^{\mathrm{4}} −\mathrm{21v}^{\mathrm{2}} .\left(\mathrm{0}.\mathrm{4}\right)^{\mathrm{5}} \\ $$$$\left.+\left.\mathrm{7v}.\left(\mathrm{0}.\mathrm{4}\right)^{\mathrm{6}} −\left(\mathrm{0}.\mathrm{4}\right)^{\mathrm{7}} \right]/\mathrm{v}^{\mathrm{4}} \right\}\mathrm{dv} \\ $$$$=\frac{−\mathrm{1}}{\mathrm{625}}\int_{\mathrm{7}/\mathrm{5}} ^{\infty} \left[\mathrm{v}^{\mathrm{3}} −\frac{\mathrm{14}}{\mathrm{5}}\mathrm{v}^{\mathrm{2}} +\mathrm{21v}.\left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{2}} −\frac{\mathrm{35}.\mathrm{8}}{\mathrm{125}}\right. \\ $$$$\left.+\frac{\mathrm{35}.\mathrm{16}}{\mathrm{625v}}−\frac{\mathrm{21}.\mathrm{32}}{\mathrm{3125v}^{\mathrm{2}} }+\frac{\mathrm{7}.\mathrm{64}}{\mathrm{15625v}^{\mathrm{3}} }−\frac{\mathrm{128}}{\mathrm{5}^{\mathrm{7}} \mathrm{v}^{\mathrm{4}} }\right] \\ $$$$=\frac{−\mathrm{1}}{\mathrm{625}}\left\{\frac{\mathrm{v}^{\mathrm{4}} }{\mathrm{4}}−\frac{\mathrm{14v}^{\mathrm{3}} }{\mathrm{15}}+\frac{\mathrm{42}}{\mathrm{25}}\mathrm{v}^{\mathrm{2}} −\frac{\mathrm{280}}{\mathrm{125}}\mathrm{v}\right. \\ $$$$\left.+\frac{\mathrm{560}}{\mathrm{625}}.\mathrm{ln}\mid\mathrm{v}\mid+\frac{\mathrm{672}}{\mathrm{3125v}}−\frac{\mathrm{224}}{\mathrm{15625v}^{\mathrm{2}} }+\frac{\mathrm{128}}{\mathrm{3}.\mathrm{5}^{\mathrm{7}} \mathrm{v}^{\mathrm{3}} }\right]_{\mathrm{7}/\mathrm{5}} ^{\mathrm{2}/\mathrm{5}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{625}}\left[\left(−\mathrm{1}.\mathrm{0449965}−\left(−\mathrm{0}.\mathrm{99590280}\right)\right]=\right. \\ $$$$\left(−\mathrm{0}.\mathrm{0490937}\right)/\mathrm{625}=\mathrm{0}.\mathrm{00007855} \\ $$$$ \\ $$

Answered by MJS_new last updated on 17/Sep/20

∫(dt/((2t+3)^4 (t−1)^5 ))= [Ostrogradski′s Method] =((5376t^6 +1344t^5 −25760t^4 +3080t^3 +40740t^2 −17906t−16249)/(187500(t−1)^4 (2t+3)^3 ))+ +((112)/(15625))∫(dt/((t−1)(2t+3))) this integral=((112)/(78125))ln ∣((t−1)/(2t+3))∣ ⇒ answer is ((112)/(78125))(ln 7 −ln 2)−((36817)/(21437500))

$$\int\frac{{dt}}{\left(\mathrm{2}{t}+\mathrm{3}\right)^{\mathrm{4}} \left({t}−\mathrm{1}\right)^{\mathrm{5}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{\mathrm{5376}{t}^{\mathrm{6}} +\mathrm{1344}{t}^{\mathrm{5}} −\mathrm{25760}{t}^{\mathrm{4}} +\mathrm{3080}{t}^{\mathrm{3}} +\mathrm{40740}{t}^{\mathrm{2}} −\mathrm{17906}{t}−\mathrm{16249}}{\mathrm{187500}\left({t}−\mathrm{1}\right)^{\mathrm{4}} \left(\mathrm{2}{t}+\mathrm{3}\right)^{\mathrm{3}} }+ \\ $$$$+\frac{\mathrm{112}}{\mathrm{15625}}\int\frac{{dt}}{\left({t}−\mathrm{1}\right)\left(\mathrm{2}{t}+\mathrm{3}\right)} \\ $$$$\mathrm{this}\:\mathrm{integral}=\frac{\mathrm{112}}{\mathrm{78125}}\mathrm{ln}\:\mid\frac{{t}−\mathrm{1}}{\mathrm{2}{t}+\mathrm{3}}\mid \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{112}}{\mathrm{78125}}\left(\mathrm{ln}\:\mathrm{7}\:−\mathrm{ln}\:\mathrm{2}\right)−\frac{\mathrm{36817}}{\mathrm{21437500}} \\ $$

Commented by 1549442205PVT last updated on 17/Sep/20

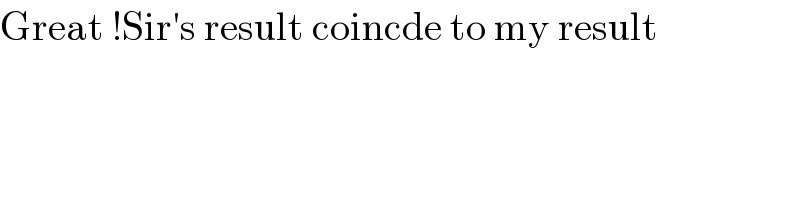
Great !Sir′s result coincde to my result

$$\mathrm{Great}\:!\mathrm{Sir}'\mathrm{s}\:\mathrm{result}\:\mathrm{coincde}\:\mathrm{to}\:\mathrm{my}\:\mathrm{result} \\ $$

Commented by MJS_new last updated on 17/Sep/20

yes. I like Ostrogradski′s Method better than decomposing...

$$\mathrm{yes}. \\ $$$$\mathrm{I}\:\mathrm{like}\:\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\:\mathrm{better}\:\mathrm{than} \\ $$$$\mathrm{decomposing}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com