Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 114185 by mohammad17 last updated on 17/Sep/20

Answered by Dwaipayan Shikari last updated on 17/Sep/20

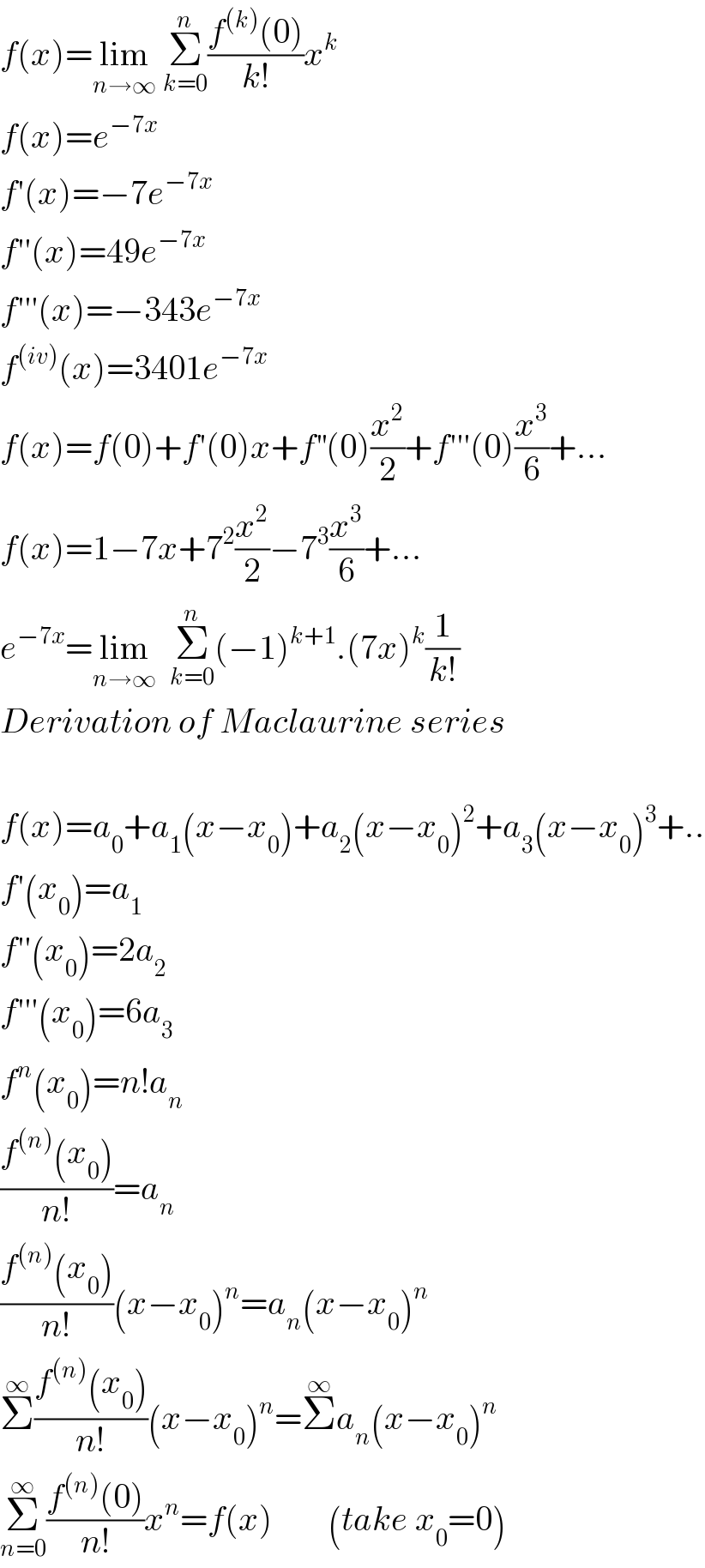
f(x)=lim_(n→∞) Σ_(k=0) ^n ((f^((k)) (0))/(k!))x^k f(x)=e^(−7x) f′(x)=−7e^(−7x) f′′(x)=49e^(−7x) f′′′(x)=−343e^(−7x) f^((iv)) (x)=3401e^(−7x) f(x)=f(0)+f′(0)x+f^(′′) (0)(x^2 /2)+f′′′(0)(x^3 /6)+... f(x)=1−7x+7^2 (x^2 /2)−7^3 (x^3 /6)+... e^(−7x) =lim_(n→∞) Σ_(k=0) ^n (−1)^(k+1) .(7x)^k (1/(k!)) Derivation of Maclaurine series f(x)=a_0 +a_1 (x−x_0 )+a_2 (x−x_0 )^2 +a_3 (x−x_0 )^3 +.. f′(x_0 )=a_1 f′′(x_0 )=2a_2 f′′′(x_0 )=6a_3 f^n (x_0 )=n!a_n ((f^((n)) (x_0 ))/(n!))=a_n ((f^((n)) (x_0 ))/(n!))(x−x_0 )^n =a_n (x−x_0 )^n Σ^∞ ((f^((n)) (x_0 ))/(n!))(x−x_0 )^n =Σ^∞ a_n (x−x_0 )^n Σ_(n=0) ^∞ ((f^((n)) (0))/(n!))x^n =f(x) (take x_0 =0)

$${f}\left({x}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{f}^{\left({k}\right)} \left(\mathrm{0}\right)}{{k}!}{x}^{{k}} \\ $$$${f}\left({x}\right)={e}^{−\mathrm{7}{x}} \\ $$$${f}'\left({x}\right)=−\mathrm{7}{e}^{−\mathrm{7}{x}} \\ $$$${f}''\left({x}\right)=\mathrm{49}{e}^{−\mathrm{7}{x}} \\ $$$${f}'''\left({x}\right)=−\mathrm{343}{e}^{−\mathrm{7}{x}} \\ $$$${f}^{\left({iv}\right)} \left({x}\right)=\mathrm{3401}{e}^{−\mathrm{7}{x}} \\ $$$${f}\left({x}\right)={f}\left(\mathrm{0}\right)+{f}'\left(\mathrm{0}\right){x}+{f}^{''} \left(\mathrm{0}\right)\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{f}'''\left(\mathrm{0}\right)\frac{{x}^{\mathrm{3}} }{\mathrm{6}}+... \\ $$$${f}\left({x}\right)=\mathrm{1}−\mathrm{7}{x}+\mathrm{7}^{\mathrm{2}} \frac{{x}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{7}^{\mathrm{3}} \frac{{x}^{\mathrm{3}} }{\mathrm{6}}+... \\ $$$${e}^{−\mathrm{7}{x}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} .\left(\mathrm{7}{x}\right)^{{k}} \frac{\mathrm{1}}{{k}!} \\ $$$${Derivation}\:{of}\:{Maclaurine}\:{series} \\ $$$$ \\ $$$${f}\left({x}\right)={a}_{\mathrm{0}} +{a}_{\mathrm{1}} \left({x}−{x}_{\mathrm{0}} \right)+{a}_{\mathrm{2}} \left({x}−{x}_{\mathrm{0}} \right)^{\mathrm{2}} +{a}_{\mathrm{3}} \left({x}−{x}_{\mathrm{0}} \right)^{\mathrm{3}} +.. \\ $$$${f}'\left({x}_{\mathrm{0}} \right)={a}_{\mathrm{1}} \\ $$$${f}''\left({x}_{\mathrm{0}} \right)=\mathrm{2}{a}_{\mathrm{2}} \\ $$$${f}'''\left({x}_{\mathrm{0}} \right)=\mathrm{6}{a}_{\mathrm{3}} \\ $$$${f}^{{n}} \left({x}_{\mathrm{0}} \right)={n}!{a}_{{n}} \\ $$$$\frac{{f}^{\left({n}\right)} \left({x}_{\mathrm{0}} \right)}{{n}!}={a}_{{n}} \\ $$$$\frac{{f}^{\left({n}\right)} \left({x}_{\mathrm{0}} \right)}{{n}!}\left({x}−{x}_{\mathrm{0}} \right)^{{n}} ={a}_{{n}} \left({x}−{x}_{\mathrm{0}} \right)^{{n}} \\ $$$$\overset{\infty} {\sum}\frac{{f}^{\left({n}\right)} \left({x}_{\mathrm{0}} \right)}{{n}!}\left({x}−{x}_{\mathrm{0}} \right)^{{n}} =\overset{\infty} {\sum}{a}_{{n}} \left({x}−{x}_{\mathrm{0}} \right)^{{n}} \\ $$$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{f}^{\left({n}\right)} \left(\mathrm{0}\right)}{{n}!}{x}^{{n}} ={f}\left({x}\right)\:\:\:\:\:\:\:\:\left({take}\:{x}_{\mathrm{0}} =\mathrm{0}\right) \\ $$

Answered by Dwaipayan Shikari last updated on 18/Sep/20

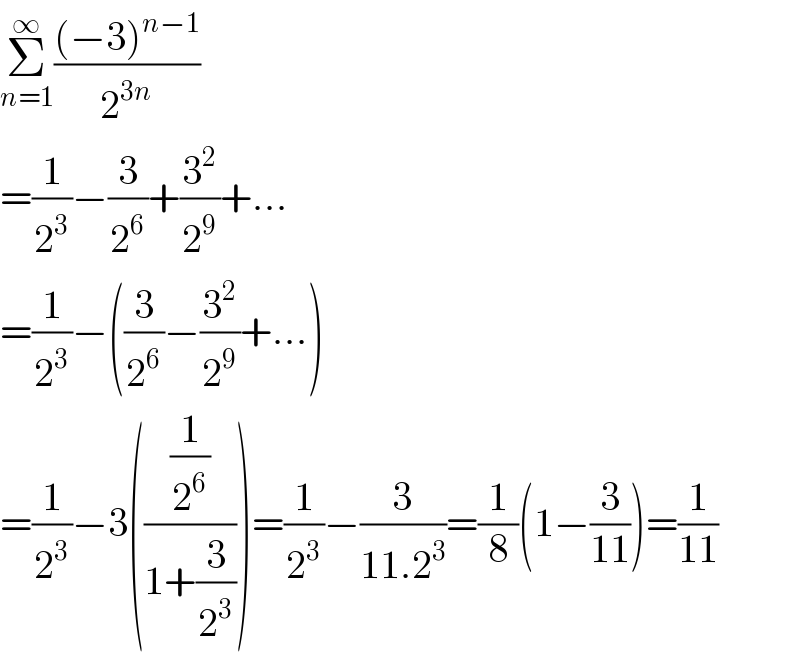
Σ_(n=1) ^∞ (((−3)^(n−1) )/2^(3n) ) =(1/2^3 )−(3/2^6 )+(3^2 /2^9 )+... =(1/2^3 )−((3/2^6 )−(3^2 /2^9 )+...) =(1/2^3 )−3(((1/2^6 )/(1+(3/2^3 ))))=(1/2^3 )−(3/(11.2^3 ))=(1/8)(1−(3/(11)))=(1/(11))

$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{3}\right)^{{n}−\mathrm{1}} }{\mathrm{2}^{\mathrm{3}{n}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }−\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{6}} }+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{9}} }+... \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }−\left(\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{6}} }−\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{9}} }+...\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }−\mathrm{3}\left(\frac{\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }}\right)=\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }−\frac{\mathrm{3}}{\mathrm{11}.\mathrm{2}^{\mathrm{3}} }=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{11}}\right)=\frac{\mathrm{1}}{\mathrm{11}} \\ $$

Answered by mathmax by abdo last updated on 17/Sep/20

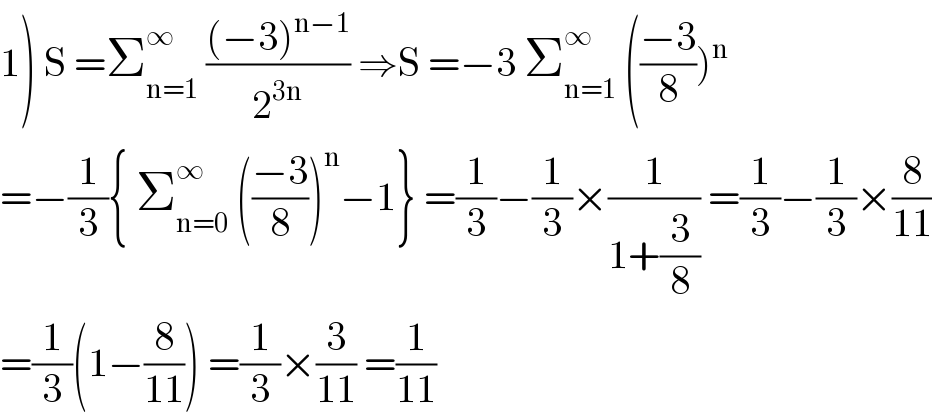
1) S =Σ_(n=1) ^∞ (((−3)^(n−1) )/2^(3n) ) ⇒S =−3 Σ_(n=1) ^∞ (((−3)/8))^n =−(1/3){ Σ_(n=0) ^∞ (((−3)/8))^n −1} =(1/3)−(1/3)×(1/(1+(3/8))) =(1/3)−(1/3)×(8/(11)) =(1/3)(1−(8/(11))) =(1/3)×(3/(11)) =(1/(11))

$$\left.\mathrm{1}\right)\:\mathrm{S}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{3}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{2}^{\mathrm{3n}} }\:\Rightarrow\mathrm{S}\:=−\mathrm{3}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\left(\frac{−\mathrm{3}}{\mathrm{8}}\right)^{\mathrm{n}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{3}}\left\{\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(\frac{−\mathrm{3}}{\mathrm{8}}\right)^{\mathrm{n}} −\mathrm{1}\right\}\:=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{8}}}\:=\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{8}}{\mathrm{11}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{8}}{\mathrm{11}}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{11}}\:=\frac{\mathrm{1}}{\mathrm{11}} \\ $$

Answered by mathmax by abdo last updated on 17/Sep/20

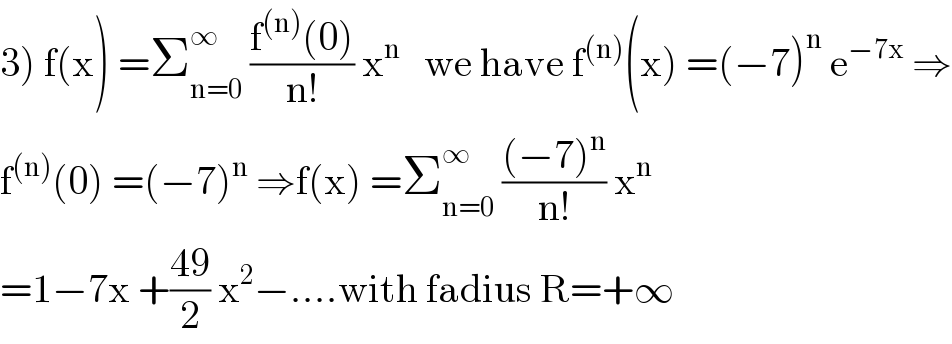
3) f(x) =Σ_(n=0) ^∞ ((f^((n)) (0))/(n!)) x^n we have f^((n)) (x) =(−7)^n e^(−7x) ⇒ f^((n)) (0) =(−7)^n ⇒f(x) =Σ_(n=0) ^∞ (((−7)^n )/(n!)) x^n =1−7x +((49)/2) x^2 −....with fadius R=+∞

$$\left.\mathrm{3}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)}{\mathrm{n}!}\:\mathrm{x}^{\mathrm{n}} \:\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\left(−\mathrm{7}\right)^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{7x}} \:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:=\left(−\mathrm{7}\right)^{\mathrm{n}} \:\Rightarrow\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{7}\right)^{\mathrm{n}} }{\mathrm{n}!}\:\mathrm{x}^{\mathrm{n}} \\ $$$$=\mathrm{1}−\mathrm{7x}\:+\frac{\mathrm{49}}{\mathrm{2}}\:\mathrm{x}^{\mathrm{2}} −....\mathrm{with}\:\mathrm{fadius}\:\mathrm{R}=+\infty \\ $$

Answered by mathmax by abdo last updated on 17/Sep/20

2) let u_n (x) =((2^n (x−2)^n )/((n+2)!)) ⇒∣((u_(n+1) (x))/(u_n (x)))∣ =∣(((2(x−2))^(n+1) )/((n+3)!))×(((n+2)!)/((2(x−2))^n ))∣ =∣(((n+2)!)/((n+3)!))×2(x−2)∣ =∣((2(x−2))/(n+3))∣→0 (n→+∞) ⇒the interval of cv is R (radius R =+∞)

$$\left.\mathrm{2}\right)\:\mathrm{let}\:\mathrm{u}_{\mathrm{n}} \left(\mathrm{x}\right)\:=\frac{\mathrm{2}^{\mathrm{n}} \left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{n}} }{\left(\mathrm{n}+\mathrm{2}\right)!}\:\Rightarrow\mid\frac{\mathrm{u}_{\mathrm{n}+\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{u}_{\mathrm{n}} \left(\mathrm{x}\right)}\mid \\ $$$$=\mid\frac{\left(\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)\right)^{\mathrm{n}+\mathrm{1}} }{\left(\mathrm{n}+\mathrm{3}\right)!}×\frac{\left(\mathrm{n}+\mathrm{2}\right)!}{\left(\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)\right)^{\mathrm{n}} }\mid\:=\mid\frac{\left(\mathrm{n}+\mathrm{2}\right)!}{\left(\mathrm{n}+\mathrm{3}\right)!}×\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)\mid \\ $$$$=\mid\frac{\mathrm{2}\left(\mathrm{x}−\mathrm{2}\right)}{\mathrm{n}+\mathrm{3}}\mid\rightarrow\mathrm{0}\:\left(\mathrm{n}\rightarrow+\infty\right)\:\Rightarrow\mathrm{the}\:\mathrm{interval}\:\mathrm{of}\:\mathrm{cv}\:\mathrm{is}\:\mathrm{R} \\ $$$$\left(\mathrm{radius}\:\mathrm{R}\:=+\infty\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com