
Question and Answers Forum
Question Number 114302 by mnjuly1970 last updated on 18/Sep/20
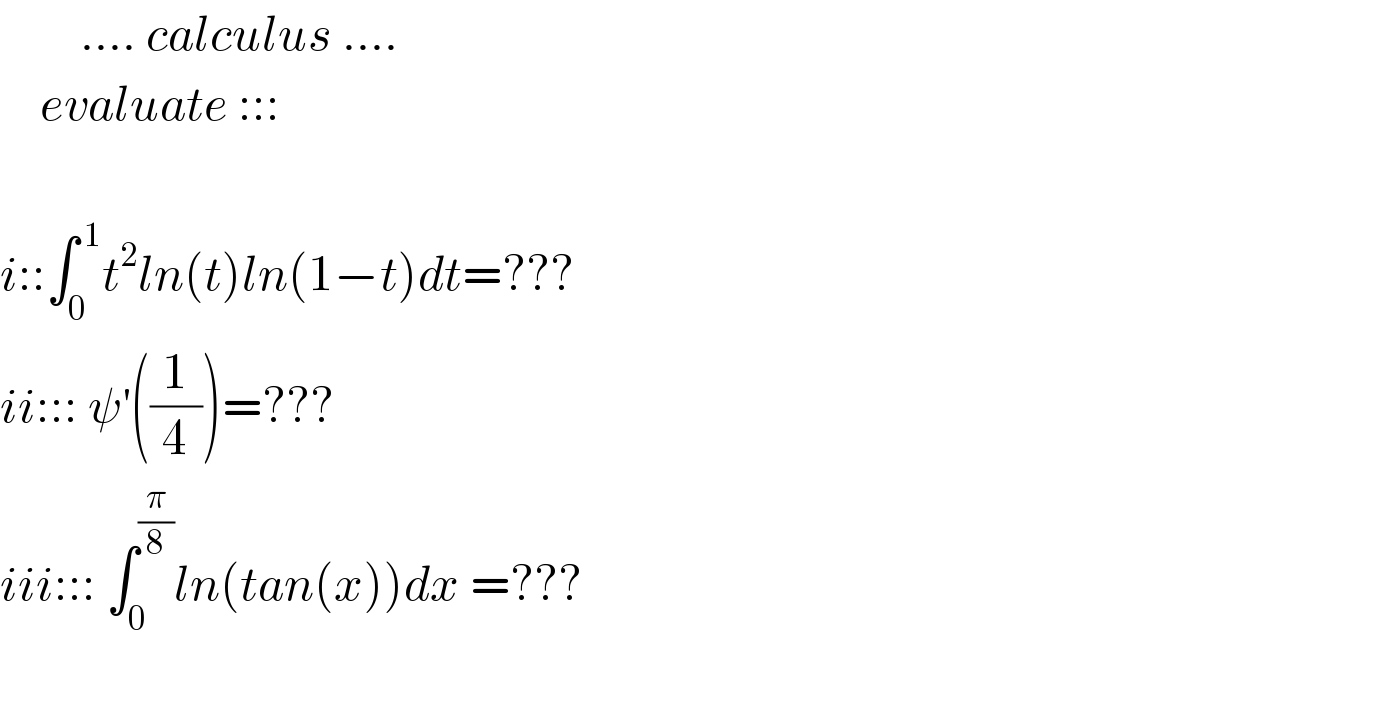
Commented by MJS_new last updated on 18/Sep/20

Commented by MJS_new last updated on 18/Sep/20
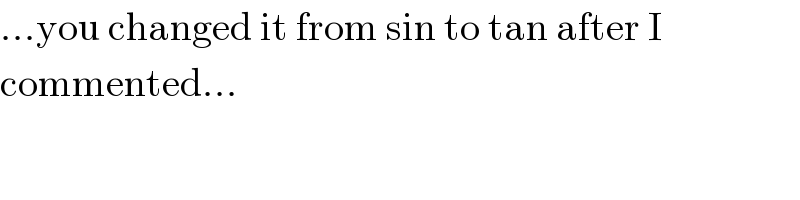
Answered by Olaf last updated on 18/Sep/20
![I_n = ∫_0 ^1 x^n lnxdx I_n = [(x^(n+1) /(n+1))lnx]_0 ^1 − ∫_0 ^1 (x^(n+1) /(n+1)).(dx/x) I_n = −[(x^(n+1) /((n+1)^2 ))]_0 ^1 = −(1/((n+1)^2 )) (1/(1−t)) = Σ_(n=0) ^∞ t^n ln∣1−t∣ = −Σ_(n=0) ^∞ (t^(n+1) /(n+1)) if ∣t∣<1 I = ∫_0 ^1 t^2 ln(t)ln(1−t)dt I = −∫_0 ^1 t^2 ln(t)Σ_(n=0) ^∞ (t^(n+1) /(n+1))dt I = −Σ_(n=0) ^∞ (1/(n+1))∫_0 ^1 t^(n+3) lntdt I = −Σ_(n=0) ^∞ (I_(n+3) /(n+1)) = Σ_(n=0) ^∞ (1/((n+1)(n+4)^2 )) I = Σ_(n=1) ^∞ (1/(n(n+3)^2 )) (1/(n(n+3)^2 )) = (1/(9n))−(1/(9(n+3)))−(1/(3(n+3)^2 )) I = (1/9)((1/1)+(1/2)+(1/3))−(1/3)Σ_(n=1() ^∞ (1/(n+3)^2 )) I = ((11)/(54))−(1/3)Σ_(n=4) ^∞ (1/n^2 ) With Σ_(n=1) ^∞ (1/n^2 ) = ξ(2) = (π^2 /6) I = ((11)/(54))−(1/3)((π^2 /6)−(1/1^2 )−(1/2^2 )−(1/3^2 )) I = ((71)/(108))−(π^2 /(18)) ≈ 0,109096051](Q114382.png)
Commented by mnjuly1970 last updated on 19/Sep/20

Answered by mathmax by abdo last updated on 19/Sep/20
![3) I =∫_0 ^(π/8) ln(tanx)dx by parts I= [xln(tanx)]_0 ^(π/8) −∫_0 ^(π/8) x×((1+tan^2 x)/(tanx))dx =(π/8)ln((√2)−1)−∫_0 ^(π/8) (x/(tanx))dx−∫_0 ^(π/8) tanx dx ∫_0 ^(π/8) tanx dx =[−ln∣cosx∣]_0 ^(π/8) =−ln(((√2)/2)) =−ln((1/(√2))) =((ln2)/2) A =∫_0 ^(π/8) (x/(tanx))dx ⇒ A =_(tanx=t) ∫_0 ^((√2)−1) ((arctant)/t)(dt/(1+t^2 )) =∫_0 ^((√2)−1) arctan(t){(1/t)−(t/(1+t^2 ))}dt =∫_0 ^((√2)−1) ((arctant)/t)dt −∫_0 ^((√2)−1) (t/(1+t^2 )) arctan(t)dt by parts ∫_0 ^((√2)−1) (t/(1+t^2 )) arctan(t)dt =[(1/2)ln(1+t^2 )arctant]_0 ^((√2)−1) −∫_0 ^((√2)−1) (1/2)ln(1+t^2 )×(dt/(1+t^2 )) =(1/2)ln(4−2(√2)) arctan((√2)−1) −(1/2) ∫_0 ^((√2)−1) ((ln(1+t^2 ))/(1+t^2 )) dt we considere f(a) =∫_0 ^((√2)−1) ((ln(1+at^2 ))/(1+t^2 ))dt with a>0 f^′ (a) =∫_0 ^((√2)−1) (t^2 /((1+t^2 )(1+at^2 ))) dt let decompose F(t) =(t^2 /((t^2 +1)(at^2 +1))) ⇒F(t)=((αt +β)/(t^2 +1)) +((mt+n)/(at^2 +1)) ⇒ F(−t)=F(t) ⇒((−αt +β)/(t^2 +1)) +((−mt +n)/(at^2 +1)) =F(t)⇒α=m=0 ⇒ F(t)=(β/(t^2 +1)) +(n/(at^2 +1)) we haveF(0) =0 =β+n ⇒n=−β lim_(t→+∞) t^2 F(t) =(1/a) =β +(n/a) ⇒1=aβ +n ⇒1=aβ−β =(a−1)β ⇒β =(1/(a−1)) ⇒F(t) =(1/((a−1)(t^2 +1)))−(1/((a−1)(at^2 +1))) ⇒ f^′ (a) =(1/(a−1)) ∫_0 ^((√2)−1) (dt/(t^2 +1))−(1/(a−1))∫_0 ^((√2)−1 ) (dt/(at^2 +1))(→(√a)t =u) =((arctan((√2)−1))/(a−1))−(1/(a−1)) ∫_0 ^(((√2)−1)(√a)) (du/((√a)(u^2 +1))) =((arctan((√2)−1))/(a−1))−(1/((√a)(a−1)))arctan(((√2)−1)(√a)) ⇒ f(a) =arctan((√2)−1)ln∣a−1∣−∫ ((arctan(((√2)−1)(√a)))/((√a)(a−1))) da +C ....be continued...](Q114396.png)
Answered by maths mind last updated on 19/Sep/20

Commented by mnjuly1970 last updated on 19/Sep/20

Answered by Olaf last updated on 19/Sep/20
![iii... I = ∫_0 ^(π/8) ln(tanx)dx tan2θ = ((2tanθ)/(1−tan^2 θ)) with θ = (π/8), tan(π/4) = ((2tan(π/8))/(1−tan^2 (π/8))) = 1 tan^2 (π/8)+2tan(π/8)−1 = 0 ⇒ tan(π/8) = (√2)−1 Now u = tanx du = (1+tan^2 x)dx = (1+u^2 )dx I = ∫_0 ^((√2)−1) ((lnu)/(1+u^2 ))du I = ∫_0 ^((√2)−1) lnuΣ_(n=0) ^∞ (−1)^n u^(2n) du I = Σ_(n=0) ^∞ (−1)^n ∫_0 ^((√2)−1) u^(2n) lnudu I = Σ_(n=0) ^∞ (−1)^n ([(u^(2n+1) /(2n+1))lnu]_0 ^((√2)−1) −∫_0 ^((√2)−1) (u^(2n+1) /(2n+1)).(du/u)) I = Σ_(n=0) ^∞ (−1)^n (ln((√2)−1)[((((√2)−1)^(2n+1) )/(2n+1))]−[(u^(2n+1) /((2n+1)^2 ))]_0 ^((√2)−1) ) I = Σ_(n=0) ^∞ (−1)^n (ln((√2)−1)[((((√2)−1)^(2n+1) )/(2n+1))]−[((((√2)−1)^(2n+1) )/((2n+1)^2 ))]) arctanx = Σ_(n=0) ^∞ (−1)^n (x^(2n+1) /(2n+1)) I = ln((√2)−1)arctan((√2)−1)−Σ_(n=0) ^∞ (−1)^n ((((√2)−1)^(2n+1) )/((2n+1)^2 )) I = (π/8)ln((√2)−1)−Σ_(n=0) ^∞ (−1)^n ((((√2)−1)^(2n+1) )/((2n+1)^2 )) I think we cannot simplify](Q114563.png)
Answered by mathmax by abdo last updated on 20/Sep/20
![A =∫_0 ^1 x^2 ln(x)ln(1−x)dx we have (d/dx)ln(1−x) =((−1)/(1−x))=−Σ_(n=0) ^∞ x^n ⇒ln(1−x) =−Σ_(n=0) ^∞ (x^(n+1) /(n+1)) +c (c=0) =−Σ_(n=1) ^∞ (x^n /n) ⇒ A =−∫_0 ^1 x^2 lnx(Σ_(n=1) ^∞ (x^n /n))dx =−Σ_(n=1) ^∞ (1/n) ∫_0 ^1 x^(n+2) ln(x)dx u_n =∫_0 ^1 x^(n+2) ln(x)dx =[(x^(n+3) /(n+3))ln(x)]_0 ^1 −∫_0 ^1 (x^(n+2) /(n+3)) dx =−(1/((n+3)^2 )) ⇒ A =Σ_(n=1) ^∞ (1/(n(n+3)^2 )) let decompose F(x) =(1/(x(x+3)^2 )) ⇒F(x) =(a/x) +(b/(x+3)) +(c/((x+3)^2 )) a=(1/9) , c =−(1/3) ⇒F(x) =(1/(9x)) +(b/(x+3))−(1/(3(x+3)^2 )) lim_(x→+∞) xF(x) =0 =(1/9) +b ⇒b=−(1/9) ⇒ A =lim_(n→+∞) A_n / A_n =Σ_(k=1) ^n (1/(k(k+3)^2 )) =(1/9) Σ_(k=1) ^n (1/k)−(1/9)Σ_(k=1) ^n (1/(k+3))−(1/3) Σ_(k=1) ^n (1/((k+3)^2 )) =(1/9)Σ_(k=1) ^n (1/k)−(1/9) Σ_(k=4) ^(n+3) −(1/3)Σ_(k=4) ^(n+3) (1/k^2 ) =(1/9)(1 +(1/2)+(1/3))−(1/9)((1/(n+1))+(1/(n+2))+(1/(n+3)))−(1/3)(Σ_(k=1) ^(n+3) (1/k^2 )−1−(1/2^2 )−(1/3^2 )) →(1/9)((3/2)+(1/3))−(1/3)×(π^2 /6) +(1/3)(1+(1/4)+(1/9)) =(1/9)(((11)/6))−(π^2 /(18)) +(1/3)((5/4)+(1/9)) =((11)/(54))−(π^2 /(18))+(1/3)(((49)/(36))) =((11)/(54))+((49)/(108))−(π^2 /(18)) ⇒∫_0 ^1 x^2 lnx ln(1−x)dx =((11)/(54))+((49)/(108))−(π^2 /(18))](Q114632.png)
Commented by mathmax by abdo last updated on 20/Sep/20
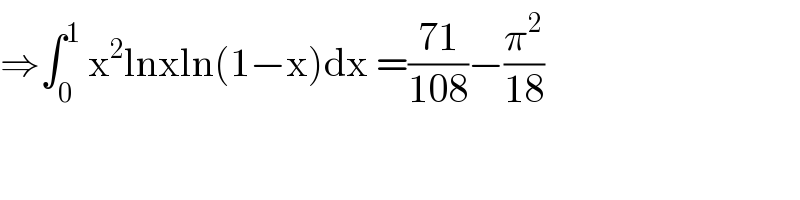
Answered by maths mind last updated on 20/Sep/20
![Ψ_1 ((1/4))=∫_0 ^∞ ((ln(x)x^(−(3/4)) )/(x−1))dx x^(1/4) =t⇒dt=((x^(−(3/4)) dx)/4) =∫_0 ^∞ ((4ln(t^4 ))/(t^4 −1))dt =16∫_0 ^1 ((ln(t))/((t^2 −1)(t^2 +1)))dt =8∫_0 ^1 ((ln(t))/(t^2 −1))−∫_0 ^1 ((ln(t))/(t^2 +1)) =−8∫_0 ^1 Σ_(k≥0) t^(2k) ln(t)dt−8Σ_(m≥0) ∫_0 ^1 (−t^2 )^m ln(t)dt =−8Σ_(k≥0) ∫_0 ^1 t^(2k) ln(t)dt−8Σ(−1)^m ∫_0 ^1 t^(2m) ln(t)dt ∫_0 ^1 t^n ln(t)=[((t^(n+1) ln(t))/(n+1))]_0 ^1 −∫(t^n /(n+1))dt=−(1/((n+1)^2 )) =8Σ_(k≥0) (1/((2k+1)^2 ))+8.Σ(((−1)^k )/((2k+1)^2 )) =8.(3/4)ζ(2)+8.G =π^2 +8G](Q114729.png)
