Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 114347 by mohammad17 last updated on 18/Sep/20

if (x^2 −(h+1)x+6i−6=0) then find the value of h if you know that one of the roots of the equation is three times the square of the other root (h∈ complex number)

$$\:{if}\:\left({x}^{\mathrm{2}} −\left({h}+\mathrm{1}\right){x}+\mathrm{6}{i}−\mathrm{6}=\mathrm{0}\right)\:{then}\:{find}\:{the}\:{value}\:{of}\:{h} \\ $$$${if}\:{you}\:{know}\:{that}\:{one}\:{of}\:{the}\:{roots}\:{of}\:{the}\:{equation}\:{is}\:{three}\: \\ $$$${times}\:{the}\:{square}\:{of}\:{the}\:{other}\:{root}\: \\ $$$$\left({h}\in\:{complex}\:{number}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Answered by Olaf last updated on 18/Sep/20

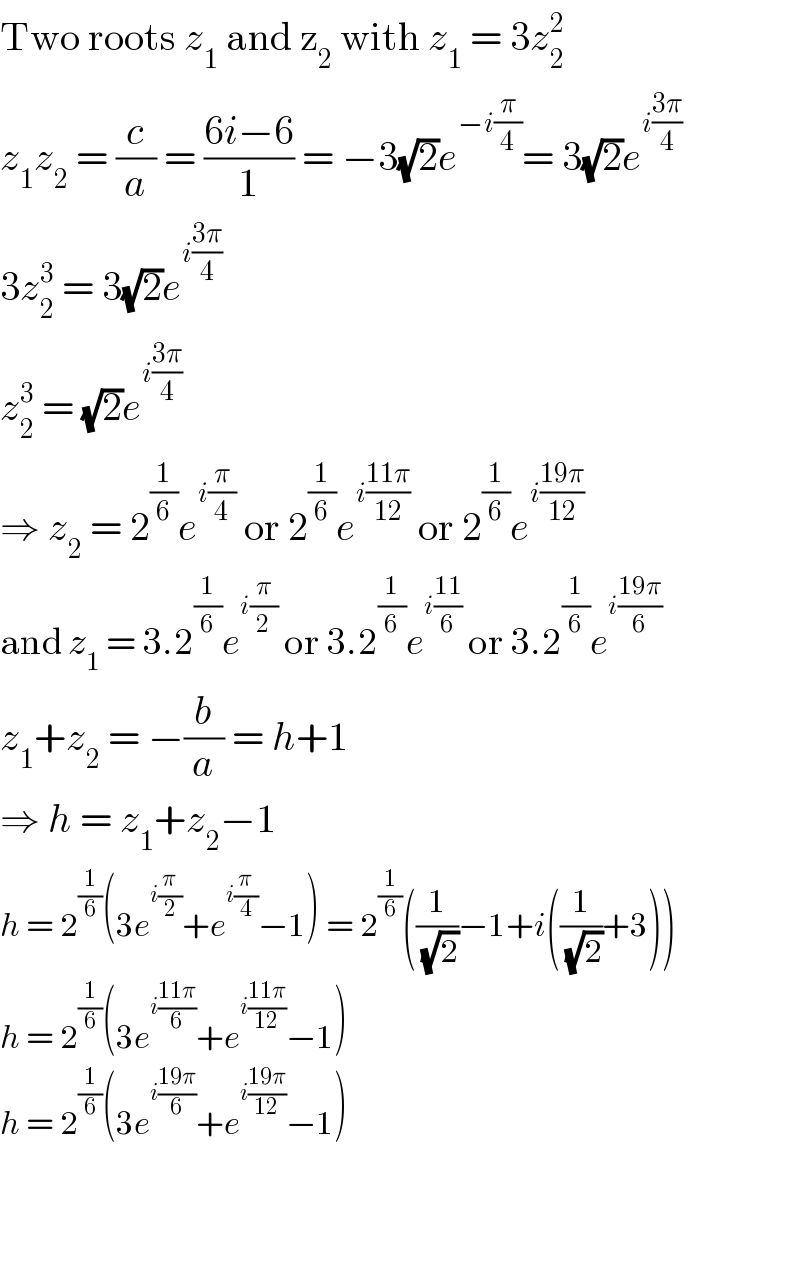
Two roots z_1 and z_2 with z_1 = 3z_2 ^2 z_1 z_2 = (c/a) = ((6i−6)/1) = −3(√2)e^(−i(π/4)) = 3(√2)e^(i((3π)/4)) 3z_2 ^3 = 3(√2)e^(i((3π)/4)) z_2 ^3 = (√2)e^(i((3π)/4)) ⇒ z_2 = 2^(1/6) e^(i(π/4)) or 2^(1/6) e^(i((11π)/(12))) or 2^(1/6) e^(i((19π)/(12))) and z_1 = 3.2^(1/6) e^(i(π/2)) or 3.2^(1/6) e^(i((11)/6)) or 3.2^(1/6) e^(i((19π)/6)) z_1 +z_2 = −(b/a) = h+1 ⇒ h = z_1 +z_2 −1 h = 2^(1/6) (3e^(i(π/2)) +e^(i(π/4)) −1) = 2^(1/6) ((1/( (√2)))−1+i((1/( (√2)))+3)) h = 2^(1/6) (3e^(i((11π)/6)) +e^(i((11π)/(12))) −1) h = 2^(1/6) (3e^(i((19π)/6)) +e^(i((19π)/(12))) −1)

$$\mathrm{Two}\:\mathrm{roots}\:{z}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{z}_{\mathrm{2}} \:\mathrm{with}\:{z}_{\mathrm{1}} \:=\:\mathrm{3}{z}_{\mathrm{2}} ^{\mathrm{2}} \\ $$$${z}_{\mathrm{1}} {z}_{\mathrm{2}} \:=\:\frac{{c}}{{a}}\:=\:\frac{\mathrm{6}{i}−\mathrm{6}}{\mathrm{1}}\:=\:−\mathrm{3}\sqrt{\mathrm{2}}{e}^{−{i}\frac{\pi}{\mathrm{4}}} =\:\mathrm{3}\sqrt{\mathrm{2}}{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \\ $$$$\mathrm{3}{z}_{\mathrm{2}} ^{\mathrm{3}} \:=\:\mathrm{3}\sqrt{\mathrm{2}}{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \\ $$$${z}_{\mathrm{2}} ^{\mathrm{3}} \:=\:\sqrt{\mathrm{2}}{e}^{{i}\frac{\mathrm{3}\pi}{\mathrm{4}}} \\ $$$$\Rightarrow\:{z}_{\mathrm{2}} \:=\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} {e}^{{i}\frac{\pi}{\mathrm{4}}} \:\mathrm{or}\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} {e}^{{i}\frac{\mathrm{11}\pi}{\mathrm{12}}} \:\mathrm{or}\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} {e}^{{i}\frac{\mathrm{19}\pi}{\mathrm{12}}} \\ $$$$\mathrm{and}\:{z}_{\mathrm{1}} \:=\:\mathrm{3}.\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} {e}^{{i}\frac{\pi}{\mathrm{2}}} \:\mathrm{or}\:\mathrm{3}.\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} {e}^{{i}\frac{\mathrm{11}}{\mathrm{6}}} \:\mathrm{or}\:\mathrm{3}.\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} {e}^{{i}\frac{\mathrm{19}\pi}{\mathrm{6}}} \\ $$$${z}_{\mathrm{1}} +{z}_{\mathrm{2}} \:=\:−\frac{{b}}{{a}}\:=\:{h}+\mathrm{1} \\ $$$$\Rightarrow\:{h}\:=\:{z}_{\mathrm{1}} +{z}_{\mathrm{2}} −\mathrm{1} \\ $$$${h}\:=\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} \left(\mathrm{3}{e}^{{i}\frac{\pi}{\mathrm{2}}} +{e}^{{i}\frac{\pi}{\mathrm{4}}} −\mathrm{1}\right)\:=\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} \left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\mathrm{1}+{i}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\mathrm{3}\right)\right) \\ $$$${h}\:=\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} \left(\mathrm{3}{e}^{{i}\frac{\mathrm{11}\pi}{\mathrm{6}}} +{e}^{{i}\frac{\mathrm{11}\pi}{\mathrm{12}}} −\mathrm{1}\right) \\ $$$${h}\:=\:\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{6}}} \left(\mathrm{3}{e}^{{i}\frac{\mathrm{19}\pi}{\mathrm{6}}} +{e}^{{i}\frac{\mathrm{19}\pi}{\mathrm{12}}} −\mathrm{1}\right) \\ $$$$ \\ $$$$ \\ $$

Commented by MJS_new last updated on 19/Sep/20

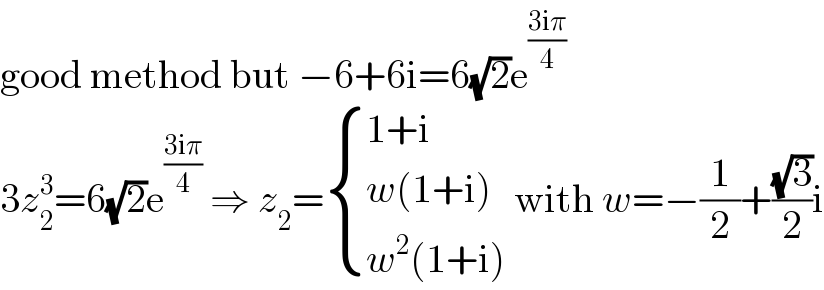
good method but −6+6i=6(√2)e^((3iπ)/4) 3z_2 ^3 =6(√2)e^((3iπ)/4) ⇒ z_2 = { ((1+i)),((w(1+i))),((w^2 (1+i))) :} with w=−(1/2)+((√3)/2)i

$$\mathrm{good}\:\mathrm{method}\:\mathrm{but}\:−\mathrm{6}+\mathrm{6i}=\mathrm{6}\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{3i}\pi}{\mathrm{4}}} \\ $$$$\mathrm{3}{z}_{\mathrm{2}} ^{\mathrm{3}} =\mathrm{6}\sqrt{\mathrm{2}}\mathrm{e}^{\frac{\mathrm{3i}\pi}{\mathrm{4}}} \:\Rightarrow\:{z}_{\mathrm{2}} =\begin{cases}{\mathrm{1}+\mathrm{i}}\\{{w}\left(\mathrm{1}+\mathrm{i}\right)}\\{{w}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{i}\right)}\end{cases}\:\mathrm{with}\:{w}=−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$

Commented by mohammad17 last updated on 19/Sep/20

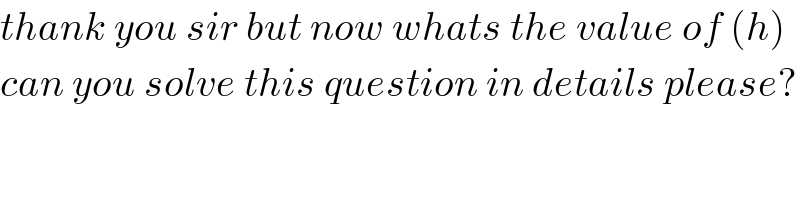
thank you sir but now whats the value of (h) can you solve this question in details please?

$${thank}\:{you}\:{sir}\:{but}\:{now}\:{whats}\:{the}\:{value}\:{of}\:\left({h}\right) \\ $$$${can}\:{you}\:{solve}\:{this}\:{question}\:{in}\:{details}\:{please}? \\ $$

Commented by MJS_new last updated on 19/Sep/20

z_1 =3z_2 ^2 = { ((6i)),((6w^2 i)),((6w^4 i=6wi)) :} z_1 +z_2 =h+1 ⇔ h=z_1 +z_2 −1= { ((7i)),((−((3−5(√3))/2)−((7−(√3))/2)i)),((−((3+5(√3))/2)−((7+(√3))/2)i)) :}

$${z}_{\mathrm{1}} =\mathrm{3}{z}_{\mathrm{2}} ^{\mathrm{2}} =\begin{cases}{\mathrm{6i}}\\{\mathrm{6}{w}^{\mathrm{2}} \mathrm{i}}\\{\mathrm{6}{w}^{\mathrm{4}} \mathrm{i}=\mathrm{6}{w}\mathrm{i}}\end{cases} \\ $$$${z}_{\mathrm{1}} +{z}_{\mathrm{2}} ={h}+\mathrm{1}\:\Leftrightarrow\:{h}={z}_{\mathrm{1}} +{z}_{\mathrm{2}} −\mathrm{1}=\begin{cases}{\mathrm{7i}}\\{−\frac{\mathrm{3}−\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{7}−\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}}\\{−\frac{\mathrm{3}+\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\mathrm{7}+\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i}}\end{cases} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com