
Question and Answers Forum
Question Number 114403 by bemath last updated on 19/Sep/20
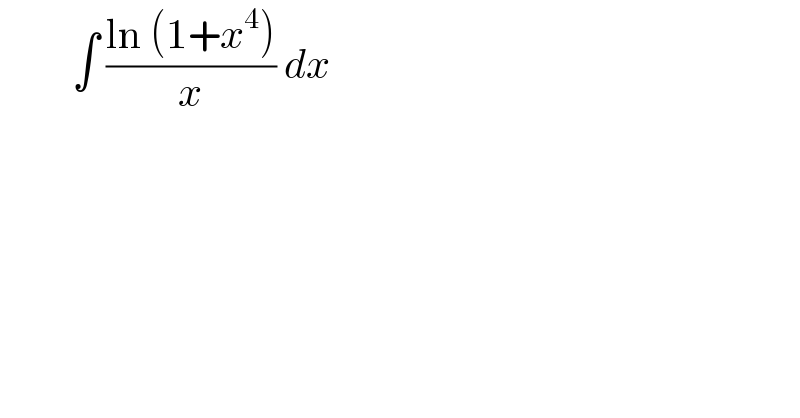
Commented by Dwaipayan Shikari last updated on 19/Sep/20
![∫_0 ^1 (−1)^n .Σ_(n=1) ^∞ (x^(4n−1) /n)dx Σ_(n=1) ^∞ (−1)^n ∫_0 ^1 (x^(4n−1) /n)dx Σ^∞ (−1)^n [(x^(4n) /(4n.n))]_0 ^1 (1/4)Σ^∞ (−1)^n (1/n^2 )=(π^2 /(48))](Q114492.png)
Answered by mathmax by abdo last updated on 19/Sep/20
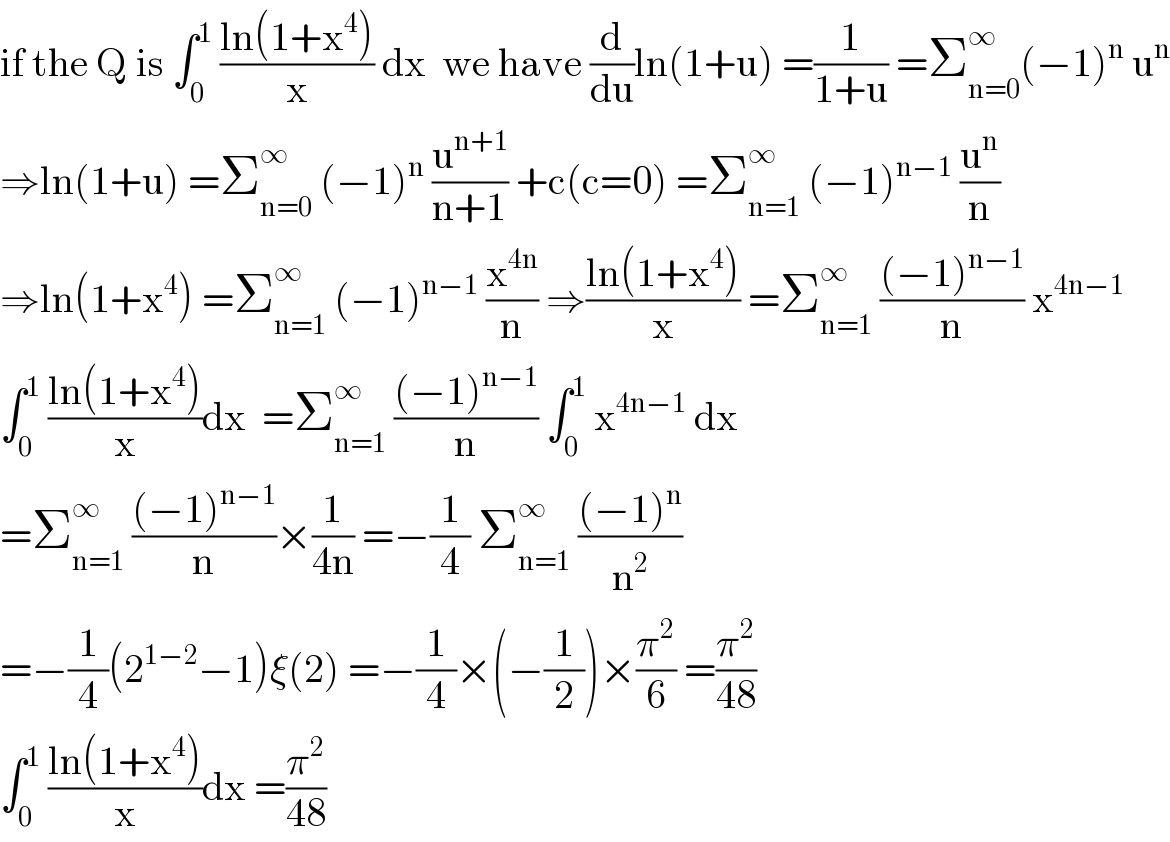
| ||
Question and Answers Forum | ||
Question Number 114403 by bemath last updated on 19/Sep/20 | ||
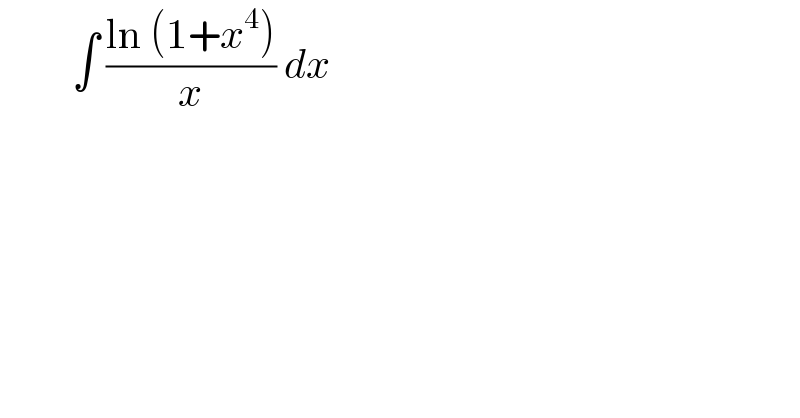 | ||
Commented by Dwaipayan Shikari last updated on 19/Sep/20 | ||
![∫_0 ^1 (−1)^n .Σ_(n=1) ^∞ (x^(4n−1) /n)dx Σ_(n=1) ^∞ (−1)^n ∫_0 ^1 (x^(4n−1) /n)dx Σ^∞ (−1)^n [(x^(4n) /(4n.n))]_0 ^1 (1/4)Σ^∞ (−1)^n (1/n^2 )=(π^2 /(48))](Q114492.png) | ||
Answered by mathmax by abdo last updated on 19/Sep/20 | ||
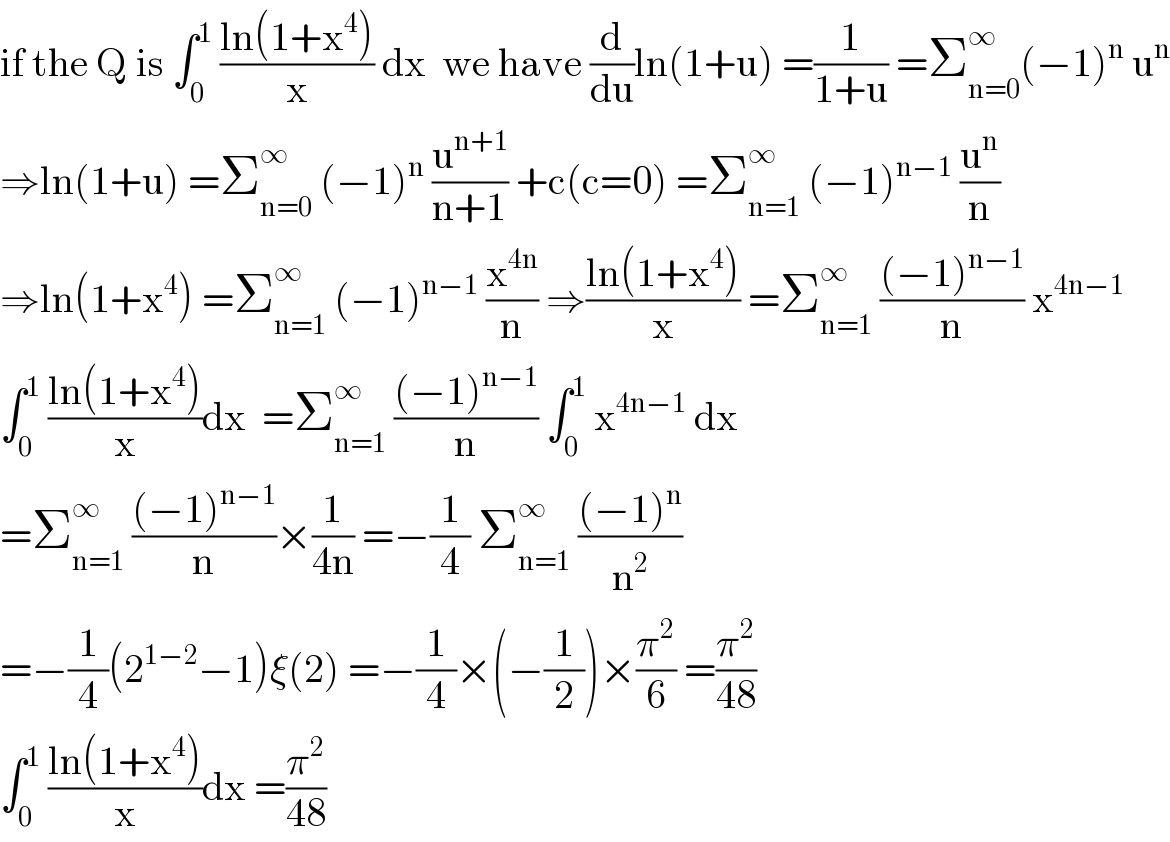 | ||
| ||