Question Number 114422 by Aina Samuel Temidayo last updated on 19/Sep/20

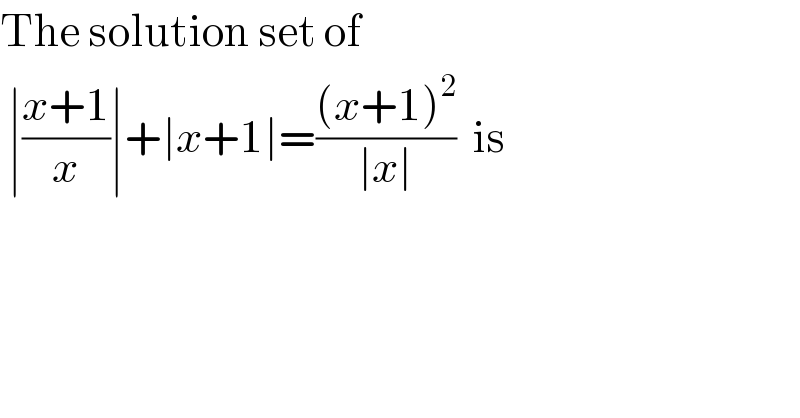
The solution set of ∣((x+1)/x)∣+∣x+1∣=(((x+1)^2 )/(∣x∣)) is

Commented bybemath last updated on 19/Sep/20

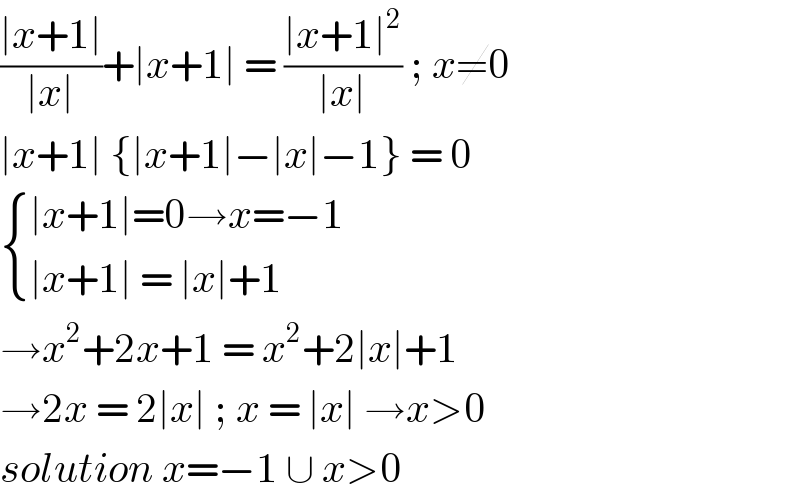
((∣x+1∣)/(∣x∣))+∣x+1∣ = ((∣x+1∣^2 )/(∣x∣)) ; x≠0 ∣x+1∣ {∣x+1∣−∣x∣−1} = 0 { ((∣x+1∣=0→x=−1)),((∣x+1∣ = ∣x∣+1)) :} →x^2 +2x+1 = x^2 +2∣x∣+1 →2x = 2∣x∣ ; x = ∣x∣ →x>0 solution x=−1 ∪ x>0

Commented byAina Samuel Temidayo last updated on 19/Sep/20

This is not its only solution.

Commented bybemath last updated on 19/Sep/20

it only solution

Answered by 1549442205PVT last updated on 19/Sep/20

Solve the eqution ∣((x+1)/x)∣+∣x+1∣=(((x+1)^2 )/(∣x∣)) (1) We need the condition x≠0 We have the following tablet: determinant ((x,,(−1),,0,),((∣((x+1)/x)∣),((x+1)/x),0,(−((x+1)/x)),(∣∣),((x+1)/x)),((∣x+1∣),(−x−1),0,(x+1),1,(x+1)),((((x+1)^2 )/(∣x∣)),(−(((x+1)^2 )/x)),0,(−(((x+1)^2 )/x)),(∣∣),(((x+1)^2 )/x))) From above tablet we get i)If x≤−1 then (1)⇔((x+1)/x)−x−1=−(((x+1)^2 )/x) ⇔(x+1)^2 −x(x+1)+x+1=0 ⇔x^2 +2x+1−x^2 −x+x+1=0 ⇔2x+2=0⇔x+1=0⇔x=−1 ii)If −1<x<0 then (1)⇔−((x+1)/x)+x+1=−(((x+1)^2 )/x) ⇔(x+1)^2 +x(x+1)−(x+1)=0 ⇔x^2 +2x+1+x^2 +x−x−1=0 ⇔2x^2 +2x=0⇔2x(x+1)=0 ⇔x+1=0 (rejected as don′t satisfy ii)) iii)If x>0 then (1)⇔((x+1)/x)+x+1=(((x+1)^2 )/x) ⇔(x+1)^2 −x(x+1)−(x+1)=0 ⇔x^2 +2x+1−x^2 −x−x−1=0 ⇔0.x=0⇒∀x>0 are roots Combining three above cases we get the roots of given equation are x∈{−1}∪(0;+∞)

Answered by Aina Samuel Temidayo last updated on 19/Sep/20

= ((∣x+1∣)/(∣x∣))+∣x+1∣ = (((x+1)^2 )/(∣x∣)), x≠0 CASE I: when x+1≥0 and x≥0 x≥−1 and x≥0 Finding their intersections ⇒ x≥0 but x≠0 ⇒ x>0 ⇒ ∣((x+1)/x)∣+∣x+1∣=(((x+1)^2 )/(∣x∣)) = ((x+1)/x)+x+1= ((x^2 +2x+1)/x) ⇒ x+1+x^2 +x= x^2 +2x+1 ⇒ 0=0 ⇒ x∈R Recall x>0 ⇒ x>0 CASE II: when x+1<0 and x<0 ⇒ x<−1 and x<0 ⇒ x<−1 ∣((x+1)/x)∣+∣x+1∣=(((x+1)^2 )/(∣x∣)) =((−(x+1))/(−(x)))+(−(x+1))= ((x^2 +2x+1)/(−(x))) ⇒−x−1+(−x(−(x+1)))=x^2 +2x+1 ⇒−x−1+(−x(−x−1))=x^2 +2x+1 ⇒−x−1+x^2 +x=x^2 +2x+1 ⇒x=−1 since x<−1 ⇒ x∈φ CASE III: when x+1<0 and x≥0 ⇒ x<−1 and x≥0 Finding their intersections ⇒ x∈φ CASE IV: when x+1≥0 and x<0 ⇒ x≥−1 and x<0 ⇒ x∈ [−1,0) ⇒∣((x+1)/x)∣+∣x+1∣=(((x+1)^2 )/(∣x∣)) ⇒((x+1)/(−x))+x+1=((x^2 +2x+1)/(−x)) ⇒(x+1)−x(x+1)=x^2 +2x+1 ⇒ x+1−x^2 −x=x^2 +2x+1 ⇒ 2x^2 +2x=0 ⇒x(x+1)=0 ⇒x=0 or x=−1 since x∈[−1,0) ⇒ x=−1 Combining Cases I,II,III and IV ⇒ x∈ (0,+∞) ∪ [−1] ⇒ x∈ {−1} ∪ (0,+∞)

Commented byruwedkabeh last updated on 19/Sep/20

Case II −(x+1)

Commented byAina Samuel Temidayo last updated on 19/Sep/20

What was my error please?

Commented byAina Samuel Temidayo last updated on 19/Sep/20

Corrected. Thanks.^

Answered by mnjuly1970 last updated on 19/Sep/20

solution::(x+1)^2 =∣x+1∣^2 ∣x+1∣((1/(∣x∣))+1−((∣x+1∣)/(∣x∣)))=0 x=−1 ✓ or (1/(∣x∣))+1−((∣x+1∣)/(∣x∣))=0 if x<−1 ⇒−(1/x)+1+[((x+1)/x)=1+(1/x)]=0 2=0 impossible if −1≤x≤0 ⇒ −(1/x)+1−1−(1/x)=0⇒((−2)/x)=0 again it is impossible. x>0⇒ (1/x)+1−1−(1/x)=0 ✓✓ ans {−1}∪ x>0 ✓