Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 114635 by mathmax by abdo last updated on 20/Sep/20

$$\mathrm{find}{\int }_0^1{\mathrm{x}}^4\ln \left(\mathrm{x}\right)\ln (1-{\mathrm{x}}^2)\mathrm{dx}$$

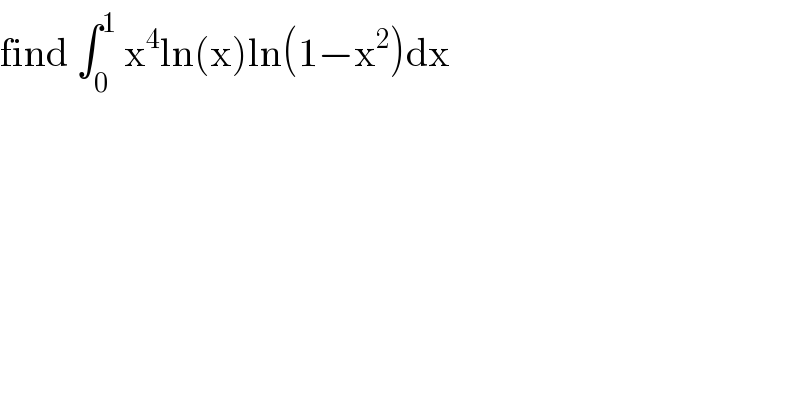
Commented by mathdave last updated on 20/Sep/20

Commented by mathdave last updated on 20/Sep/20

Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\mathrm{sir}$$

Answered by maths mind last updated on 20/Sep/20

$$ln(1-x^2)=-\sum _{k⩾0}\frac{x^{2k+2}}{k+1}$$$$={\int }_0^1\sum _{k⩾0}\frac{x^{2k+6}}{(k+1)}ln\left(x\right)dx$$$$=-\sum _{k⩾0}\frac{1}{k+1}{\int }_0^1{x}^{2k+6}ln\left(x\right)dx$$$$=\sum _{k⩾0}\frac{1}{(k+1){(2k+7)}^2}$$$$\mathrm{\Sigma }(\frac{1}{25(k+1)}-\frac{2}{5{(2k+7)}^2}+\frac{a}{(2k+7)})$$$$=\left(\frac{{(2k+7)}^2-10(k+1)+25a(k+1)(2k+7)}{25(k+1){(2k+7)}^2}\right)$$$$50a=-4\Rightarrow$$$$=\frac{1}{25}\sum _{k⩾0}(\frac{1}{k+1}-\frac{10}{{(2k+7)}^2}-\frac{2}{(2k+7)})$$$$=\frac{1}{25}\sum _{k⩾0}(\frac{1}{k+1}-\frac{2}{2k+7})-2\sum _{k⩾0}\frac{1}{{(2k+7)}^2}$$$$=\frac{1}{25}\mathrm{\Sigma }\left(\frac{2k+7-2k-2}{(2k+7)(k+1)}\right)-\frac{2}{25}\sum _{k⩾0}\frac{1}{{(2k+7)}^2}$$$$=\frac{1}{5}\sum _{k⩾0}\frac{1}{2(k+\frac{7}{2})(k+1)}-\frac{2}{25}\sum _{k⩾0}\frac{1}{{(2(k+3)+1)}^2}$$$$=\frac{1}{15}\sum _{k⩾0}\frac{\frac{7}{2}-1}{(k+\frac{7}{2})(k+1)}-\frac{2}{25}\sum _{k⩾3}\frac{1}{{(2k+1)}^2}$$$$=\frac{1}{15}(\mathrm{\Psi }\left(\frac{7}{2}\right)-\mathrm{\Psi }\left(1\right))-\frac{2}{25}(\left(\sum _{k⩾0}\frac{1}{{(2k+1)}^2}\right)-1-\frac{1}{9}-\frac{1}{25})$$$$\mathrm{\Psi }\left(\frac{7}{2}\right)=\mathrm{\Psi }\left(\frac{1}{2}\right)+\frac{2}{5}+\frac{2}{3}+2=\mathrm{\Psi }\left(\frac{1}{2}\right)+\frac{46}{15}$$$$\sum _{k⩾0}{\left(\frac{1}{2k+1}\right)}^2=\frac{3}{4}\zeta \left(2\right)=\frac{{\pi }^2}{8}$$$$\mathrm{\Psi }\left(\frac{1}{2}\right)=-\gamma -2ln\left(2\right)$$$$weget$$$$\frac{1}{15}(-\gamma -2ln\left(2\right)+\frac{46}{15}-(-\gamma ))-\frac{2}{25}(\frac{{\pi }^2}{48}-\frac{259}{225})$$$$$$$$$$$$$$$$$$

Commented by Tawa11 last updated on 06/Sep/21

$$\mathrm{great}\mathrm{sur}$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com