
Question and Answers Forum
Question Number 114699 by bemath last updated on 20/Sep/20
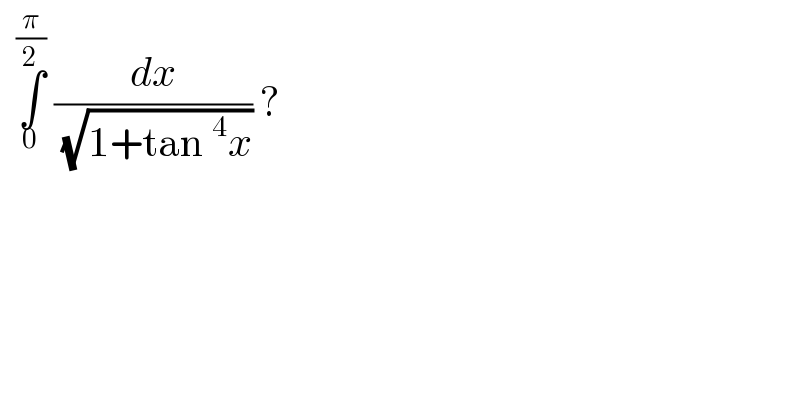
Commented by Dwaipayan Shikari last updated on 20/Sep/20

Answered by bobhans last updated on 20/Sep/20
![replacing x = (π/2)−x I=∫_(π/2) ^0 ((−dx)/( (√(1+tan^4 ((π/2)−x))))) I=∫_0 ^(π/2) (dx/( (√(1+cot^4 x)))) = ∫_0 ^(π/2) ((tan^2 x)/( (√(tan^4 x+1))))dx 2I=∫_0 ^(π/2) ((sec^2 x)/( (√(tan^4 x+1)))) dx I=(1/2)∫_1 ^∞ (dt/( (√(t^4 +1)))) ; [ t = tan x ] set q = 1+t^4 ; t = (q−1)^(1/4) I=(1/2)∫_1 ^∞ (1/( (√q))).(1/4)(q−1)^(−(3/4)) dq I=(1/8)∫_1 ^∞ q^(−(1/2)) (q−1)^(−(3/4)) dq I= (1/( 8))∫_1 ^∞ q^(−(5/4)) (1−q^(−1) )^(−(3/4)) dq I=(1/8).((Γ^2 ((1/4)))/(Γ((1/2)))) = (1/(8(√π))).Γ^2 ((1/4))](Q114702.png)
| ||
Question and Answers Forum | ||
Question Number 114699 by bemath last updated on 20/Sep/20 | ||
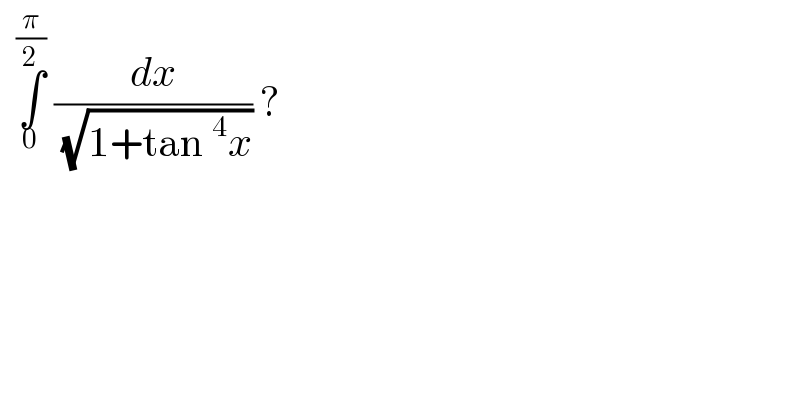 | ||
Commented by Dwaipayan Shikari last updated on 20/Sep/20 | ||
 | ||
Answered by bobhans last updated on 20/Sep/20 | ||
![replacing x = (π/2)−x I=∫_(π/2) ^0 ((−dx)/( (√(1+tan^4 ((π/2)−x))))) I=∫_0 ^(π/2) (dx/( (√(1+cot^4 x)))) = ∫_0 ^(π/2) ((tan^2 x)/( (√(tan^4 x+1))))dx 2I=∫_0 ^(π/2) ((sec^2 x)/( (√(tan^4 x+1)))) dx I=(1/2)∫_1 ^∞ (dt/( (√(t^4 +1)))) ; [ t = tan x ] set q = 1+t^4 ; t = (q−1)^(1/4) I=(1/2)∫_1 ^∞ (1/( (√q))).(1/4)(q−1)^(−(3/4)) dq I=(1/8)∫_1 ^∞ q^(−(1/2)) (q−1)^(−(3/4)) dq I= (1/( 8))∫_1 ^∞ q^(−(5/4)) (1−q^(−1) )^(−(3/4)) dq I=(1/8).((Γ^2 ((1/4)))/(Γ((1/2)))) = (1/(8(√π))).Γ^2 ((1/4))](Q114702.png) | ||
| ||