question proposed by m.n july 1970 show that ∫_0 ^∞ ((ln(1+x))/(x(1+x^2 )))dx=((5π^2 )/(48))


Question and Answers Forum

All Questions Topic List
None Questions
Previous in All Question Next in All Question
Previous in None Next in None
Question Number 114740 by mathdave last updated on 20/Sep/20

$q u e s t i o n p r o p o s e d b y m . n j u l y 1970$ $s h o w t h a t$ $\int_{0}^{\infty} \frac{\ln (1 + x)}{x (1 + x^{2})} d x = \frac{5 π^{2}}{48}$
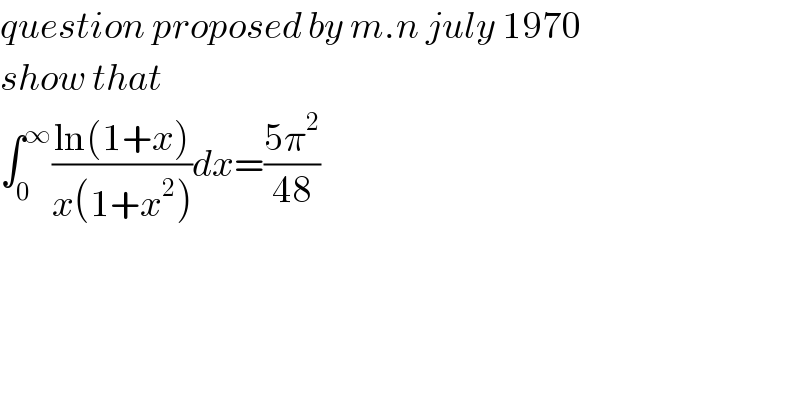
	Answered by mathdave last updated on 20/Sep/20

	$s o l u t i o n$ $l e t$ $I = \int_{0}^{\infty} \frac{\ln (1 + x)}{x (1 + x^{2})} d x = \int_{0}^{1} \frac{\ln (1 + x)}{x (1 + x^{2})} d x + \int_{1}^{\infty} \frac{\ln (1 + x)}{x (1 + x^{2})} d x$ $p u t x = \frac{1}{x} f o r t h e s e c o n d p a r t$ $I = \int_{0}^{1} \frac{\ln (1 + x)}{x (1 + x^{2})} d x + \int_{1}^{0} \frac{x \ln (1 + \frac{1}{x})}{(1 + \frac{1}{x^{2}})} \times - \frac{1}{x^{2}} d x$ $I = \int_{0}^{1} \frac{\ln (1 + x)}{x (1 + x^{2})} d x + \int_{0}^{1} \frac{x \ln (1 + x)}{(1 + x^{2})} d x - \int_{0}^{1} \frac{x \ln x}{(1 + x^{2})} d x$ $I = \int_{0}^{1} \frac{(1 + x^{2}) \ln (1 + x)}{x (1 + x^{2})} d x - {\int_{0}}^{1} \frac{x \ln x}{(1 + x^{2})} d x$ $I = \int_{0}^{1} \frac{\ln (1 + x)}{x} - \int_{0}^{1} \frac{x \ln x}{1 + x^{2}} d x = A - B$ $l e t A = \int_{0}^{1} \frac{\ln (1 + x)}{x} d x p u t x = - x$ $A = \int_{0}^{- 1} \frac{\ln (1 - x)}{x} d x = - {L i}_{2} (- 1) = - (- \frac{π^{2}}{12})$ $A = \frac{π^{2}}{12} . . . . . . . . . (1) t h e n$ $B = \int_{0}^{1} \frac{x \ln x}{1 + x^{2}} d x = {(- 1)}^{n} \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} x \ln x . x^{2 n} d x$ $B = {(- 1)}^{n} \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} x^{2 n + 1} \ln x d x$ $B = \frac{\partial}{\partial a} ∣_{a = 1} ({(- 1)}^{n} \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} x^{2 n + 1} . x^{a - 1} d x)$ $B = \frac{\partial}{\partial a} ∣_{a = 1} ({(- 1)}^{n} \underset{n = 0}{\sum^{\infty}} \int_{0}^{1} x^{2 n + a} d x) = \frac{\partial}{\partial a} ∣_{a = 1} ({(- 1)}^{n} \underset{n = 0}{\sum^{\infty}} (\frac{1}{2 n + a + 1}))$ $B = - \underset{n = 0}{\sum^{\infty}} \frac{{(- 1)}^{n}}{{(2 n + 2)}^{2}} = - \frac{1}{4} \underset{n = 0}{\sum^{\infty}} \frac{{(- 1)}^{n}}{{(n + 1)}^{2}}$ $B = - \frac{1}{4} \underset{n = 1}{\sum^{\infty}} \frac{{(- 1)}^{n - 1}}{n^{2}} = - \frac{1}{4} (\frac{π^{2}}{12}) = - \frac{π^{2}}{48}$ $b u t I = A - B = \frac{π^{2}}{12} - (- \frac{π^{2}}{12}) = \frac{5 π^{2}}{48}$ $∵ \int_{0}^{\infty} \frac{\ln (1 + x)}{x (1 + x^{2})} d x = \frac{5 π^{2}}{48}$ $b y m a t h d a v e (20 / 09 / 2020)$
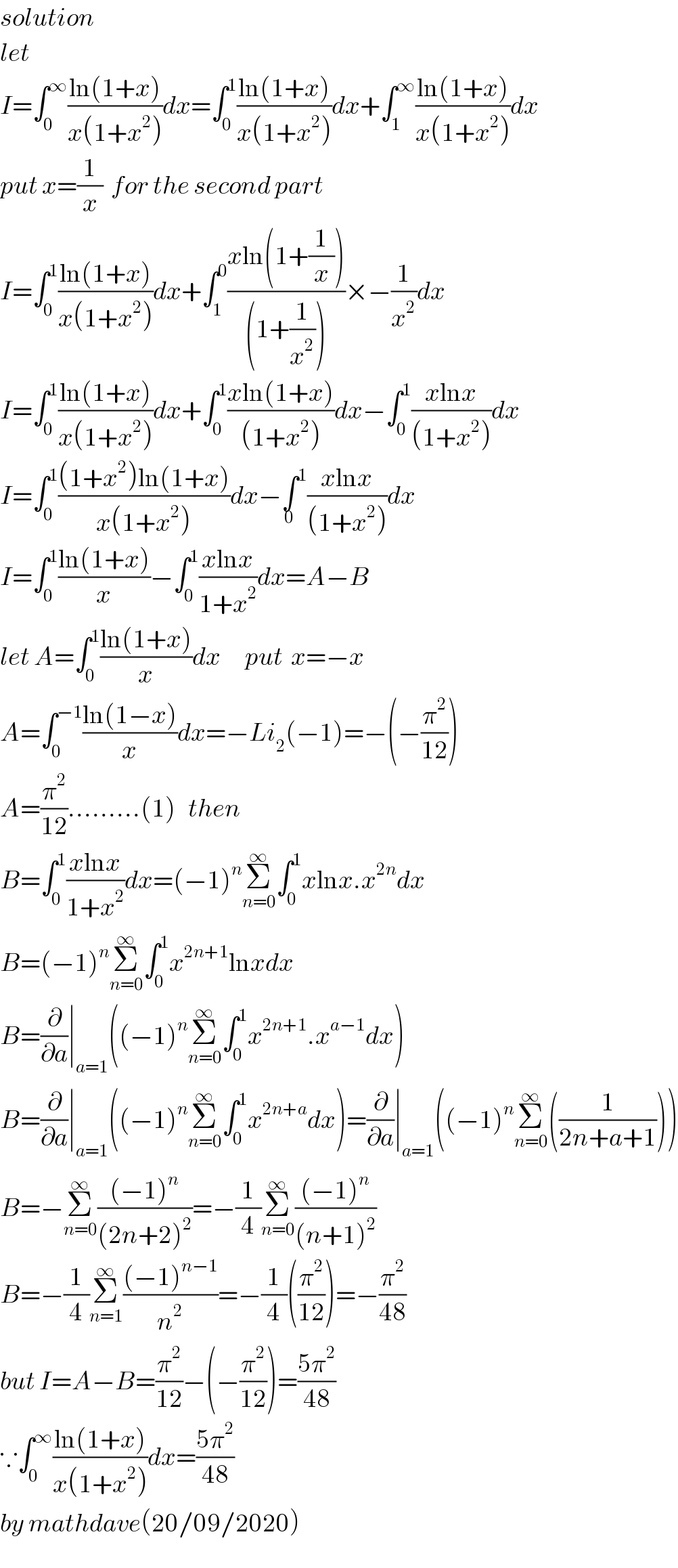
	Commented by mnjuly1970 last updated on 21/Sep/20

	$t h a n k y o u m r d a v e$
	Commented by Ar Brandon last updated on 21/Sep/20
	welldone ��
	Commented by Tawa11 last updated on 06/Sep/21

	$great sir$
	Answered by mathmax by abdo last updated on 20/Sep/20
	$I =∫_0 ^∞ ((ln(1+x))/(x(1+x^2 )))dx ⇒I =∫_0 ^1 ((ln(1+x))/(x(1+x^2 )))dx +∫_1 ^(+∞) ((ln(1+x))/(x(1+x^2 )))dx(→x=(1/t)) =∫_0 ^1 ((ln(1+x))/(x(1+x^2 )))dx +∫_0 ^1 t((ln(1+(1/t)))/((1+(1/t^2 ))))((dt/t^2 )) =∫_0 ^1 ((ln(1+x))/(x(1+x^2 )))dx +∫_0 ^1 ((x×(ln(1+x)−lnx))/(1+x^2 )) dt =∫_0 ^1 ((ln(1+x))/(x(1+x^2 )))dx +∫_0 ^1 ((x^2 ln(1+x))/(x(1+x^2 )))dx−∫_0 ^1 ((xln(x))/(1+x^2 ))dx =∫_0 ^1 ((ln(1+x))/x)dx−∫_0 ^1 ((xln(x))/(1+x^2 ))dx we have (d/dx)ln(1+x) =(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ln(1+x)=Σ_(n=0) ^∞ (((−1)^n x^(n+1) )/(n+1)) =Σ_(n=1) ^∞ (((−1)^(n−1) x^n )/n)⇒((ln(1+x))/x) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^(n−1) ⇒ ∫_0 ^1 ((ln(1+x))/x)dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−{2^(1−2) −1}ξ(2) =(π^2 /(12)) also we have ∫_0 ^1 ((xln(x))/(1+x^2 ))dx =∫_0 ^1 xlnxΣ_(n=0) ^∞ (−1)^n x^(2n) dx =Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(2n+1) ln(x)dx =Σ_(n=0) ^∞ (−1)^n u_n by parts u_n =[(x^(2n+2) /(2n+2))ln(x)]_0 ^1 −∫_0 ^1 (x^(2n+2) /(2n+2))(dx/x) =−(1/((2n+2)^2 )) ⇒ ∫_0 ^1 ((xlnx)/(1+x^2 ))dx =−Σ_(n=0) ^∞ (((−1)^n )/(4(n+1)^2 )) =−(1/4)Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =(1/4)Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =(1/4)(−(π^2 /(12))) =−(π^2 /(48)) ⇒ I =(π^2 /(12))+(π^2 /(48)) =((4π^2 +π^2 )/(48)) =((5π^2 )/(48))$
	$I = \int_{0}^{\infty} \frac{\ln (1 + x)}{x (1 + x^{2})} dx \Rightarrow I = \int_{0}^{1} \frac{\ln (1 + x)}{x (1 + x^{2})} dx + \int_{1}^{+ \infty} \frac{\ln (1 + x)}{x (1 + x^{2})} dx (\to x = \frac{1}{t})$ $= \int_{0}^{1} \frac{\ln (1 + x)}{x (1 + x^{2})} dx + \int_{0}^{1} t \frac{\ln (1 + \frac{1}{t})}{(1 + \frac{1}{t^{2}})} (\frac{dt}{t^{2}})$ $= \int_{0}^{1} \frac{\ln (1 + x)}{x (1 + x^{2})} dx + \int_{0}^{1} \frac{x \times (\ln (1 + x) - lnx)}{1 + x^{2}} dt$ $= \int_{0}^{1} \frac{\ln (1 + x)}{x (1 + x^{2})} dx + \int_{0}^{1} \frac{x^{2} \ln (1 + x)}{x (1 + x^{2})} dx - \int_{0}^{1} \frac{xln (x)}{1 + x^{2}} dx$ $= \int_{0}^{1} \frac{\ln (1 + x)}{x} dx - \int_{0}^{1} \frac{xln (x)}{1 + x^{2}} dx$ $we have \frac{d}{dx} \ln (1 + x) = \frac{1}{1 + x} = \sum_{n = 0}^{\infty} {(- 1)}^{n} x^{n} \Rightarrow \ln (1 + x) = \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n} x^{n + 1}}{n + 1}$ $= \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1} x^{n}}{n} \Rightarrow \frac{\ln (1 + x)}{x} = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n} x^{n - 1} \Rightarrow$ $\int_{0}^{1} \frac{\ln (1 + x)}{x} dx = \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n^{2}} = - \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n^{2}}$ $= - {2^{1 - 2} - 1} ξ (2) = \frac{π^{2}}{12} also we have$ $\int_{0}^{1} \frac{xln (x)}{1 + x^{2}} dx = \int_{0}^{1} xlnx \sum_{n = 0}^{\infty} {(- 1)}^{n} x^{2 n} dx$ $= \sum_{n = 0}^{\infty} {(- 1)}^{n} \int_{0}^{1} x^{2 n + 1} \ln (x) dx = \sum_{n = 0}^{\infty} {(- 1)}^{n} u_{n}$ $by parts u_{n} = {[\frac{x^{2 n + 2}}{2 n + 2} \ln (x)]}_{0}^{1} - \int_{0}^{1} \frac{x^{2 n + 2}}{2 n + 2} \frac{dx}{x} = - \frac{1}{{(2 n + 2)}^{2}} \Rightarrow$ $\int_{0}^{1} \frac{xlnx}{1 + x^{2}} dx = - \sum_{n = 0}^{\infty} \frac{{(- 1)}^{n}}{4 {(n + 1)}^{2}} = - \frac{1}{4} \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n - 1}}{n^{2}}$ $= \frac{1}{4} \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n}}{n^{2}} = \frac{1}{4} (- \frac{π^{2}}{12}) = - \frac{π^{2}}{48} \Rightarrow$ $I = \frac{π^{2}}{12} + \frac{π^{2}}{48} = \frac{4 π^{2} + π^{2}}{48} = \frac{5 π^{2}}{48}$
	Commented by mnjuly1970 last updated on 21/Sep/20

	$t h a n k y o u s o m u c h$
	Commented by mathmax by abdo last updated on 21/Sep/20

	$you are welcome$
Terms of Service
Privacy Policy
Contact: info@tinkutara.com

Question and Answers Forum