
Question and Answers Forum
Question Number 114808 by mnjuly1970 last updated on 21/Sep/20
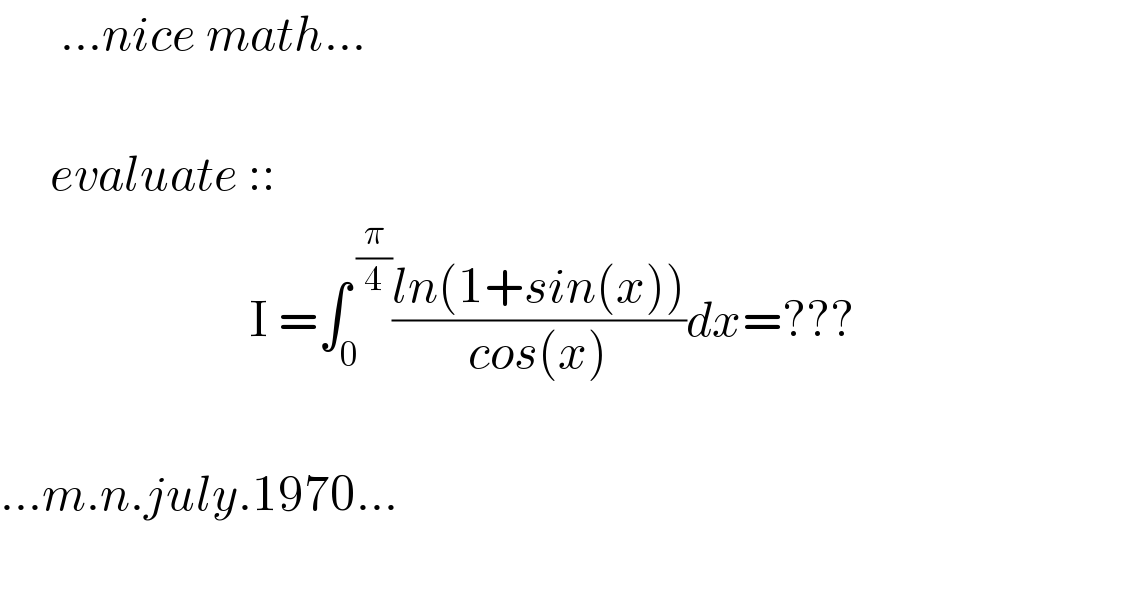
Answered by mathdave last updated on 22/Sep/20
![solution let I=∫_0 ^(π/4) ((ln(1+sinx))/(cosx))dx=∫_0 ^(π/4) ((ln(1+sinx))/(1−sin^2 x))cosxdx put y=sinx I=∫_0 ^(1/(√2)) ((ln(1+y))/(1−y^2 ))dy=(1/2)(∫_0 ^(1/(√2)) ((ln(1+y))/(1−y))dy+∫_0 ^(1/(√2)) ((ln(1+y))/(1+y))dy)=(1/2)(A+B) put y=1−2x in A let A=∫_((1/2)−((√2)/4)) ^(1/(√2)) ((ln(2−2x))/x)dx=∫_((1/2)−((√2)/4)) ^(1/2) (((ln(1−x))/x)+((ln2)/x))dx A=∫_((1/2)−((√2)/4)) ^(1/2) ((ln(1−x))/x)dx+ln2∫_((1/2)−((√2)/4)) ^(1/2) (1/x)dx A=[−Li_2 (x)]_((1/2)−((√2)/4)) ^(1/2) +ln2[lnx]_((1/2)−((√2)/4)) ^(1/2) A=−Li_2 ((1/2))+Li_2 ((1/2)−((√2)/4))+ln2[ln((1/2))−ln((1/2)−((√2)/4))] A=−ln^2 (2)−Li_2 ((1/2))+Li_2 ((1/2)−((√2)/4))−ln2ln(2−(√2))+2ln^2 (2) A=(3/2)ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln2ln(2−(√2)).....(1) and B=∫_0 ^(1/(√2)) ((ln(1+y))/(1+y))dy using IBP B=ln^2 (1+y)∣_0 ^(1/(√2)) −∫_0 ^(1/(√2)) ((ln(1+y))/(1+y))dy B=(1/2)ln^2 (1+(1/(√2)))=(1/2)ln^2 (((2+(√2))/2))=(1/2)[ln(((2+(√2))/2))]^2 B=(1/2)[ln(2+(√2))−ln2]^2 B=(1/2)ln^2 (2+(√2))+(1/2)ln^2 (2)−ln2ln(2+(√2))....(2) but I=(1/2)(A+B) I=(1/2)((3/2)ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln2ln(2−(√2))+(1/2)ln^2 (2+(√2))−ln2ln(2+(√2))+(1/2)ln^2 (2)) I=(1/2)(2ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln2[ln(2−(√2))+ln(2+(√2))]+(1/2)ln^2 (2+(√2))) I=(1/2)(2ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln^2 (2)+(1/2)ln^2 (2+(√2))) I=(1/2)Li_2 ((1/2)−((√2)/4))−(π^2 /(24))+(1/4)ln^2 (2+(√2))+(1/2)ln^2 (2) ∵∫_0 ^(π/4) ((ln(1+sinx))/(cosx))dx=(1/2)Li_2 ((1/2)−((√2)/4))−(π^2 /(24))+(1/4)ln^2 (2+(√2))+(1/2)ln^2 (2) by mathdave(22/09/2020)](Q114929.png)
Commented by mnjuly1970 last updated on 22/Sep/20
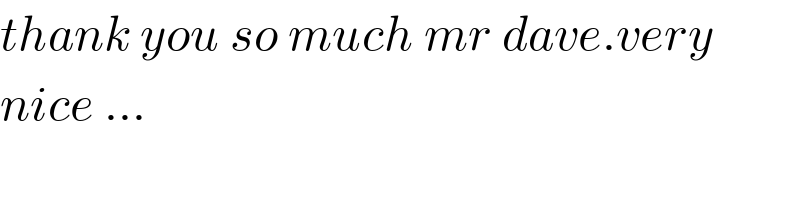
Commented by Tawa11 last updated on 06/Sep/21

| ||
Question and Answers Forum | ||
Question Number 114808 by mnjuly1970 last updated on 21/Sep/20 | ||
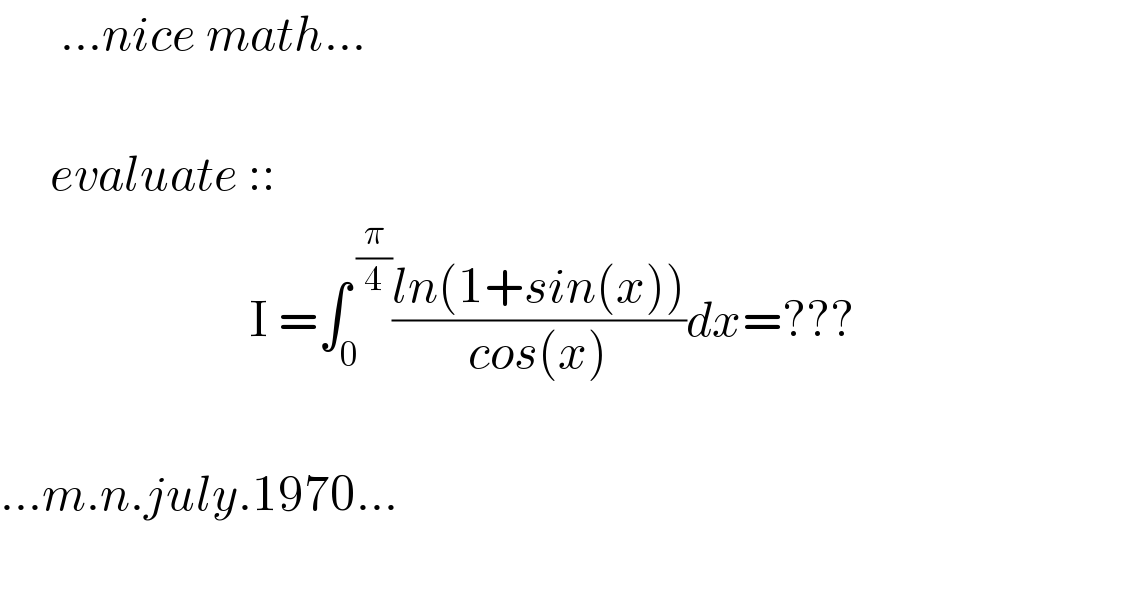 | ||
Answered by mathdave last updated on 22/Sep/20 | ||
![solution let I=∫_0 ^(π/4) ((ln(1+sinx))/(cosx))dx=∫_0 ^(π/4) ((ln(1+sinx))/(1−sin^2 x))cosxdx put y=sinx I=∫_0 ^(1/(√2)) ((ln(1+y))/(1−y^2 ))dy=(1/2)(∫_0 ^(1/(√2)) ((ln(1+y))/(1−y))dy+∫_0 ^(1/(√2)) ((ln(1+y))/(1+y))dy)=(1/2)(A+B) put y=1−2x in A let A=∫_((1/2)−((√2)/4)) ^(1/(√2)) ((ln(2−2x))/x)dx=∫_((1/2)−((√2)/4)) ^(1/2) (((ln(1−x))/x)+((ln2)/x))dx A=∫_((1/2)−((√2)/4)) ^(1/2) ((ln(1−x))/x)dx+ln2∫_((1/2)−((√2)/4)) ^(1/2) (1/x)dx A=[−Li_2 (x)]_((1/2)−((√2)/4)) ^(1/2) +ln2[lnx]_((1/2)−((√2)/4)) ^(1/2) A=−Li_2 ((1/2))+Li_2 ((1/2)−((√2)/4))+ln2[ln((1/2))−ln((1/2)−((√2)/4))] A=−ln^2 (2)−Li_2 ((1/2))+Li_2 ((1/2)−((√2)/4))−ln2ln(2−(√2))+2ln^2 (2) A=(3/2)ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln2ln(2−(√2)).....(1) and B=∫_0 ^(1/(√2)) ((ln(1+y))/(1+y))dy using IBP B=ln^2 (1+y)∣_0 ^(1/(√2)) −∫_0 ^(1/(√2)) ((ln(1+y))/(1+y))dy B=(1/2)ln^2 (1+(1/(√2)))=(1/2)ln^2 (((2+(√2))/2))=(1/2)[ln(((2+(√2))/2))]^2 B=(1/2)[ln(2+(√2))−ln2]^2 B=(1/2)ln^2 (2+(√2))+(1/2)ln^2 (2)−ln2ln(2+(√2))....(2) but I=(1/2)(A+B) I=(1/2)((3/2)ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln2ln(2−(√2))+(1/2)ln^2 (2+(√2))−ln2ln(2+(√2))+(1/2)ln^2 (2)) I=(1/2)(2ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln2[ln(2−(√2))+ln(2+(√2))]+(1/2)ln^2 (2+(√2))) I=(1/2)(2ln^2 (2)−(π^2 /(12))+Li_2 ((1/2)−((√2)/4))−ln^2 (2)+(1/2)ln^2 (2+(√2))) I=(1/2)Li_2 ((1/2)−((√2)/4))−(π^2 /(24))+(1/4)ln^2 (2+(√2))+(1/2)ln^2 (2) ∵∫_0 ^(π/4) ((ln(1+sinx))/(cosx))dx=(1/2)Li_2 ((1/2)−((√2)/4))−(π^2 /(24))+(1/4)ln^2 (2+(√2))+(1/2)ln^2 (2) by mathdave(22/09/2020)](Q114929.png) | ||
| ||
Commented by mnjuly1970 last updated on 22/Sep/20 | ||
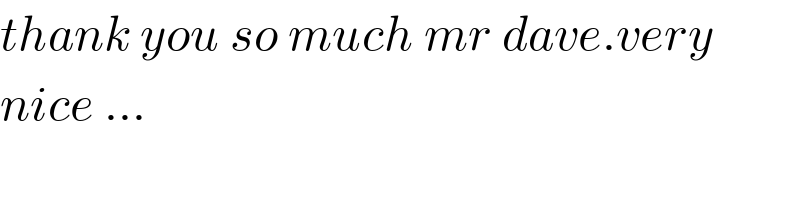 | ||
Commented by Tawa11 last updated on 06/Sep/21 | ||
 | ||