
Question and Answers Forum
Question Number 114922 by bemath last updated on 22/Sep/20
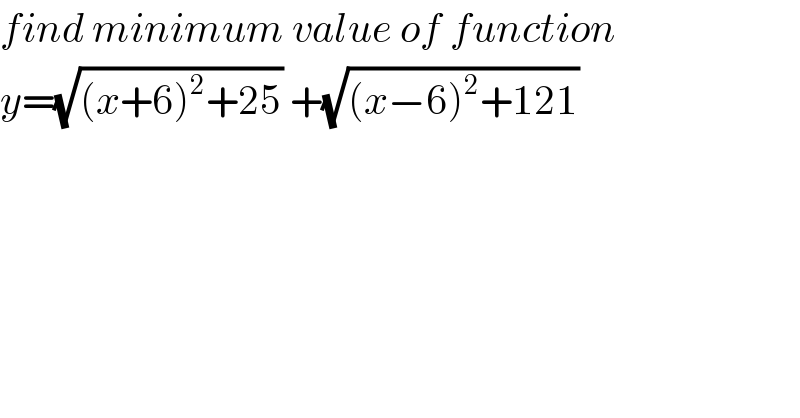
Answered by john santu last updated on 22/Sep/20

Commented by bemath last updated on 22/Sep/20

Answered by bobhans last updated on 22/Sep/20
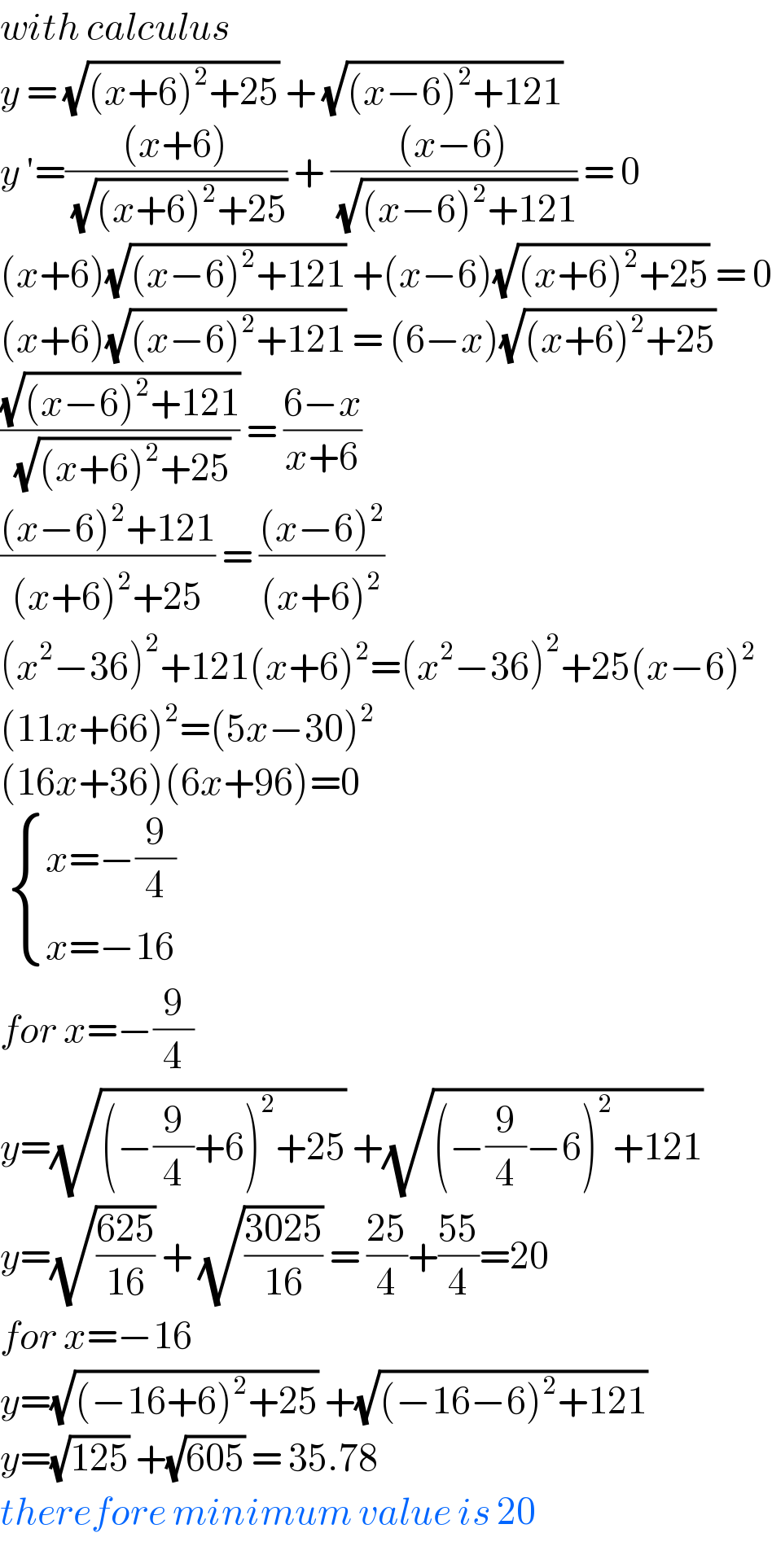
| ||
Question and Answers Forum | ||
Question Number 114922 by bemath last updated on 22/Sep/20 | ||
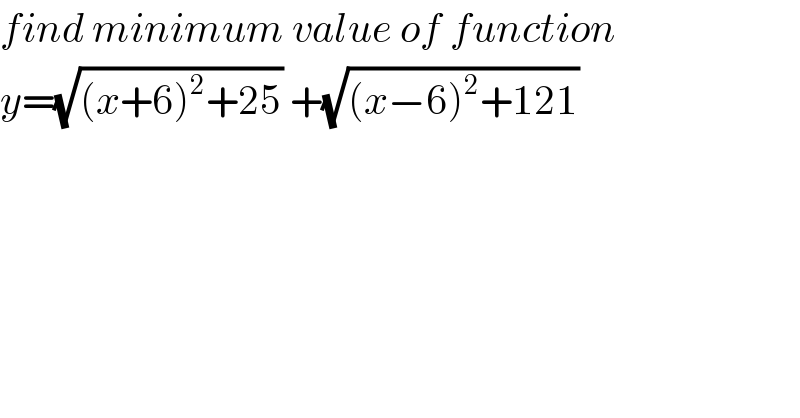 | ||
Answered by john santu last updated on 22/Sep/20 | ||
 | ||
| ||
Commented by bemath last updated on 22/Sep/20 | ||
 | ||
Answered by bobhans last updated on 22/Sep/20 | ||
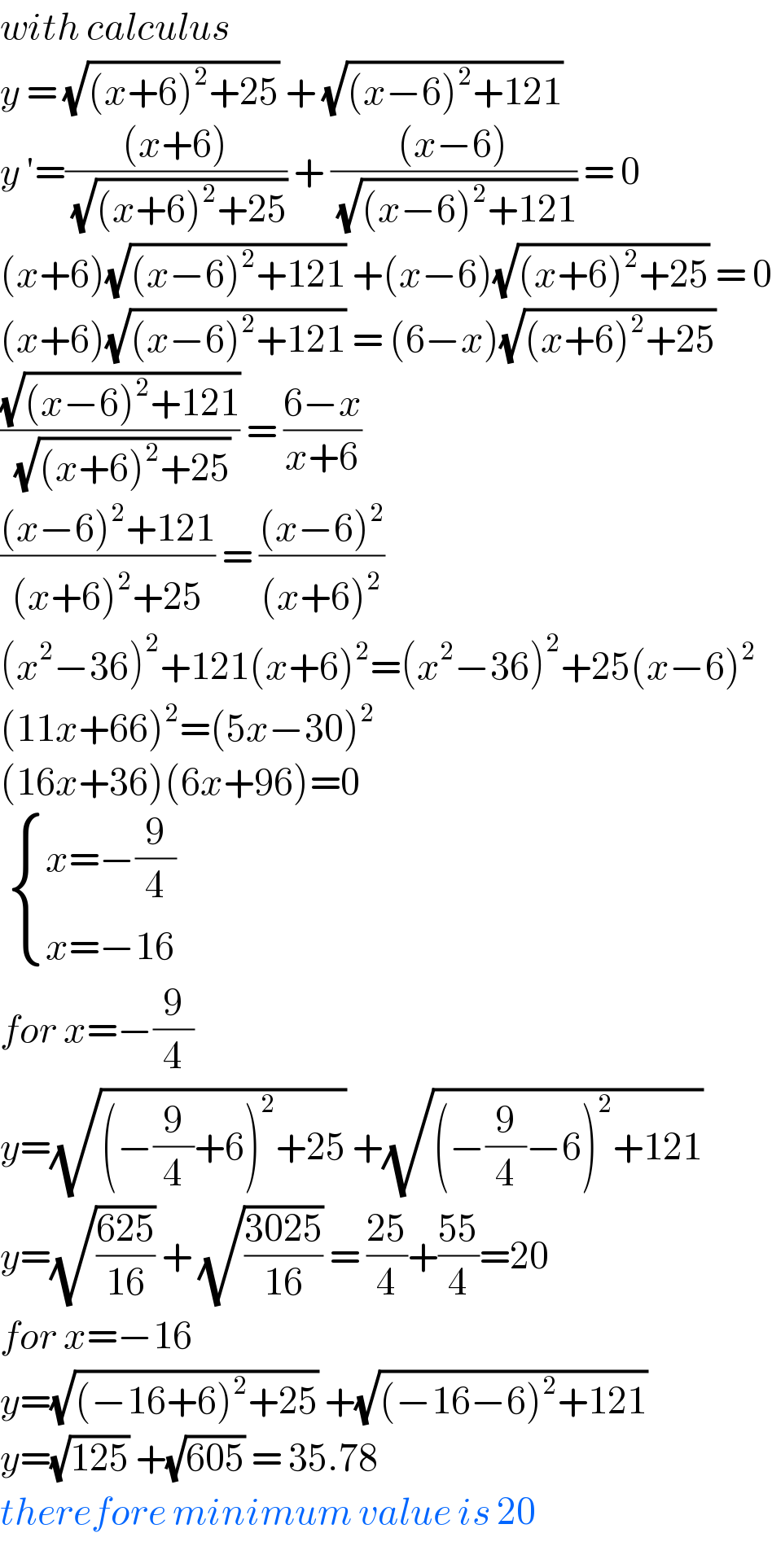 | ||
| ||