
Question and Answers Forum
Question Number 114996 by mnjuly1970 last updated on 22/Sep/20
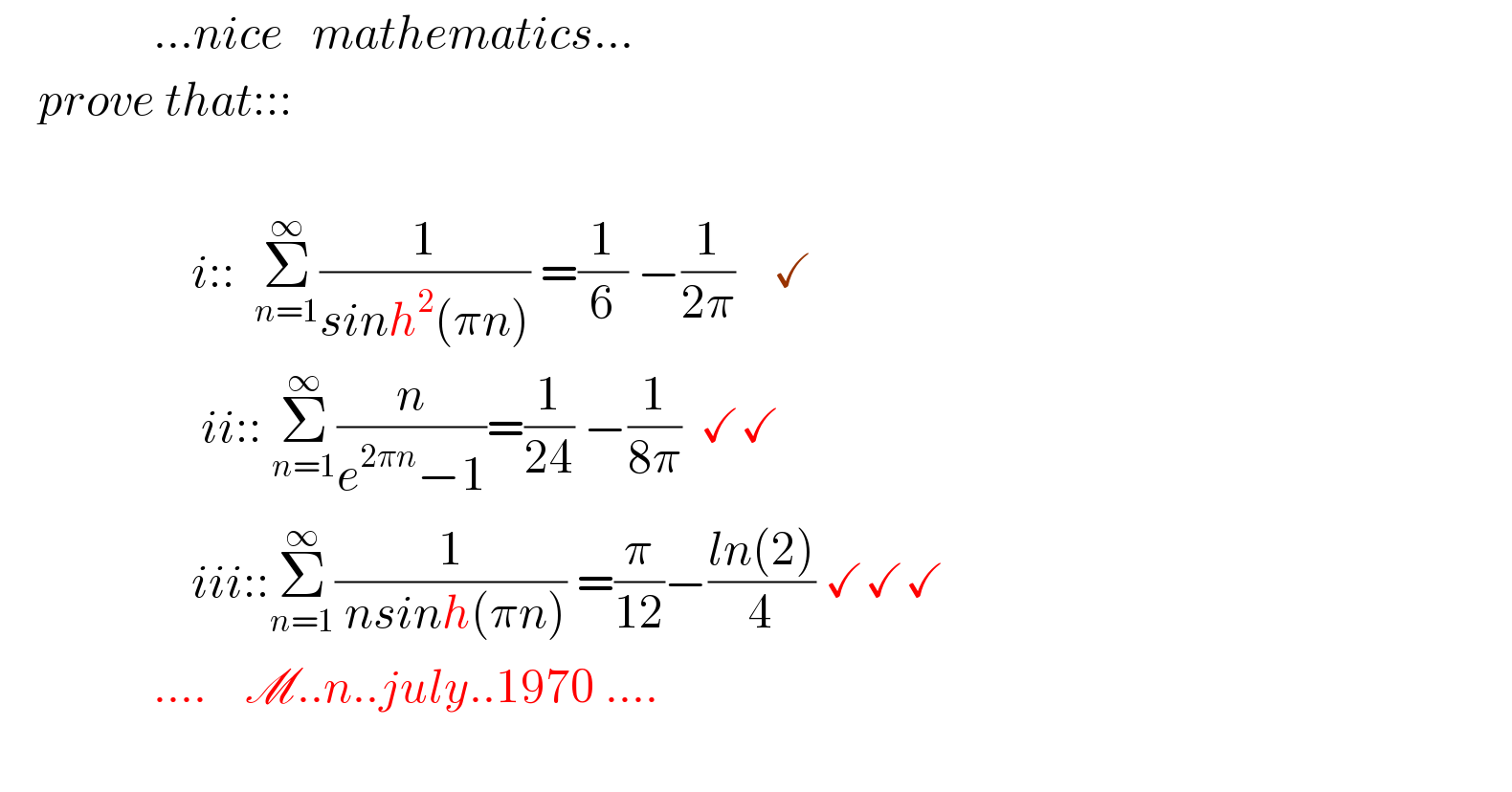
Commented by maths mind last updated on 24/Sep/20
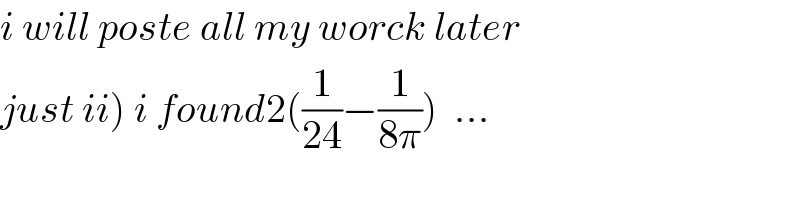
Answered by Olaf last updated on 23/Sep/20
![i:: I_n = ∫_n ^(n+1) (dx/(sinh^2 (πx))) I_n = ∫_n ^(n+1) (coth^2 (πx)−1)dx I_n = [(−(1/π)coth(πx)]_n ^(n+1) = (1/π)[coth(πn)−coth(π(n+1))] I_n = (1/π)[((cosh(πn))/(sinh(πn)))−((cosh(π(n+1)))/(sinh(π(n+1))))] I_n =(1/π) ((sinh(π(n+1))cosh(πn)−cosh(π(n+1)+cosh(πn))/(sinh(πn)sinh(π(n+1)))) I_n = (1/π)[((sinh(π(n+1)−πn])/(sinh(πn)sinh(π(n+1))))] I_n = (1/π)[((sinh(π))/(sinh(πn)sinh(π(n+1))))] (π/(sinh(π)))I_n = (1/(sinh(πn)sinh(π(n+1)))) (π/(sinh(π)))I_(n+1) ≤ (1/(sinh^2 (π(n+1)))) ≤ (π/(sinh(π)))I_n (π/(sinh(π)))Σ_(n=1) ^∞ I_(n+1) ≤ Σ_(n=1) ^∞ (1/(sinh^2 (π(n+1)))) ≤Σ_(n=1) ^∞ (π/(sinh(π)))I_n (π/(sinh(π)))Σ_(n=2) ^∞ I_n ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn)))−(1/(sinh^2 (π))) ≤Σ_(n=1) ^∞ (π/(sinh(π)))I_n (π/(sinh(π)))[−(1/π)coth(πx)]_2 ^∞ ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn)))−(1/(sinh^2 (π))) ≤ (π/(sinh(π)))[−(1/π)coth(πx)]_1 ^∞ (1/(sinh(π)))[coth(2π)−1] ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn)))−(1/(sinh^2 (π))) ≤ (1/(sinh(π)))[coth(π)−1] (1/(sinh(π)))[coth(2π)−1+(1/(sinh(π)))] ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn))) ≤ (1/(sinh(π)))[coth(π)−1+(1/(sinh(π)))]_1 ^∞ ((coth(2π)sinh(π)−sinh(π)+1)/(sinh^2 (π))) ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn))) ≤ [((cosh(π)−sinh(π)+1)/(sinh^2 (π)))] I tried but may be it is not the good way.](Q115160.png)
Answered by maths mind last updated on 24/Sep/20

| ||
Question and Answers Forum | ||
Question Number 114996 by mnjuly1970 last updated on 22/Sep/20 | ||
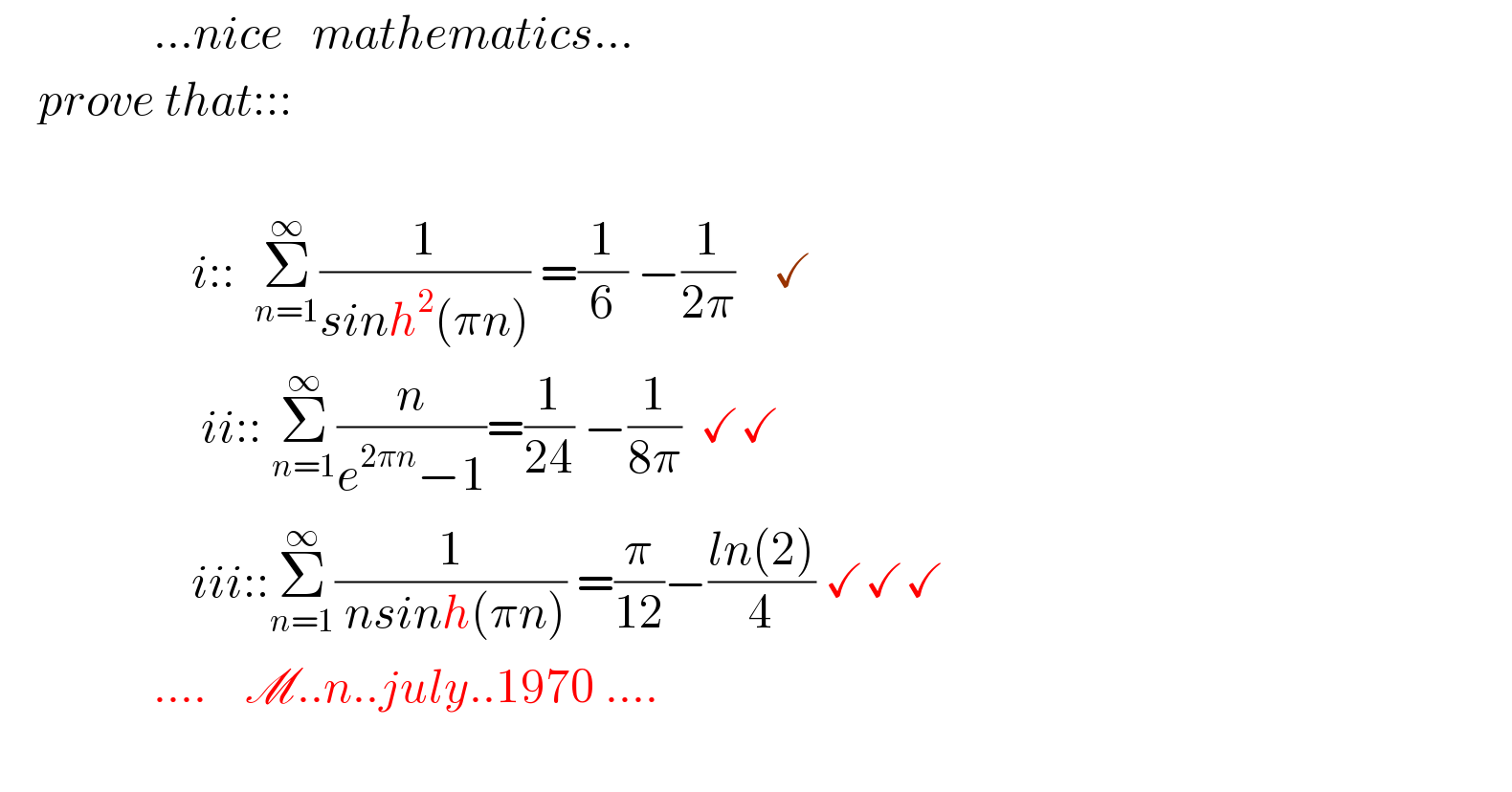 | ||
Commented by maths mind last updated on 24/Sep/20 | ||
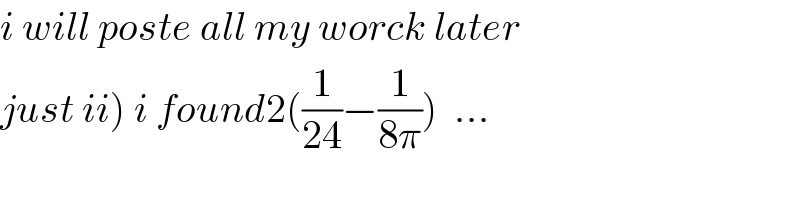 | ||
Answered by Olaf last updated on 23/Sep/20 | ||
![i:: I_n = ∫_n ^(n+1) (dx/(sinh^2 (πx))) I_n = ∫_n ^(n+1) (coth^2 (πx)−1)dx I_n = [(−(1/π)coth(πx)]_n ^(n+1) = (1/π)[coth(πn)−coth(π(n+1))] I_n = (1/π)[((cosh(πn))/(sinh(πn)))−((cosh(π(n+1)))/(sinh(π(n+1))))] I_n =(1/π) ((sinh(π(n+1))cosh(πn)−cosh(π(n+1)+cosh(πn))/(sinh(πn)sinh(π(n+1)))) I_n = (1/π)[((sinh(π(n+1)−πn])/(sinh(πn)sinh(π(n+1))))] I_n = (1/π)[((sinh(π))/(sinh(πn)sinh(π(n+1))))] (π/(sinh(π)))I_n = (1/(sinh(πn)sinh(π(n+1)))) (π/(sinh(π)))I_(n+1) ≤ (1/(sinh^2 (π(n+1)))) ≤ (π/(sinh(π)))I_n (π/(sinh(π)))Σ_(n=1) ^∞ I_(n+1) ≤ Σ_(n=1) ^∞ (1/(sinh^2 (π(n+1)))) ≤Σ_(n=1) ^∞ (π/(sinh(π)))I_n (π/(sinh(π)))Σ_(n=2) ^∞ I_n ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn)))−(1/(sinh^2 (π))) ≤Σ_(n=1) ^∞ (π/(sinh(π)))I_n (π/(sinh(π)))[−(1/π)coth(πx)]_2 ^∞ ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn)))−(1/(sinh^2 (π))) ≤ (π/(sinh(π)))[−(1/π)coth(πx)]_1 ^∞ (1/(sinh(π)))[coth(2π)−1] ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn)))−(1/(sinh^2 (π))) ≤ (1/(sinh(π)))[coth(π)−1] (1/(sinh(π)))[coth(2π)−1+(1/(sinh(π)))] ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn))) ≤ (1/(sinh(π)))[coth(π)−1+(1/(sinh(π)))]_1 ^∞ ((coth(2π)sinh(π)−sinh(π)+1)/(sinh^2 (π))) ≤ Σ_(n=1) ^∞ (1/(sinh^2 (πn))) ≤ [((cosh(π)−sinh(π)+1)/(sinh^2 (π)))] I tried but may be it is not the good way.](Q115160.png) | ||
| ||
Answered by maths mind last updated on 24/Sep/20 | ||
 | ||
| ||