
Question and Answers Forum
Question Number 115009 by arcana last updated on 22/Sep/20
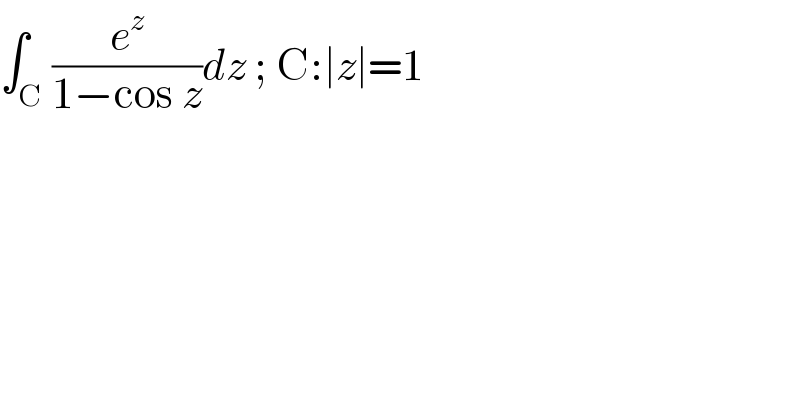
Answered by Olaf last updated on 24/Sep/20
![∫_C ((coz+isinz)/(1−cosz))dz ∫_C ((1+isinz+(cosz−1))/(1−cosz))dz ∫_C (dz/(1−cosz))+i∫_C ((sinz)/(1−cosz))−∫_C dz ∫_C ((2dz)/(sin^2 (z/2)))+i∫_C ((sinz)/(1−cosz))−∫_C dz [−4cot(z/2)+iln(1−cosz)−z]_C Let z = e^(iθ) , θ∈[0 ; 2π] [−4cot(e^(iθ) /2)+iln(1−cose^(iθ) )−e^(iθ) ]_0 ^(2π) = 0](Q115017.png)
Answered by Bird last updated on 24/Sep/20
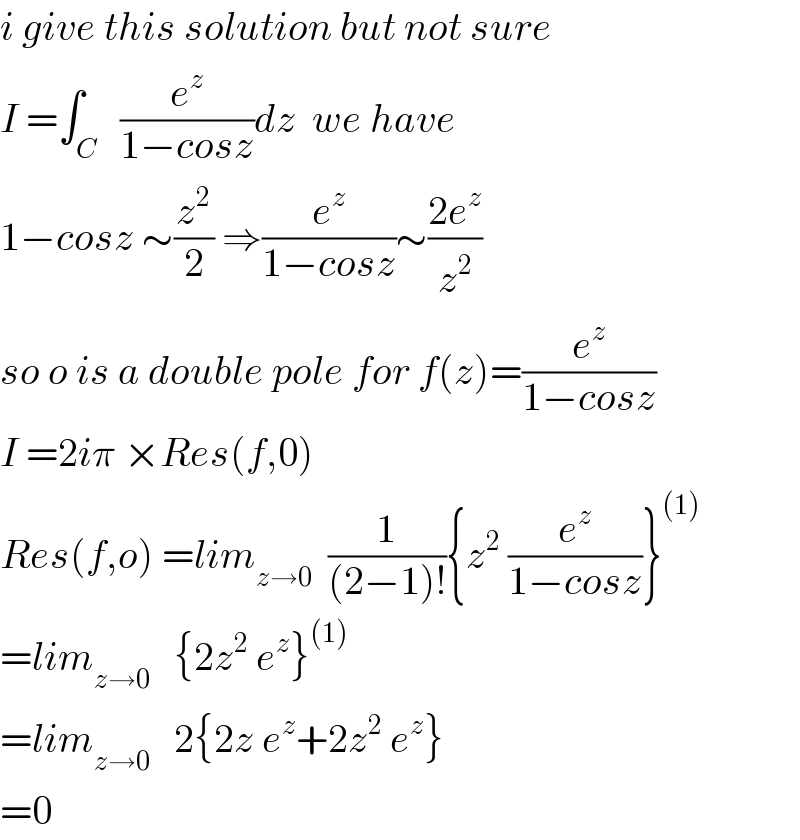
| ||
Question and Answers Forum | ||
Question Number 115009 by arcana last updated on 22/Sep/20 | ||
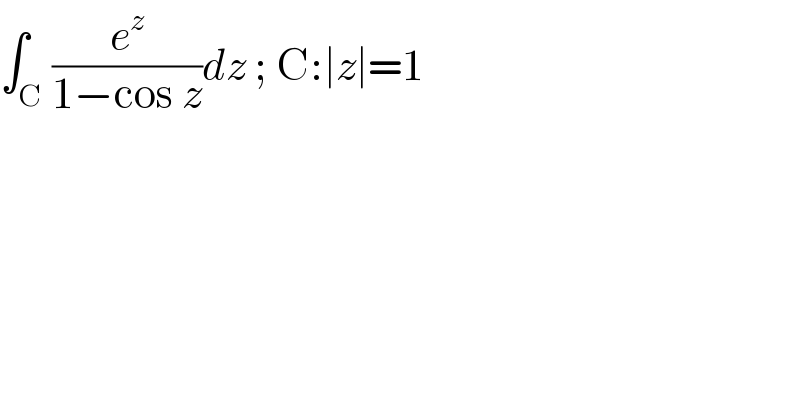 | ||
Answered by Olaf last updated on 24/Sep/20 | ||
![∫_C ((coz+isinz)/(1−cosz))dz ∫_C ((1+isinz+(cosz−1))/(1−cosz))dz ∫_C (dz/(1−cosz))+i∫_C ((sinz)/(1−cosz))−∫_C dz ∫_C ((2dz)/(sin^2 (z/2)))+i∫_C ((sinz)/(1−cosz))−∫_C dz [−4cot(z/2)+iln(1−cosz)−z]_C Let z = e^(iθ) , θ∈[0 ; 2π] [−4cot(e^(iθ) /2)+iln(1−cose^(iθ) )−e^(iθ) ]_0 ^(2π) = 0](Q115017.png) | ||
| ||
Answered by Bird last updated on 24/Sep/20 | ||
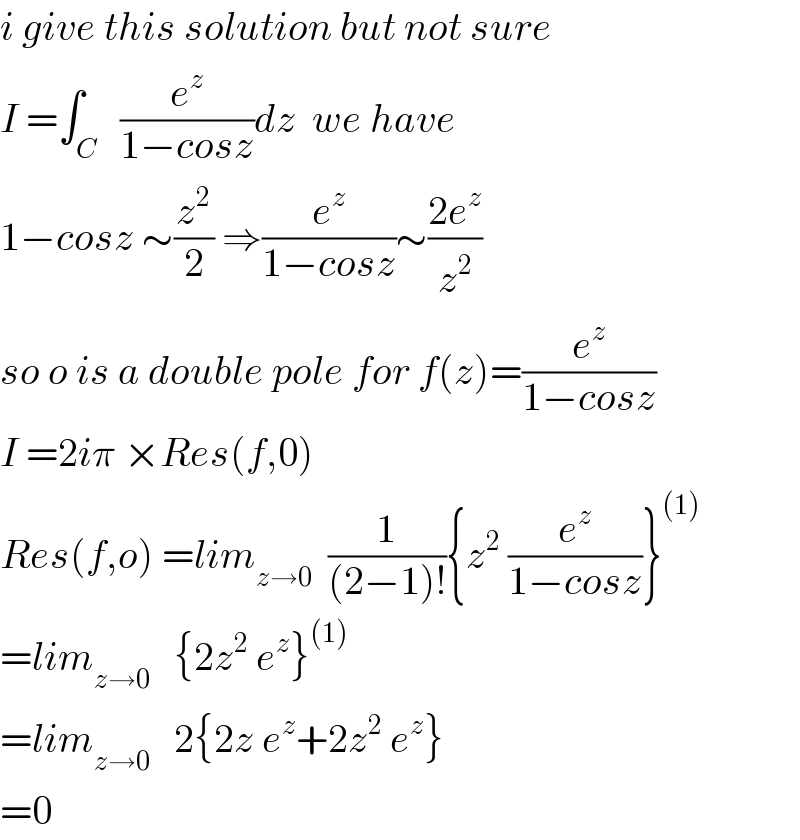 | ||
| ||