
Question and Answers Forum
Question Number 115014 by mathdave last updated on 23/Sep/20
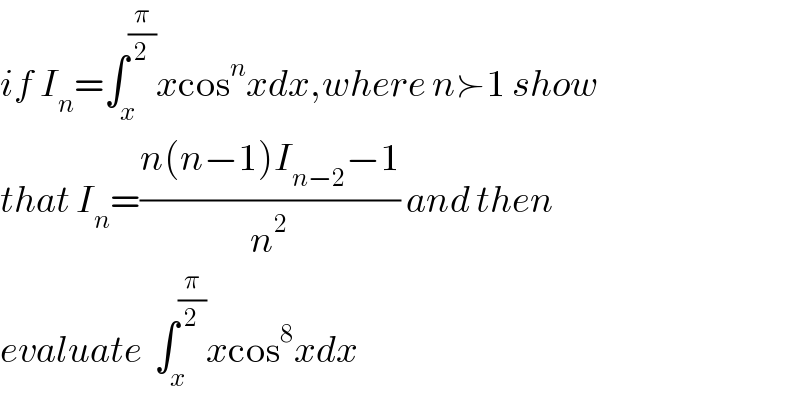
Answered by Olaf last updated on 23/Sep/20
![I_n = ∫_0 ^(π/2) xcos^n xdx I_n −I_(n+2) = ∫_0 ^(π/2) xcos^n x(1−cos^2 x)dx I_n −I_(n+2) = −∫_0 ^(π/2) (xsinx)(−sinxcos^n x)dx I_n −I_(n+2) = −[xsinx((cos^(n+1) x)/(n+1))]_0 ^(π/2) +∫_0 ^(π/2) (sinx+xcosx)((cos^(n+1) x)/(n+1))dx I_n −I_(n+2) = −∫_0 ^(π/2) (−sinx((cos^(n+1) x)/(n+1)))dx +(1/(n+1))I_(n+2) I_n −I_(n+2) = −[((cos^(n+2) x)/((n+1)(n+2)))]_0 ^(π/2) +(1/(n+1))I_(n+2) I_n = (1/((n+1)(n+2)))+I_(n+2) +(1/(n+1))I_(n+2) I_n = ((n+2)/(n+1))I_(n+2) +(1/((n+1)(n+2))) I_(n+2) = ((n+1)/(n+2))I_n −(1/((n+2)^2 )) (1) I_n = ((n(n−1)I_(n−2) −1)/n^2 ) I_0 = ∫_0 ^(π/2) xdx = [(x^2 /2)]_0 ^(π/2) = (π^2 /8) With (1) : I_2 = (1/2)((π^2 /8))−(1/4) = (π^2 /(16))−(1/4) I_4 = (3/4)((π^2 /(16))−(1/4))−(1/(16)) = ((3π^2 )/(64))−(1/4) I_6 = (5/6)(((3π^2 )/(64))−(1/4))−(1/(36)) = ((5π^2 )/(128))−((17)/(72)) I_8 = (7/8)(((5π^2 )/(128))−((17)/(72)))−(1/(64)) = ((35π^2 )/(1024))−(2/9) I_8 = ∫_0 ^(π/2) xcos^8 xdx = ((35π^2 )/(1024))−(2/9)](Q115155.png)
Commented by Tawa11 last updated on 06/Sep/21

| ||
Question and Answers Forum | ||
Question Number 115014 by mathdave last updated on 23/Sep/20 | ||
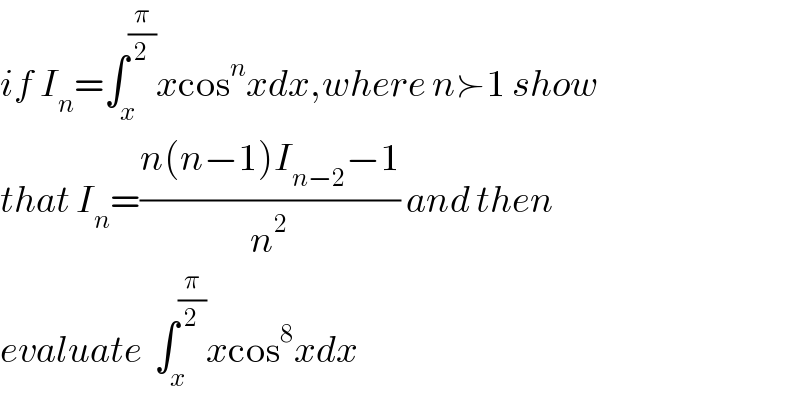 | ||
Answered by Olaf last updated on 23/Sep/20 | ||
![I_n = ∫_0 ^(π/2) xcos^n xdx I_n −I_(n+2) = ∫_0 ^(π/2) xcos^n x(1−cos^2 x)dx I_n −I_(n+2) = −∫_0 ^(π/2) (xsinx)(−sinxcos^n x)dx I_n −I_(n+2) = −[xsinx((cos^(n+1) x)/(n+1))]_0 ^(π/2) +∫_0 ^(π/2) (sinx+xcosx)((cos^(n+1) x)/(n+1))dx I_n −I_(n+2) = −∫_0 ^(π/2) (−sinx((cos^(n+1) x)/(n+1)))dx +(1/(n+1))I_(n+2) I_n −I_(n+2) = −[((cos^(n+2) x)/((n+1)(n+2)))]_0 ^(π/2) +(1/(n+1))I_(n+2) I_n = (1/((n+1)(n+2)))+I_(n+2) +(1/(n+1))I_(n+2) I_n = ((n+2)/(n+1))I_(n+2) +(1/((n+1)(n+2))) I_(n+2) = ((n+1)/(n+2))I_n −(1/((n+2)^2 )) (1) I_n = ((n(n−1)I_(n−2) −1)/n^2 ) I_0 = ∫_0 ^(π/2) xdx = [(x^2 /2)]_0 ^(π/2) = (π^2 /8) With (1) : I_2 = (1/2)((π^2 /8))−(1/4) = (π^2 /(16))−(1/4) I_4 = (3/4)((π^2 /(16))−(1/4))−(1/(16)) = ((3π^2 )/(64))−(1/4) I_6 = (5/6)(((3π^2 )/(64))−(1/4))−(1/(36)) = ((5π^2 )/(128))−((17)/(72)) I_8 = (7/8)(((5π^2 )/(128))−((17)/(72)))−(1/(64)) = ((35π^2 )/(1024))−(2/9) I_8 = ∫_0 ^(π/2) xcos^8 xdx = ((35π^2 )/(1024))−(2/9)](Q115155.png) | ||
| ||
Commented by Tawa11 last updated on 06/Sep/21 | ||
 | ||