
Question and Answers Forum
Question Number 115026 by jm2bok last updated on 23/Sep/20
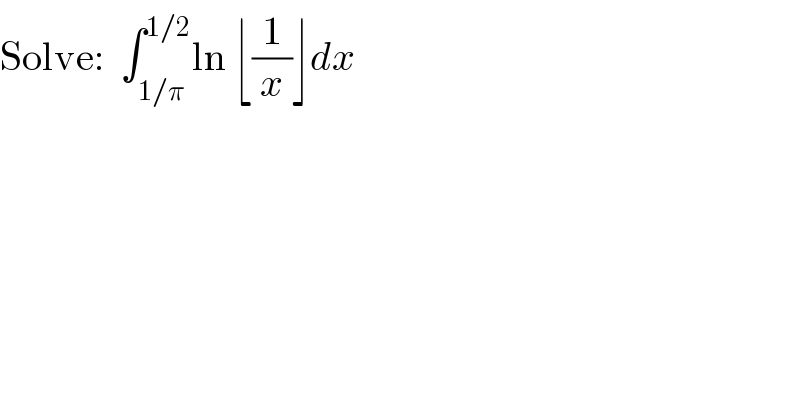
Answered by PRITHWISH SEN 2 last updated on 23/Sep/20

Answered by mathmax by abdo last updated on 23/Sep/20
![I =∫_(1/π) ^(1/2) ln{[(1/x)]}dx we do the changement (1/x)=t ⇒ I =∫_π ^2 ln{[t]}(−(dt/t^2 )) =∫_2 ^π ((ln[t])/t^2 ) dt (π∼3,14) ⇒ I =∫_2 ^3 ((ln[t])/t^2 )dt +∫_3 ^π ((ln[t])/t^2 )dt =2 ∫_2 ^3 (dt/t^2 ) +3 ∫_3 ^π (dt/t^2 ) =2[−(1/t)]_2 ^3 +3[−(1/t)]_3 ^π =2((1/2)−(1/3)) +3((1/3)−(1/π)) =1−(2/3) +1−(3/π) =2−(2/3)−(3/π) =(4/3)−(3/π)](Q115089.png)
| ||
Question and Answers Forum | ||
Question Number 115026 by jm2bok last updated on 23/Sep/20 | ||
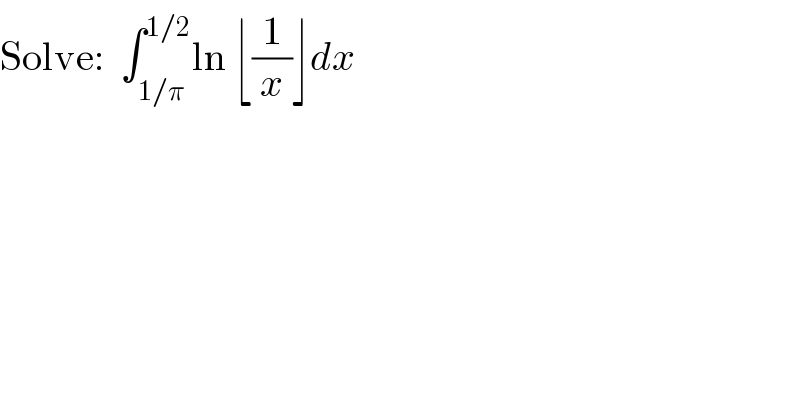 | ||
Answered by PRITHWISH SEN 2 last updated on 23/Sep/20 | ||
 | ||
| ||
Answered by mathmax by abdo last updated on 23/Sep/20 | ||
![I =∫_(1/π) ^(1/2) ln{[(1/x)]}dx we do the changement (1/x)=t ⇒ I =∫_π ^2 ln{[t]}(−(dt/t^2 )) =∫_2 ^π ((ln[t])/t^2 ) dt (π∼3,14) ⇒ I =∫_2 ^3 ((ln[t])/t^2 )dt +∫_3 ^π ((ln[t])/t^2 )dt =2 ∫_2 ^3 (dt/t^2 ) +3 ∫_3 ^π (dt/t^2 ) =2[−(1/t)]_2 ^3 +3[−(1/t)]_3 ^π =2((1/2)−(1/3)) +3((1/3)−(1/π)) =1−(2/3) +1−(3/π) =2−(2/3)−(3/π) =(4/3)−(3/π)](Q115089.png) | ||
| ||