
Question and Answers Forum
Question Number 115030 by bobhans last updated on 23/Sep/20
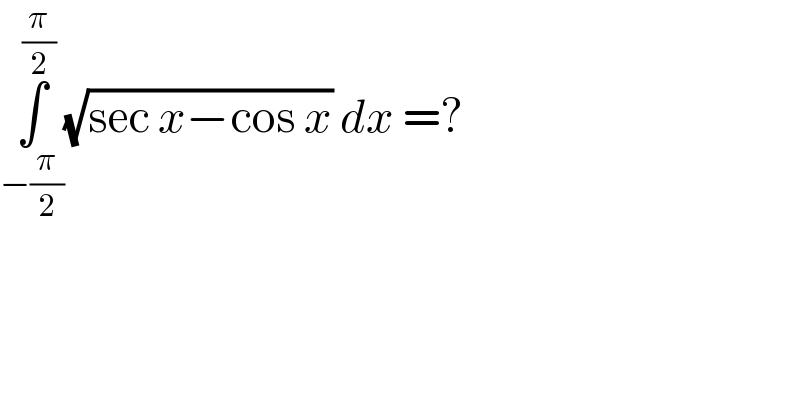
Answered by bemath last updated on 23/Sep/20
![∫_(−(π/2)) ^(π/2) (√((1−cos^2 x)/(cos x))) dx = ∫_(−(π/2)) ^(π/2) ((∣sin x∣)/( (√(cos x)))) dx = −∫_(−(π/2)) ^0 ((sin x)/( (√(cos x)))) dx + ∫_0 ^(π/2) ((sin x)/( (√(cos x)))) dx = ∫_(−(π/2)) ^0 ((d(cos x))/( (√(cos x)))) −∫_0 ^(π/2) ((d(cos x))/( (√(cos x)))) = 2 [ (√(cos x )) ]_(−(π/2)) ^( 0) −2 [ (√(cos x )) ] _0^(π/2) = 2 −2(0−1) = 4](Q115032.png)
Answered by mathmax by abdo last updated on 23/Sep/20
![A =∫_(−(π/2)) ^(π/2) (√((1/(cosx))−cosx))dx ⇒A =2∫_0 ^(π/2) (√((1−cos^2 x)/(cosx)))dx =2 ∫_0 ^(π/2) ((∣sinx∣)/(√(cosx)))dx =2 ∫_0 ^(π/2) ((sinx)/(√(cosx)))dx =2[−2(√(cosx))]_0 ^(π/2) =2{2} =4](Q115088.png)
| ||
Question and Answers Forum | ||
Question Number 115030 by bobhans last updated on 23/Sep/20 | ||
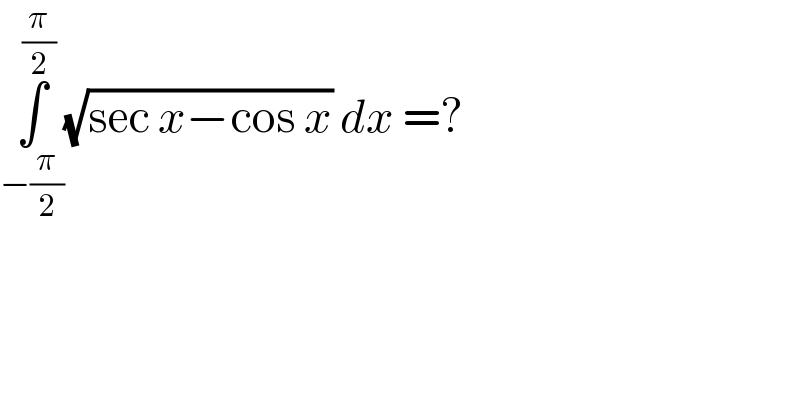 | ||
Answered by bemath last updated on 23/Sep/20 | ||
![∫_(−(π/2)) ^(π/2) (√((1−cos^2 x)/(cos x))) dx = ∫_(−(π/2)) ^(π/2) ((∣sin x∣)/( (√(cos x)))) dx = −∫_(−(π/2)) ^0 ((sin x)/( (√(cos x)))) dx + ∫_0 ^(π/2) ((sin x)/( (√(cos x)))) dx = ∫_(−(π/2)) ^0 ((d(cos x))/( (√(cos x)))) −∫_0 ^(π/2) ((d(cos x))/( (√(cos x)))) = 2 [ (√(cos x )) ]_(−(π/2)) ^( 0) −2 [ (√(cos x )) ] _0^(π/2) = 2 −2(0−1) = 4](Q115032.png) | ||
| ||
Answered by mathmax by abdo last updated on 23/Sep/20 | ||
![A =∫_(−(π/2)) ^(π/2) (√((1/(cosx))−cosx))dx ⇒A =2∫_0 ^(π/2) (√((1−cos^2 x)/(cosx)))dx =2 ∫_0 ^(π/2) ((∣sinx∣)/(√(cosx)))dx =2 ∫_0 ^(π/2) ((sinx)/(√(cosx)))dx =2[−2(√(cosx))]_0 ^(π/2) =2{2} =4](Q115088.png) | ||
| ||