
Question and Answers Forum
Question Number 115055 by mnjuly1970 last updated on 23/Sep/20
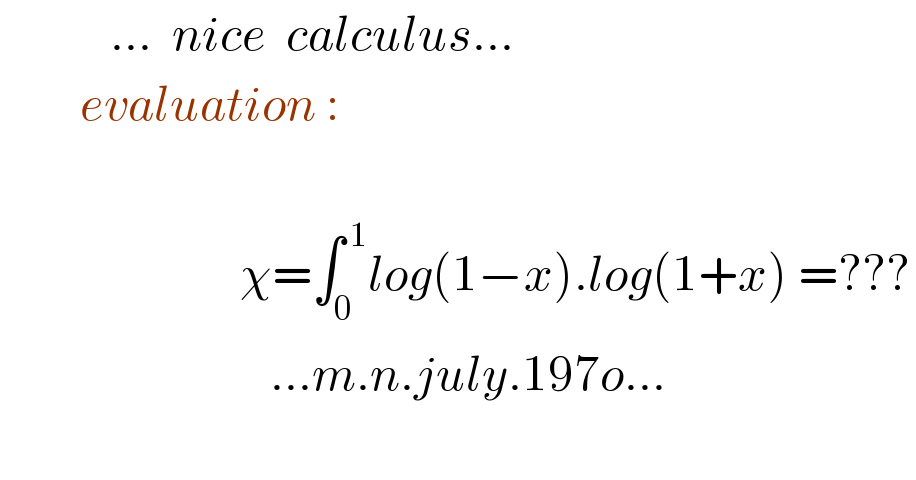
Answered by mathmax by abdo last updated on 23/Sep/20
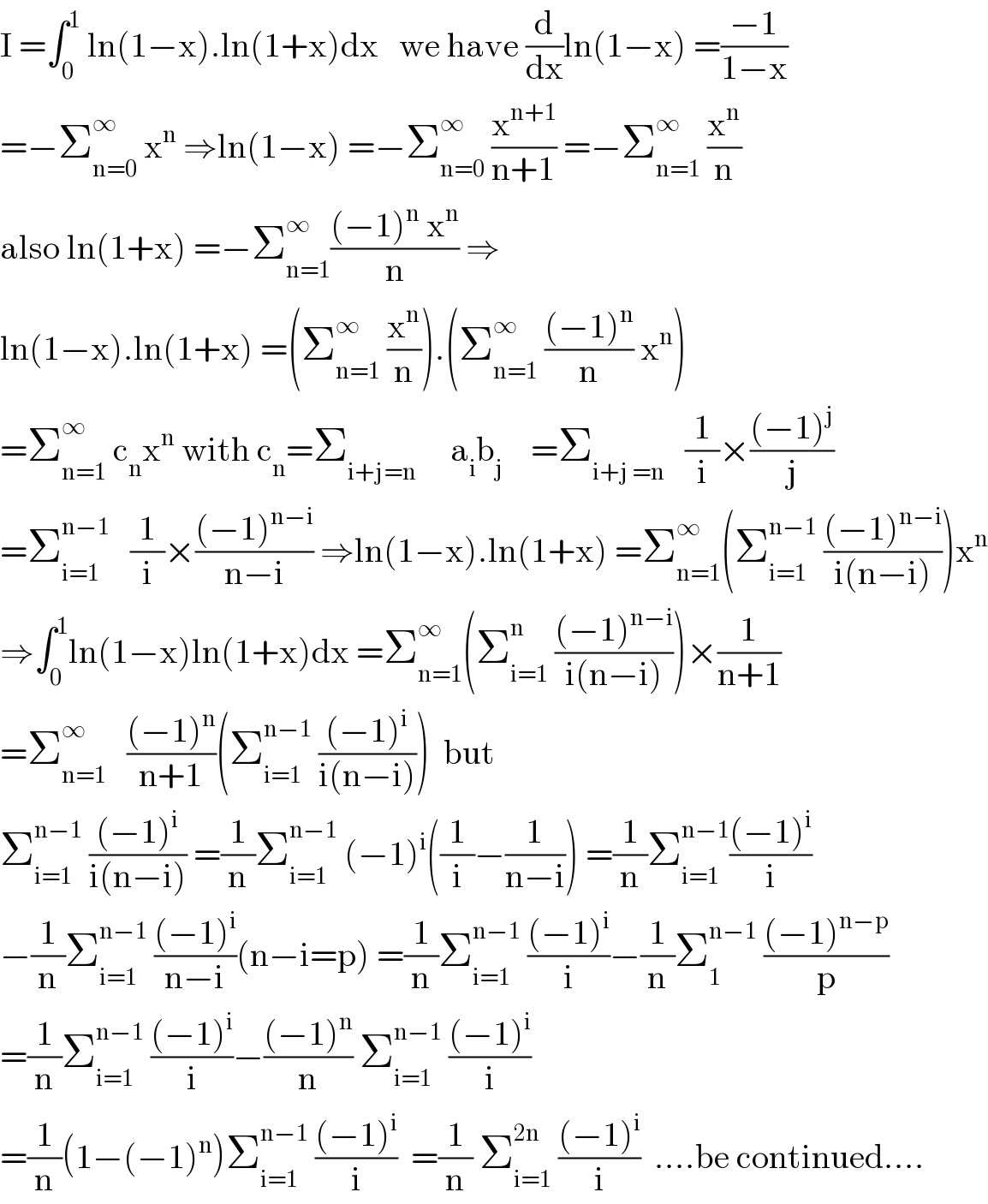
Commented by mnjuly1970 last updated on 23/Sep/20
Commented by mathmax by abdo last updated on 23/Sep/20

Answered by mathdave last updated on 23/Sep/20
![solution if let I_1 =∫_0 ^1 ln(1−x)ln(1+x)dx.....(1) put x=−x I_2 =∫_(−1) ^0 ln(1+x)ln(1−x)dx........(2) since the integrand are unchanged then we add them up which mean that I_1 =I_2 I=I_1 +I_2 =2I_1 , I_1 =(1/2)I I_1 =∫_0 ^1 ln(1−x)ln(1+x)dx=(1/2)∫_0 ^1 ln(1−x)ln(1+x)dx put x=2y−1,dx=2dy I_1 =(1/2)∫_0 ^1 ln(2−2y)ln(2y)2dy=∫_0 ^1 [(ln2+ln(1−y))(ln2+lny)]dy I=∫_0 ^1 (ln^2 2+ln2(ln(1−y)+lny)+lnyln(1−y))dx I=ln^2 (2)∫_0 ^1 dy+ln2∫_0 ^1 (lny+ln(1−y))dy+∫_0 ^1 lnyln(1−y)dy let A=ln^2 (2)∫_0 ^1 dy=ln^2 (2)......(1) let B=ln2∫_0 ^1 (lny+ln(1−y))dy=2∫_0 ^1 lnydy B=2ln2(ylny−y)_0 ^1 =−2ln2.....(2) let C=∫_0 ^1 lnyln(1−y)dy=−Σ_(n=1) ^∞ (1/n)∫_0 ^1 y^n lnydy C=−Σ_(n=1) ^∞ (1/n)(∂/∂a)∣_(a=1) ∫_0 ^1 y^n .y^(a−1) dy=−Σ_(n=1) ^∞ (1/n)(∂/∂a)∣_(a=1) ((1/(n+a))) C=Σ_(n=1) ^∞ (1/(n(n+1)^2 ))=Σ_(n=1) ^∞ ((1/n)−(1/(n+1))−(1/((n+1)^2 ))) C=Σ_(n=1) ^∞ (1/n)−Σ_(n=2) ^∞ (1/n)−Σ_(n=2) ^∞ (1/n^2 )=Σ_(n=1) ^∞ ((1/n))−Σ_(n=1) ^∞ ((1/n)−1)−Σ_(n=1) ^∞ ((π^2 /6)−1) C=1−(π^2 /6)+1=(2−(π^2 /6)).........(3) but I=A+B+C=ln^2 (2)−2ln2+2−(π^2 /6)=2−(π^2 /6)+ln^2 (2)−ln4 ∵∫_0 ^1 ln(1−x)ln(1+x)dx=2−(π^2 /6)+ln^2 (2)−ln4 by mathdave(23/09/2020)](Q115107.png)
Commented by mnjuly1970 last updated on 23/Sep/20
Commented by mnjuly1970 last updated on 23/Sep/20
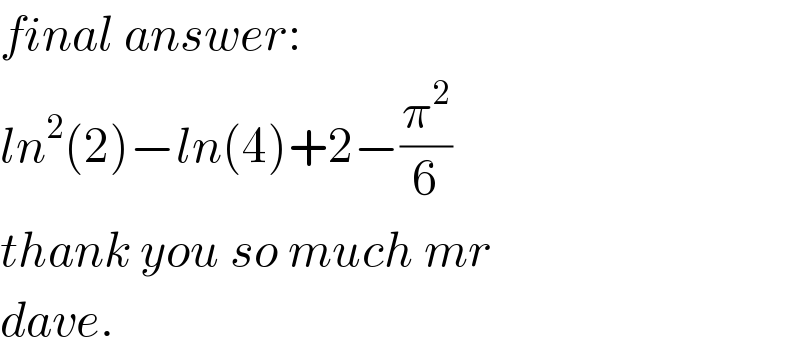
Commented by mnjuly1970 last updated on 23/Sep/20

Commented by Tawa11 last updated on 06/Sep/21

