Question Number 115111 by mnjuly1970 last updated on 23/Sep/20
$$\:\:\:\:\:\:\:\:\:\:\:\:\:...{mathematical}\:\:{analysis}...\:\:\:\:\: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{prove}\:\:{that}: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left({x}^{\mathrm{8}} +\mathrm{1}\right){ln}\left({x}\right)}{{x}^{\mathrm{10}} −\mathrm{1}}\:{dx}=\frac{\pi^{\mathrm{2}} \varphi^{\mathrm{2}} }{\mathrm{25}}\:\:\checkmark \\ $$$$\:\:\:\:\:\:\:\:\:\:{m}.{n}.{july}\:\mathrm{1970} \\ $$$$ \\ $$
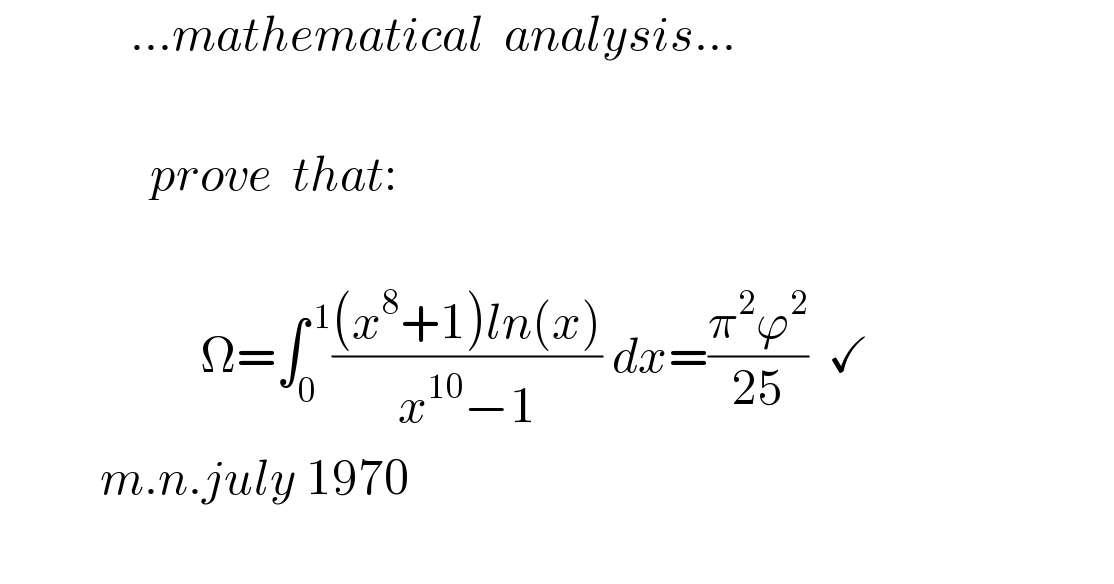
Answered by Olaf last updated on 23/Sep/20
![∫((1+x^8 )/(1−x^(10) ))dx = ∫(1+x^8 )Σ_(n=0) ^∞ x^(10n) dx = Σ_(n=0) ^∞ ((x^(10n+1) /(10n+1))+(x^(10n+9) /(10n+9))) Ω = [−Σ_(n=0) ^∞ ((x^(10n+1) /(10n+1))+(x^(10n+9) /(10n+9)))lnx]_0 ^1 +∫_0 ^1 Σ_(n=0) ^∞ ((x^(10n+1) /(10n+1))+(x^(10n+9) /(10n+9)))(dx/x) Ω = ∫_0 ^1 Σ_(n=0) ^∞ ((x^(10n) /(10n+1))+(x^(10n+8) /(10n+9)))dx Ω = Σ_(n=0) ^∞ [(x^(10n+1) /((10n+1)^2 ))+(x^(10n+9) /((10n+9)^2 ))]_0 ^1 Ω = Σ_(n=0) ^∞ [(1/((10n+1)^2 ))+(1/((10n+9)^2 ))] work in progress...](Q115134.png)
$$\int\frac{\mathrm{1}+{x}^{\mathrm{8}} }{\mathrm{1}−{x}^{\mathrm{10}} }{dx}\:=\:\int\left(\mathrm{1}+{x}^{\mathrm{8}} \right)\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{\mathrm{10}{n}} {dx} \\ $$$$=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{{x}^{\mathrm{10}{n}+\mathrm{1}} }{\mathrm{10}{n}+\mathrm{1}}+\frac{{x}^{\mathrm{10}{n}+\mathrm{9}} }{\mathrm{10}{n}+\mathrm{9}}\right) \\ $$$$\Omega\:=\:\left[−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{{x}^{\mathrm{10}{n}+\mathrm{1}} }{\mathrm{10}{n}+\mathrm{1}}+\frac{{x}^{\mathrm{10}{n}+\mathrm{9}} }{\mathrm{10}{n}+\mathrm{9}}\right)\mathrm{ln}{x}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$+\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{{x}^{\mathrm{10}{n}+\mathrm{1}} }{\mathrm{10}{n}+\mathrm{1}}+\frac{{x}^{\mathrm{10}{n}+\mathrm{9}} }{\mathrm{10}{n}+\mathrm{9}}\right)\frac{{dx}}{{x}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{{x}^{\mathrm{10}{n}} }{\mathrm{10}{n}+\mathrm{1}}+\frac{{x}^{\mathrm{10}{n}+\mathrm{8}} }{\mathrm{10}{n}+\mathrm{9}}\right){dx} \\ $$$$\Omega\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{{x}^{\mathrm{10}{n}+\mathrm{1}} }{\left(\mathrm{10}{n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{x}^{\mathrm{10}{n}+\mathrm{9}} }{\left(\mathrm{10}{n}+\mathrm{9}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\Omega\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{\mathrm{1}}{\left(\mathrm{10}{n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{10}{n}+\mathrm{9}\right)^{\mathrm{2}} }\right] \\ $$$${work}\:{in}\:{progress}... \\ $$
Commented by mnjuly1970 last updated on 23/Sep/20
$${very}\:{nice}\:\:.{thanks}... \\ $$
Commented by maths mind last updated on 24/Sep/20
$$\Omega=\frac{\mathrm{1}}{\mathrm{100}}\left(\Sigma\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{1}}{\mathrm{10}}\right)^{\mathrm{2}} }+\Sigma\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{9}}{\mathrm{10}}\right)^{\mathrm{2}} }\right)...{sir}\:{olaf}\:{done}\:{all}\:{worck} \\ $$$$=\frac{\Psi_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{10}}\right)+\Psi_{\mathrm{1}} \left(\frac{\mathrm{9}}{\mathrm{10}}\right)}{\mathrm{100}} \\ $$$$\Psi_{\mathrm{1}} \left({z}\right)+\Psi_{\mathrm{1}} \left(\mathrm{1}−{z}\right)=\frac{\pi^{\mathrm{2}} }{{sin}^{\mathrm{2}} \left(\pi{z}\right)}\:\:,{z}=\frac{\mathrm{1}}{\mathrm{10}} \\ $$$${give}\:{usanswer}\: \\ $$$$ \\ $$
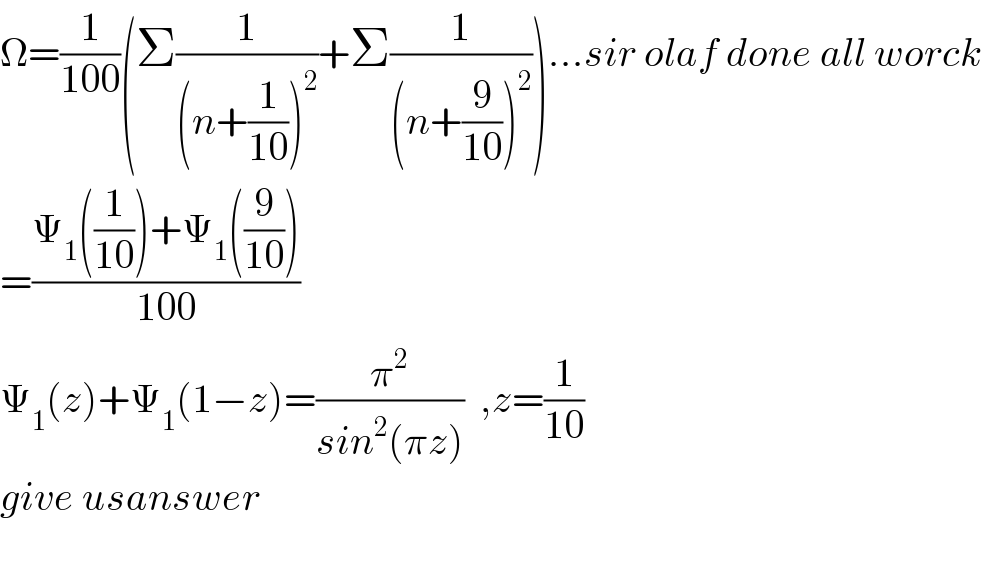
Answered by mathdave last updated on 24/Sep/20
![solution let I=∫_0 ^1 (((x^8 +1)lnx)/(x^(10) −1))dx=−∫_0 ^1 ((x^8 lnx)/(1−x^(10) ))dx−∫_0 ^1 ((lnx)/(1−x^(10) ))dx I=−Σ_(n=0) ^∞ ∫_0 ^1 x^8 .x^(10n) .lnxdx−Σ_(n=0) ^∞ ∫^1 _0 x^(10n) lnxdx I=−Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ∫_0 ^1 x^(10n+8) .x^(a−1) dx−Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ∫_0 ^1 x^(10n) .x^(a−1) dx I=−Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ((1/(10n+8+a)))−Σ_(n=0) ^∞ (∂/∂a)∣_(a=1) ((1/(10n+a))) I=Σ_(n=0) ^∞ (1/((10n+9)^2 ))+Σ_(n=0) ^∞ (1/((10n+1)^2 ))=Σ_(n=−∞) ^∞ (1/((10n+1)^2 )) I=Σ_(n=−∞) ^∞ (1/((10n+1)^2 ))=−(π/(100))lim_(z→−(1/(10))) (1/(1!))(d/dz)(cot(πz) I=−(π/(100))lim_(z→−(1/(10)) ) −πcosec^2 (−(π/(10)))=(π^2 /(100))•(1/(sin^2 ((π/(10))))) let ((90)/5)=18 let x=18 ∵90=5x=2x+3x 90−3x=2x ,sin(90−3x)=sin(2x) cos(3x)=sin(2x) 4cos^3 x−3cosx=2sinxcosx ,4cos^2 x−3=2sinx 4(1−sin^2 x)−3=2sinx ,4sin^2 x+2sinx−1=0 sinx=((−2±(√(4+16)))/8)=((−1+(√5))/4) ∵sin18=sin((π/(10)))=((−1+(√5))/4) sin^2 ((π/(10)))=[((−1+(√5))/4)]^2 =((3−(√5))/8) I=(π^2 /(100))•(1/(sin^2 ((π/(10)))))=(π^2 /(100))•(8/((3−(√(5)))))=(π^2 /(25))•(1/(((3/2)−((√5)/2)))) by linear approximation method of (a+b)^n =(a+nb) I=(π^2 /(25))•((3/2)−((√5)/2))^(−1) =(π^2 /(25))((3/2)+((√5)/2)) but ((1/2)+((√5)/2))^2 =((3/2)+((√5)/2)) note φ^2 =((1/2)+((√5)/2))^2 ∵I=∫_0 ^1 (((x^8 +1)lnx)/(x^(10) −1))dx=(π^2 /(25))φ^2 Q.E.D by mathdave(24/09/2020)](Q115161.png)
$${solution} \\ $$$${let} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({x}^{\mathrm{8}} +\mathrm{1}\right)\mathrm{ln}{x}}{{x}^{\mathrm{10}} −\mathrm{1}}{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{8}} \mathrm{ln}{x}}{\mathrm{1}−{x}^{\mathrm{10}} }{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}{x}}{\mathrm{1}−{x}^{\mathrm{10}} }{dx} \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{8}} .{x}^{\mathrm{10}{n}} .\mathrm{ln}{xdx}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\underset{\mathrm{0}} {\int}^{\mathrm{1}} {x}^{\mathrm{10}{n}} \mathrm{ln}{xdx} \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{10}{n}+\mathrm{8}} .{x}^{{a}−\mathrm{1}} {dx}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{10}{n}} .{x}^{{a}−\mathrm{1}} {dx} \\ $$$${I}=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{10}{n}+\mathrm{8}+{a}}\right)−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\partial}{\partial{a}}\mid_{{a}=\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{10}{n}+{a}}\right) \\ $$$${I}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{10}{n}+\mathrm{9}\right)^{\mathrm{2}} }+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{10}{n}+\mathrm{1}\right)^{\mathrm{2}} }=\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{10}{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${I}=\underset{{n}=−\infty} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{10}{n}+\mathrm{1}\right)^{\mathrm{2}} }=−\frac{\pi}{\mathrm{100}}\underset{{z}\rightarrow−\frac{\mathrm{1}}{\mathrm{10}}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{1}!}\frac{{d}}{{dz}}\left(\mathrm{cot}\left(\pi{z}\right)\right. \\ $$$${I}=−\frac{\pi}{\mathrm{100}}\underset{{z}\rightarrow−\frac{\mathrm{1}}{\mathrm{10}}\:} {\mathrm{lim}}−\pi\mathrm{cosec}^{\mathrm{2}} \left(−\frac{\pi}{\mathrm{10}}\right)=\frac{\pi^{\mathrm{2}} }{\mathrm{100}}\bullet\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{10}}\right)} \\ $$$${let}\:\frac{\mathrm{90}}{\mathrm{5}}=\mathrm{18}\:\:{let}\:{x}=\mathrm{18}\:\:\:\because\mathrm{90}=\mathrm{5}{x}=\mathrm{2}{x}+\mathrm{3}{x} \\ $$$$\mathrm{90}−\mathrm{3}{x}=\mathrm{2}{x}\:\:\:\:,\mathrm{sin}\left(\mathrm{90}−\mathrm{3}{x}\right)=\mathrm{sin}\left(\mathrm{2}{x}\right) \\ $$$$\mathrm{cos}\left(\mathrm{3}{x}\right)=\mathrm{sin}\left(\mathrm{2}{x}\right) \\ $$$$\mathrm{4co}{s}^{\mathrm{3}} {x}−\mathrm{3cos}{x}=\mathrm{2sin}{x}\mathrm{cos}{x}\:\:\:,\mathrm{4cos}^{\mathrm{2}} {x}−\mathrm{3}=\mathrm{2sin}{x} \\ $$$$\mathrm{4}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} {x}\right)−\mathrm{3}=\mathrm{2sin}{x}\:\:\:,\mathrm{4sin}^{\mathrm{2}} {x}+\mathrm{2sin}{x}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{sin}{x}=\frac{−\mathrm{2}\pm\sqrt{\mathrm{4}+\mathrm{16}}}{\mathrm{8}}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\because\mathrm{sin18}=\mathrm{sin}\left(\frac{\pi}{\mathrm{10}}\right)=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{10}}\right)=\left[\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}\right]^{\mathrm{2}} =\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$${I}=\frac{\pi^{\mathrm{2}} }{\mathrm{100}}\bullet\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{10}}\right)}=\frac{\pi^{\mathrm{2}} }{\mathrm{100}}\bullet\frac{\mathrm{8}}{\left(\mathrm{3}−\sqrt{\left.\mathrm{5}\right)}\right.}=\frac{\pi^{\mathrm{2}} }{\mathrm{25}}\bullet\frac{\mathrm{1}}{\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)}\: \\ $$$${by}\:{linear}\:{approximation}\:{method}\:{of} \\ $$$$\left({a}+{b}\right)^{{n}} =\left({a}+{nb}\right) \\ $$$${I}=\frac{\pi^{\mathrm{2}} }{\mathrm{25}}\bullet\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{−\mathrm{1}} =\frac{\pi^{\mathrm{2}} }{\mathrm{25}}\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$$${but}\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} =\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\:\:\:\:\:{note}\:\phi^{\mathrm{2}} =\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\because{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({x}^{\mathrm{8}} +\mathrm{1}\right)\mathrm{ln}{x}}{{x}^{\mathrm{10}} −\mathrm{1}}{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{25}}\phi^{\mathrm{2}} \:\:\:\:\:{Q}.{E}.{D} \\ $$$${by}\:{mathdave}\left(\mathrm{24}/\mathrm{09}/\mathrm{2020}\right) \\ $$
Commented by mnjuly1970 last updated on 24/Sep/20
$${very}\:{nice}\:{and}\:{perfect}\:\:{mr}\: \\ $$$${dave}..{thx}\:{a}\:{lot}.. \\ $$
Commented by Tawa11 last updated on 06/Sep/21
$$\mathrm{great} \\ $$