
Question and Answers Forum
Question Number 115238 by bemath last updated on 24/Sep/20
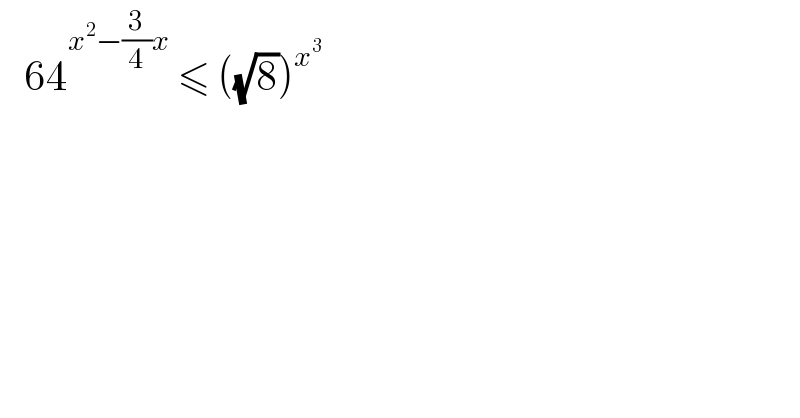
Answered by Rasheed.Sindhi last updated on 24/Sep/20
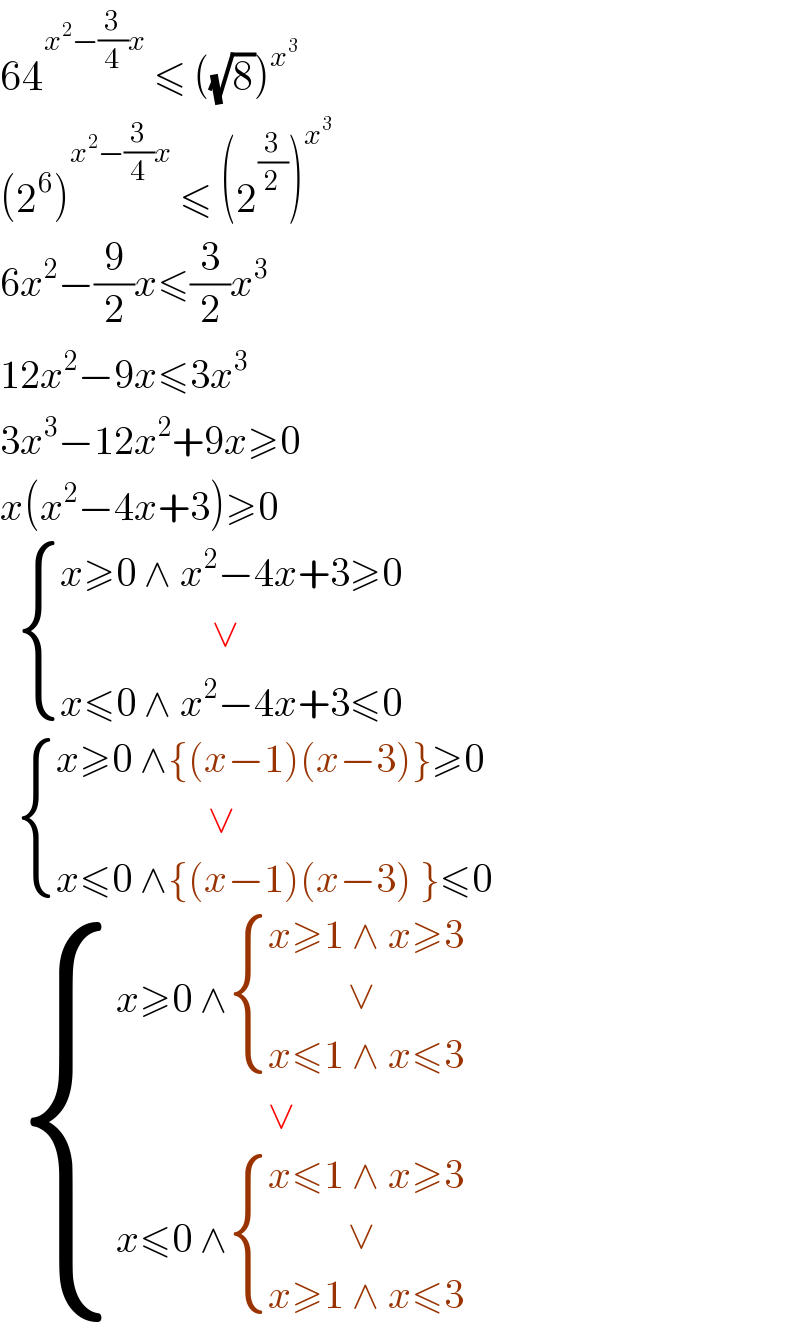
Commented by bemath last updated on 24/Sep/20

Answered by Olaf last updated on 24/Sep/20
![x(x−1)(x−3) ≥ 0 (1) ⇔ x∈[0;1]∪[3;+∞[ Then (1) : x(x^2 −4x+3) ≥ 0 x^3 −4x^2 +3x ≥ 0 4x^2 −3x ≤ x^3 (3/2)(4x^2 −3x) ≤ (3/2)x^3 6(x^2 −(3/4)x) ≤ (3/2)x^3 6ln2(x^2 −(3/4)x) ≤ ((3/2)ln2)x^3 (x^2 −(3/4)x)ln64 ≤ x^3 ln(√8) ln64^(x^2 −(3/4)x) ≤ ln((√8))^x^3 64^(x^2 −(3/4)x) ≤( (√8))^x^3 S = [0;1]∪[3;+∞[](Q115243.png)
| ||
Question and Answers Forum | ||
Question Number 115238 by bemath last updated on 24/Sep/20 | ||
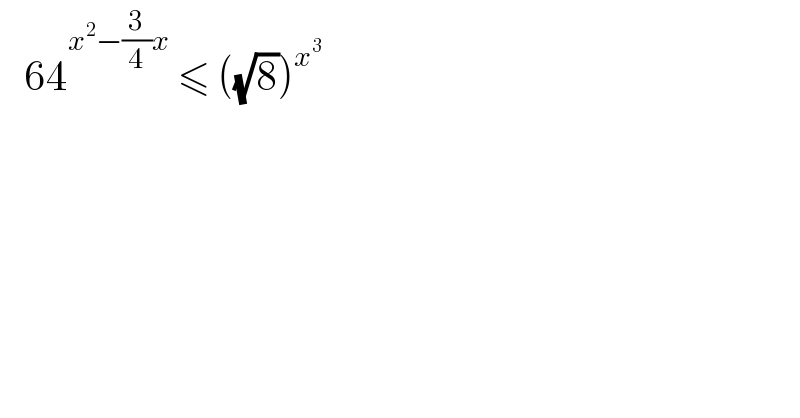 | ||
Answered by Rasheed.Sindhi last updated on 24/Sep/20 | ||
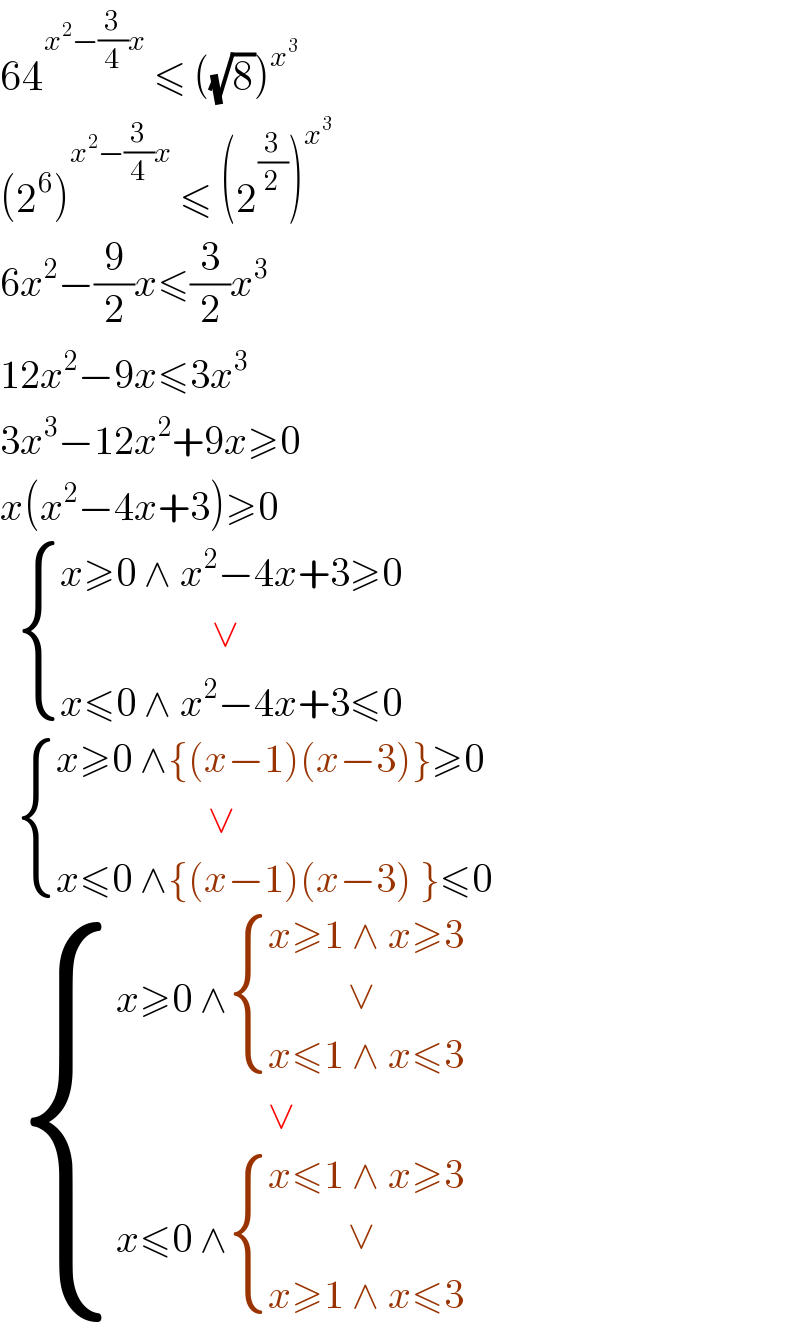 | ||
| ||
Commented by bemath last updated on 24/Sep/20 | ||
 | ||
Answered by Olaf last updated on 24/Sep/20 | ||
![x(x−1)(x−3) ≥ 0 (1) ⇔ x∈[0;1]∪[3;+∞[ Then (1) : x(x^2 −4x+3) ≥ 0 x^3 −4x^2 +3x ≥ 0 4x^2 −3x ≤ x^3 (3/2)(4x^2 −3x) ≤ (3/2)x^3 6(x^2 −(3/4)x) ≤ (3/2)x^3 6ln2(x^2 −(3/4)x) ≤ ((3/2)ln2)x^3 (x^2 −(3/4)x)ln64 ≤ x^3 ln(√8) ln64^(x^2 −(3/4)x) ≤ ln((√8))^x^3 64^(x^2 −(3/4)x) ≤( (√8))^x^3 S = [0;1]∪[3;+∞[](Q115243.png) | ||
| ||