Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 115273 by mnjuly1970 last updated on 24/Sep/20

$$...advancedmathematics...$$$$$$$$evaluate:::$$$$$$$$\mathrm{\Delta }={\int }_0^{\mathrm{\infty }}\frac{cos\left(ln\left(x\right)\right)}{{(x+1)}^2}dx=???$$$$$$$$...m.n.july.1970...$$$$$$

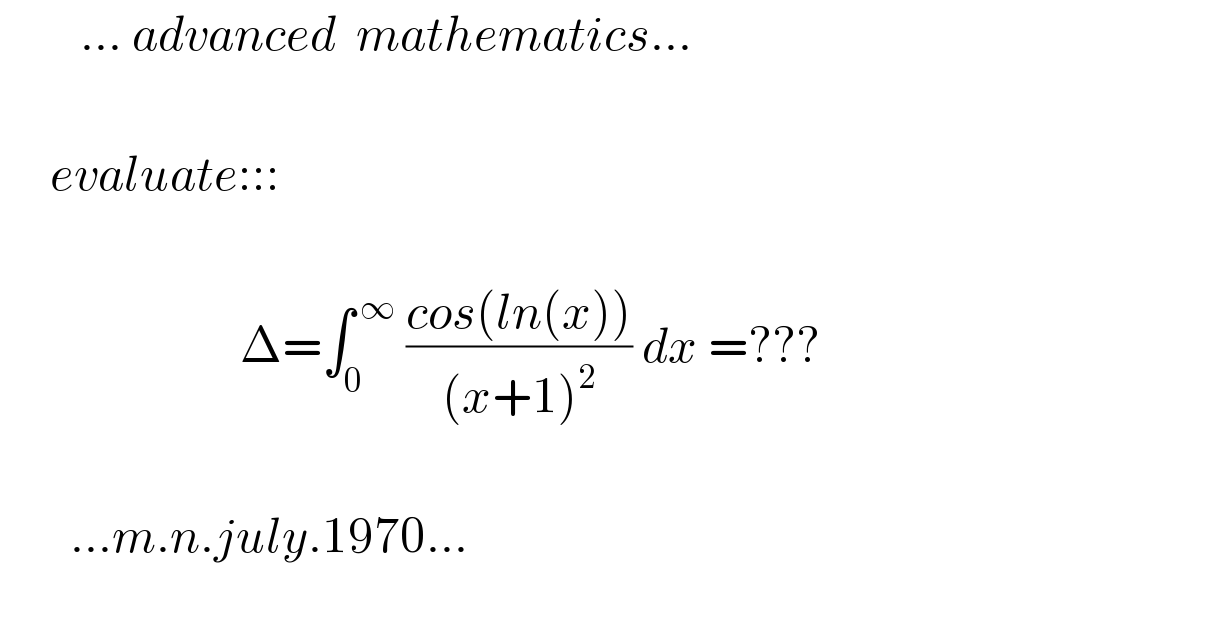
Answered by Bird last updated on 24/Sep/20

$$A={\int }_0^{\mathrm{\infty }}\frac{cos\left(lnx\right)}{{(x+1)}^2}dx\Rightarrow$$$$A={\int }_0^1\frac{cos\left(lnx\right)}{{(x+1)}^2}dx+{\int }_1^{\mathrm{\infty }}\frac{cos\left(lnx\right)}{{(x+1)}^2}dx$$$$but{\int }_1^{\mathrm{\infty }}\frac{cos\left(lnx\right)}{{(x+1)}^2}dx{=}_{x=\frac{1}{t}}$$$$-{\int }_0^1\frac{cos\left(lnt\right)}{{(\frac{1}{t}+1)}^2}(-\frac{dt}{t^2})$$$$={\int }_0^1\frac{cos\left(lnx\right)}{{(x+1)}^2}\Rightarrow A=2{\int }_0^1\frac{cos\left(lnx\right)}{{(x+1)}^2}dx$$$$wehave\frac{1}{x+1}=\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n{x}^n$$$$\Rightarrow -\frac{1}{{(x+1)}^2}=\sum _{n=1}^{\mathrm{\infty }}{(-1)}^n{nx}^{n-1}$$$$\Rightarrow \frac{1}{{(x+1)}^2}=\sum _{n=1}^{\mathrm{\infty }}{(-1)}^{n-1}{nx}^{n-1}$$$$=\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n(n+1)x^n\Rightarrow$$$$A=2{\int }_0^1\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n(n+1)x^{n}cos\left(lnx\right)dx$$$$=2\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n(n+1){\int }_0^1{x}^{n}cos\left(lnx\right)dx$$$$U_n={\int }_0^1{x}^{n}cos\left(lnx\right)dx$$$${=}_{lnx=-t}-{\int }_0^{\mathrm{\infty }}{e}^{-nt}cos\left(t\right)(-e^{-t})dt$$$$={\int }_0^{\mathrm{\infty }}{e}^{-(n+1)t}cos\left(t\right)dt$$$$=Re\left({\int }_0^{\mathrm{\infty }}{e}^{-(n+1)t}{e}^{it}dt\right)but$$$${\int }_0^{\mathrm{\infty }}{e}^{(-(n+1)+i)t}dt$$$$={\left[\frac{1}{-(n+1)+i}{e}^{(-(n+1)+i)t}\right]}_0^{\mathrm{\infty }}$$$$=\frac{1}{n+1-i}=\frac{n+1+i}{{(n+1)}^2+1}\Rightarrow$$$$U_n=\frac{n+1}{{(n+1)}^2+1}\Rightarrow$$$$A=2\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n(n+1)\times \frac{n+1}{{(n+1)}^2+1}$$$$=\sum _{n=0}^{\mathrm{\infty }}{(-1)}^n\frac{{(n+1)}^2}{{(n+1)}^2+1}$$$$=\sum _{n=1}^{\mathrm{\infty }}{(-1)}^{n-1}.\frac{n^2}{n^2+1}$$$$=\sum _{n=1}^{\mathrm{\infty }}{(-1)}^{n-1}(1-\frac{1}{n^2+1})$$$$=\sum _{n=1}^{\mathrm{\infty }}{(-1)}^{n-1}(\to diverges)+\sum _{n=1}^{\mathrm{\infty }}\frac{{(-1)}^n}{n^2+1}\left(converges\right)$$$$perhspsthisintegralisdivergent..!$$

Commented by mnjuly1970 last updated on 24/Sep/20

Commented by mnjuly1970 last updated on 24/Sep/20

$$integralisconvergent\Uparrow \Uparrow \Uparrow$$

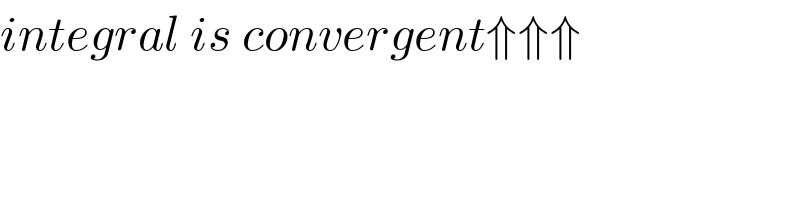
Commented by Dwaipayan Shikari last updated on 24/Sep/20

$$\underset{\mathrm{n}=1}{\sum ^{\mathrm{\infty }}}{(-1)}^{\mathrm{n}-1}=1-1+1-1+1-1+...$$$$\mathrm{Sum}{\mathrm{doesn}}^{\prime }\mathrm{t}\mathrm{exist}\mathrm{or}$$$$1-1+1-1+1-1+1-1=\frac{1}{2}\left(\mathrm{Analytical}\mathrm{continuation}\right)$$

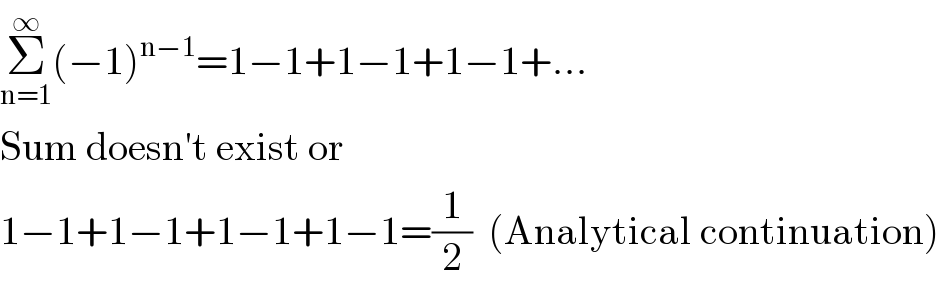
Commented by Olaf last updated on 24/Sep/20

$${\mathrm{U}}_n={\int }_0^1{x}^n\cos \left(\ln x\right)dx={\int }_0^1{x}^{n+1}\frac{\cos \left(\ln x\right)}{x}dx$$$${\mathrm{U}}_n={\left[x^{n+1}\sin \left(\ln x\right)\right]}_0^1-{\int }_0^1(n+1)x^n\sin \left(\ln x\right)dx$$$${\mathrm{U}}_n=-(n+1){\int }_0^1{x}^{n+1}\frac{\sin \left(\ln x\right)}{x}dx$$$${\mathrm{U}}_n=-(n+1)\{{[-x^{n+1}\cos \left(\ln x\right)]}_0^1+(n+1){\int }_0^1{x}^n\cos \left(\ln x\right)dx\}$$$${\mathrm{U}}_n=-(n+1)(-1+(n+1){\mathrm{U}}_n)$$$$(1+{(n+1)}^2){\mathrm{U}}_n=n+1$$$${\mathrm{U}}_n=\frac{n+1}{{(n+1)}^2+1}$$$$maybe...$$$$$$

Commented by Bird last updated on 24/Sep/20

$$postyouanswersir$$

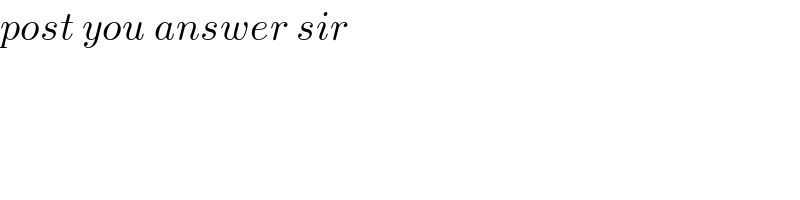
Commented by mnjuly1970 last updated on 24/Sep/20

$$ok.isentmysolution.$$

Commented by mnjuly1970 last updated on 24/Sep/20

Commented by Bird last updated on 25/Sep/20

$$okthanks$$

Answered by mnjuly1970 last updated on 24/Sep/20

$$solution$$$$\mathrm{\Delta }=\mathcal{R}e{\int }_0^{\mathrm{\infty }}\frac{e^{iln\left(x\right)}}{{(x+1)}^2}dx=\mathcal{R}e{\int }_0^{\mathrm{\infty }}\frac{x^i}{{(x+1)}^2}dx$$$$=\mathcal{R}e{\int }_0^{\mathrm{\infty }}\frac{x^{(i+1)-1}}{{(x+1)}^2}dx=\mathcal{R}e\left(\beta (1+i,1-i)\right)$$$$=\mathcal{R}e\frac{\mathrm{\Gamma }(1+i)\mathrm{\Gamma }(1-i)}{⟨\mathrm{\Gamma }\left(2\right)=1⟩}=$$$$\mathcal{R}e\left[i\mathrm{\Gamma }\left(i\right)\mathrm{\Gamma }(1-i)\right]\stackrel{eulerreflectionformula}{=}\mathcal{R}e\left[i\frac{\pi }{sin(i\pi }\right]$$$$=\mathcal{R}e\left[\frac{2i\left(i\pi \right)}{e^{i\left(i\pi \right)}-e^{-i\left(i\pi \right)}}\right]=\frac{-2\pi }{e^{-\pi }-e^{\pi }}$$$$=\frac{\pi }{\frac{e^{\pi }-e^{-\pi }}{2}}=\frac{\pi }{sinh\left(\pi \right)}✓$$$$m.n.july.1970$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com