
Question and Answers Forum
Question Number 115366 by Bird last updated on 25/Sep/20
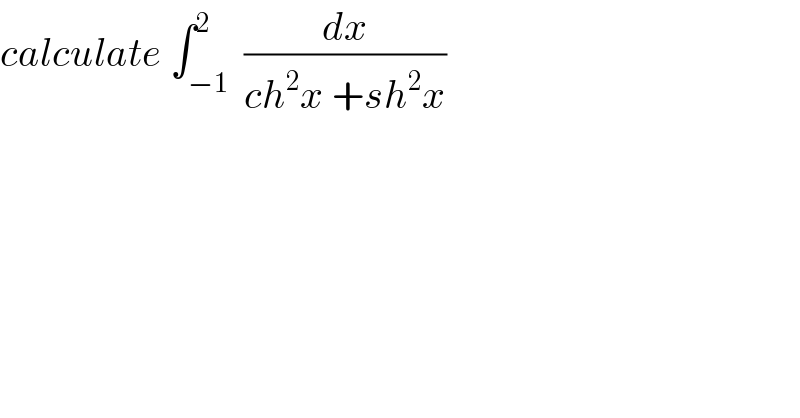
Answered by MJS_new last updated on 25/Sep/20
![∫(dx/(cosh^2 x +sinh^2 x))= [t=e^(2x) → dx=(dt/(2e^(2x) ))] =∫(dt/(t^2 +1))=arctan t = =arctan e^(2x) +C ∫_(−1) ^2 (dx/(cosh^2 x +sinh^2 x))=arctan e^4 −arctan e^(−2)](Q115379.png)
Commented by mathmax by abdo last updated on 25/Sep/20

Answered by mathmax by abdo last updated on 25/Sep/20
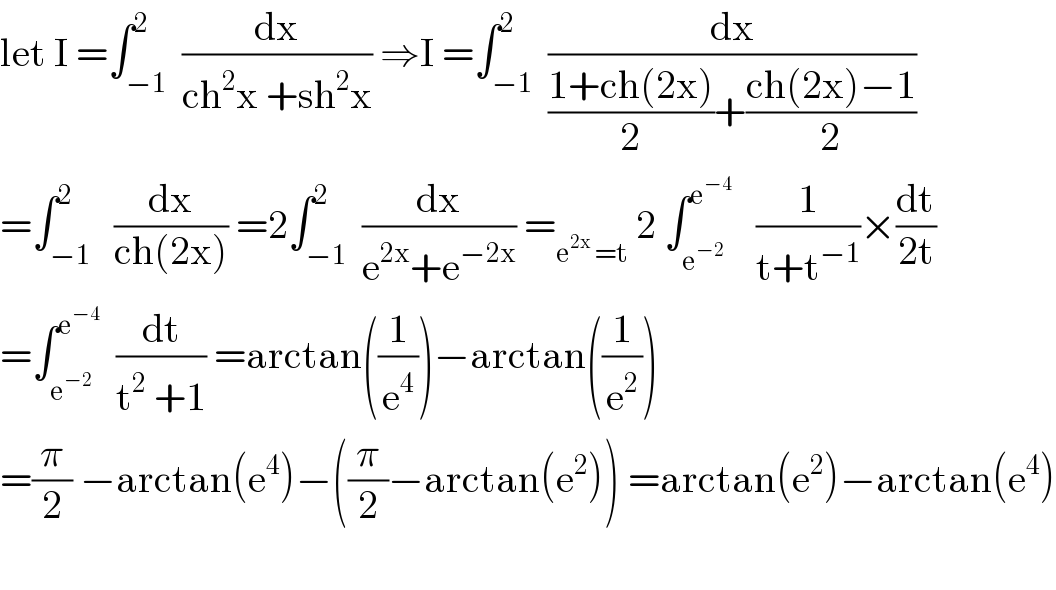
| ||
Question and Answers Forum | ||
Question Number 115366 by Bird last updated on 25/Sep/20 | ||
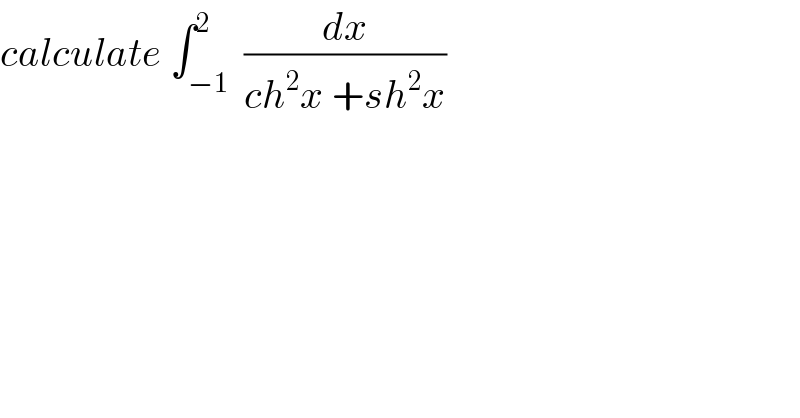 | ||
Answered by MJS_new last updated on 25/Sep/20 | ||
![∫(dx/(cosh^2 x +sinh^2 x))= [t=e^(2x) → dx=(dt/(2e^(2x) ))] =∫(dt/(t^2 +1))=arctan t = =arctan e^(2x) +C ∫_(−1) ^2 (dx/(cosh^2 x +sinh^2 x))=arctan e^4 −arctan e^(−2)](Q115379.png) | ||
| ||
Commented by mathmax by abdo last updated on 25/Sep/20 | ||
 | ||
Answered by mathmax by abdo last updated on 25/Sep/20 | ||
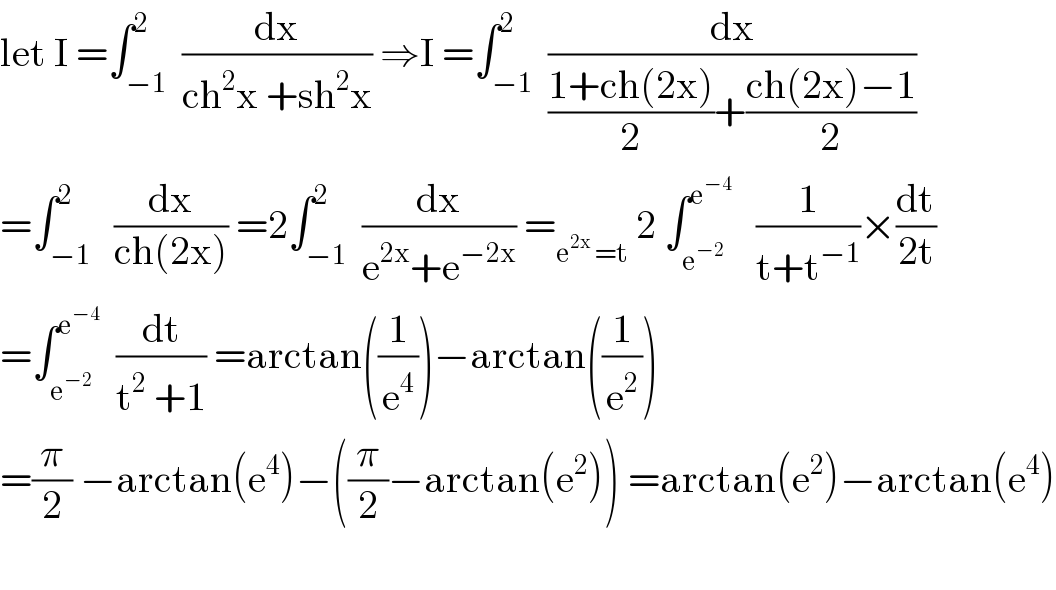 | ||
| ||