
Question and Answers Forum
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 115408 by mr W last updated on 25/Sep/20
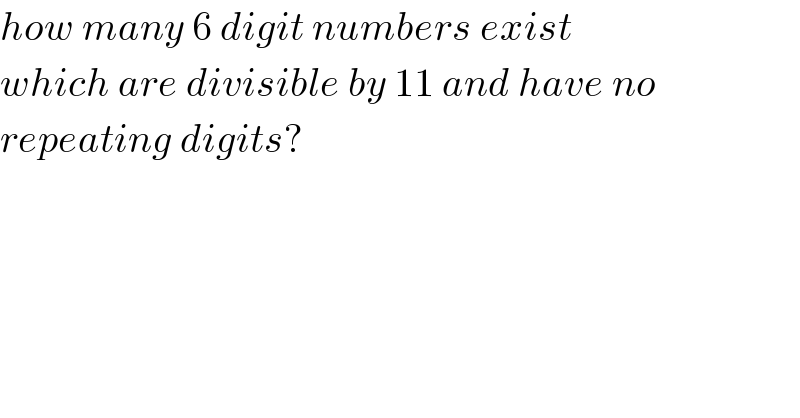
Answered by Olaf last updated on 26/Sep/20
![N = a_5 a_4 a_3 a_2 a_1 a_0 A number is divisible by 11 if the sum of its even−numbered digits substracted from the sum of its odd−numbered digits is zero or a multiple of 11. N = a_0 +10a_1 +10^2 a_2 +10^3 a_3 +10^4 a_4 +10^5 a_5 N = a_0 +(1×11−1)a_1 +(9×11+1)a_2 +(91×11−1)a_3 +(909×11+1)a_4 +(9091×11−1)a_5 ⇒ N = (a_0 −a_1 +a_2 −a_3 +a_4 −a_5 )+11p with p∈Z ⇒ N is divisible by 11 if a_0 −a_1 +a_2 −a_3 +a_4 −a_5 ≡ 0 [11] (a_0 +a_2 +a_4 )−(a_1 +a_3 +a_5 ) ≡ 0 [11] ... to be continued.](Q115458.png)
Commented by mr W last updated on 26/Sep/20

| ||
Question and Answers Forum | ||
Previous in Permutation and Combination Next in Permutation and Combination | ||
Question Number 115408 by mr W last updated on 25/Sep/20 | ||
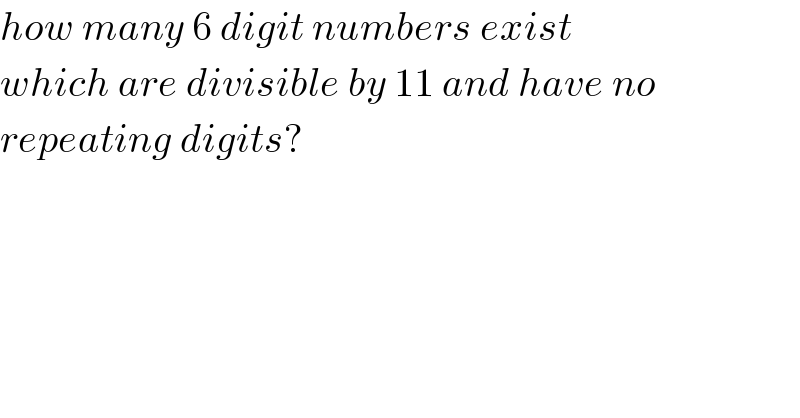 | ||
Answered by Olaf last updated on 26/Sep/20 | ||
![N = a_5 a_4 a_3 a_2 a_1 a_0 A number is divisible by 11 if the sum of its even−numbered digits substracted from the sum of its odd−numbered digits is zero or a multiple of 11. N = a_0 +10a_1 +10^2 a_2 +10^3 a_3 +10^4 a_4 +10^5 a_5 N = a_0 +(1×11−1)a_1 +(9×11+1)a_2 +(91×11−1)a_3 +(909×11+1)a_4 +(9091×11−1)a_5 ⇒ N = (a_0 −a_1 +a_2 −a_3 +a_4 −a_5 )+11p with p∈Z ⇒ N is divisible by 11 if a_0 −a_1 +a_2 −a_3 +a_4 −a_5 ≡ 0 [11] (a_0 +a_2 +a_4 )−(a_1 +a_3 +a_5 ) ≡ 0 [11] ... to be continued.](Q115458.png) | ||
| ||
Commented by mr W last updated on 26/Sep/20 | ||
 | ||