
Question and Answers Forum
Question Number 115459 by john santu last updated on 26/Sep/20
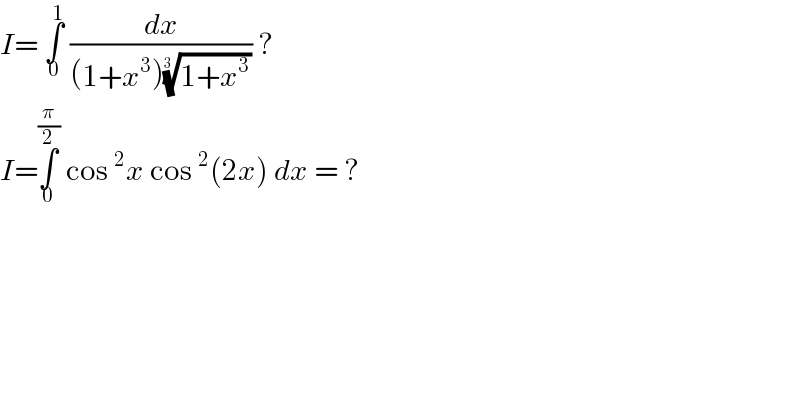
Answered by bemath last updated on 26/Sep/20
![I=∫cos^2 x cos^2 (2x) dx I=∫ (cos x cos (2x))^2 dx I= (1/4)∫ (cos 3x+cos x)^2 dx I=(1/4)∫ (cos^2 (3x)+2cos 3xcos x+cos^2 x)dx I=(1/4)∫((1/2)+(1/2)cos 6x+cos 4x+(3/2)cos 2x+(1/2))dx I=(1/4)∫(1+cos 6x+cos 4x+(3/2)cos 2x)dx I=(1/4)x+(1/(24))sin 6x+(1/(16))sin 4x+(3/(16))sin 2x+c now put border I=∫_0 ^(π/2) cos^2 x cos^2 (2x) dx I= [(x/4) +((sin 6x)/(24)) + ((sin 4x)/(16)) + ((3 sin 2x)/(16)) ]_0 ^(π/2) I=(π/8)](Q115461.png)
Answered by Dwaipayan Shikari last updated on 26/Sep/20
![I=∫_0 ^1 (dx/((1+x^3 )^(4/3) ))=∫_0 ^1 (dx/(x^4 (1+(1/x^3 ))^(4/3) ))=−(1/3)∫_0 ^1 ((((−3)/x^4 )dx)/((1+(1/x^3 ))^(4/3) )) =[(1+(1/x^3 ))^(−(1/3)) ]_0 ^1 =(1/( (2)^(1/3) ))−2](Q115519.png)
Answered by TANMAY PANACEA last updated on 26/Sep/20
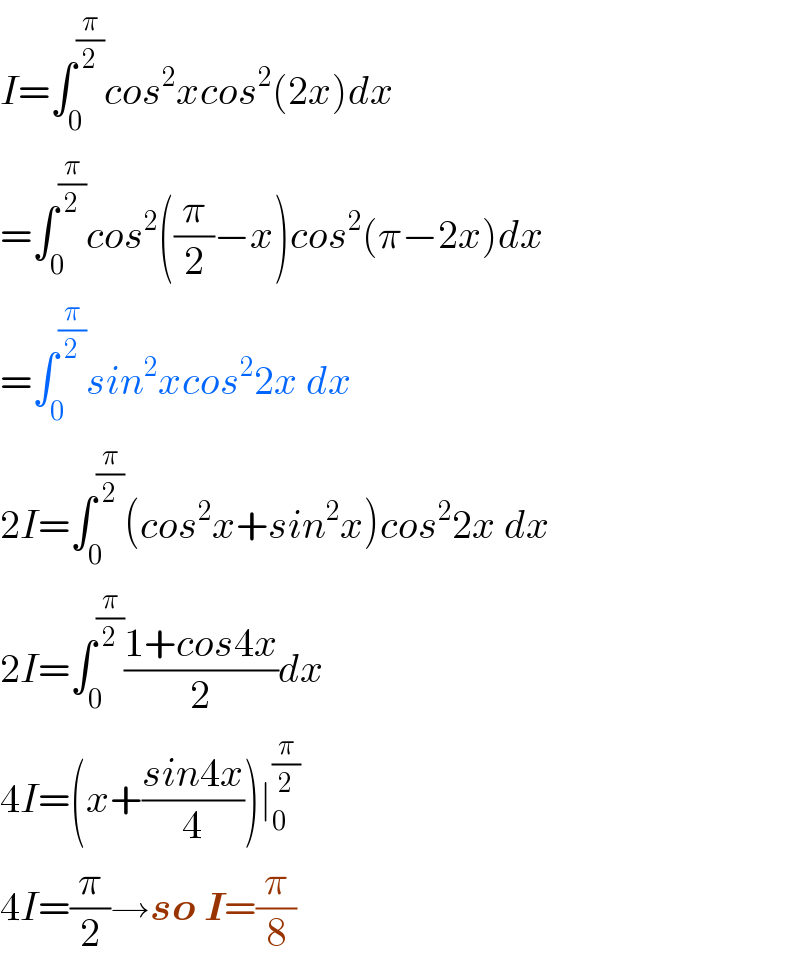
| ||
Question and Answers Forum | ||
Question Number 115459 by john santu last updated on 26/Sep/20 | ||
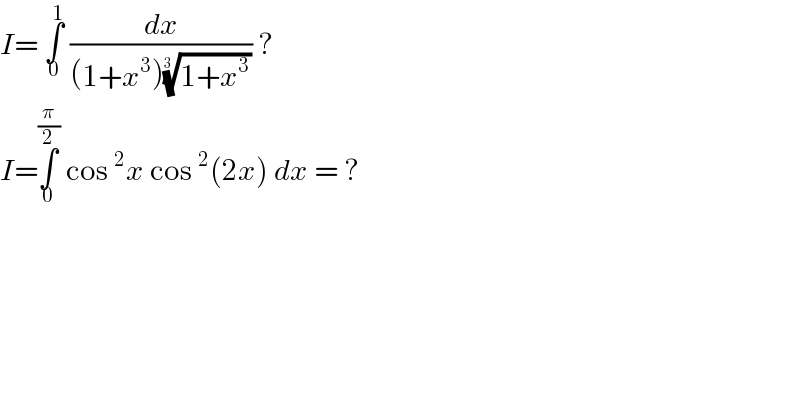 | ||
Answered by bemath last updated on 26/Sep/20 | ||
![I=∫cos^2 x cos^2 (2x) dx I=∫ (cos x cos (2x))^2 dx I= (1/4)∫ (cos 3x+cos x)^2 dx I=(1/4)∫ (cos^2 (3x)+2cos 3xcos x+cos^2 x)dx I=(1/4)∫((1/2)+(1/2)cos 6x+cos 4x+(3/2)cos 2x+(1/2))dx I=(1/4)∫(1+cos 6x+cos 4x+(3/2)cos 2x)dx I=(1/4)x+(1/(24))sin 6x+(1/(16))sin 4x+(3/(16))sin 2x+c now put border I=∫_0 ^(π/2) cos^2 x cos^2 (2x) dx I= [(x/4) +((sin 6x)/(24)) + ((sin 4x)/(16)) + ((3 sin 2x)/(16)) ]_0 ^(π/2) I=(π/8)](Q115461.png) | ||
| ||
Answered by Dwaipayan Shikari last updated on 26/Sep/20 | ||
![I=∫_0 ^1 (dx/((1+x^3 )^(4/3) ))=∫_0 ^1 (dx/(x^4 (1+(1/x^3 ))^(4/3) ))=−(1/3)∫_0 ^1 ((((−3)/x^4 )dx)/((1+(1/x^3 ))^(4/3) )) =[(1+(1/x^3 ))^(−(1/3)) ]_0 ^1 =(1/( (2)^(1/3) ))−2](Q115519.png) | ||
| ||
Answered by TANMAY PANACEA last updated on 26/Sep/20 | ||
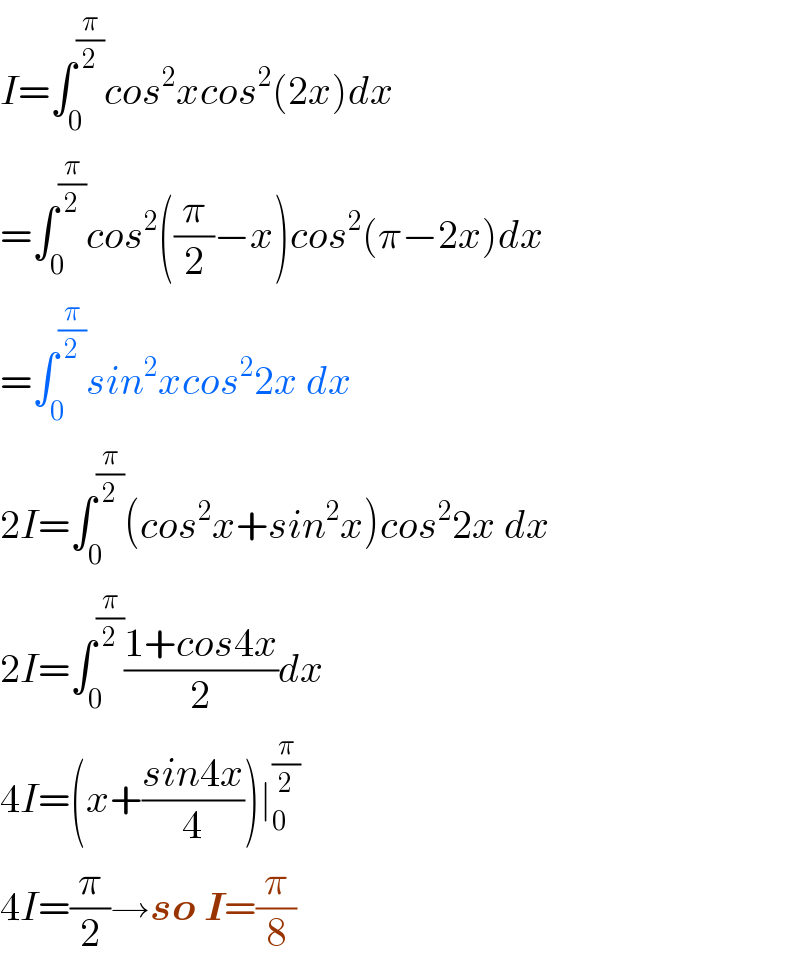 | ||
| ||