Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 115498 by bobhans last updated on 26/Sep/20

$$\int \sec xdx?$$$$\int \sqrt{x-\sqrt{x}}dx?$$$$\underset{n\to \mathrm{\infty }}{\lim }\frac{\left(\sqrt[n]{1+\sqrt{1+n^2}}\right)\left(\sqrt[n]{2+\sqrt{4+n^2}}\right)\left(\sqrt[n]{3+\sqrt{9+n^2}}\right)...\left(\sqrt[n]{n+\sqrt{2n^2}}\right)}{n}?$$

Commented by bobhans last updated on 26/Sep/20

$$thankyouallmaster...$$

Commented by Dwaipayan Shikari last updated on 26/Sep/20

$$\int \sqrt{\mathrm{x}-\sqrt{\mathrm{x}}}\mathrm{dx}\mathrm{x}-\sqrt{\mathrm{x}}=\mathrm{t}\Rightarrow 1-\frac{1}{2\sqrt{\mathrm{x}}}=\frac{\mathrm{dt}}{\mathrm{dx}}$$$$\int \sqrt{{\sin }^4\theta -{\sin }^2\theta }\mathrm{dx}\mathrm{x}=\sin \theta \Rightarrow 1=\cos \theta .\frac{\mathrm{d}\theta }{\mathrm{dx}}$$$$\int \mathrm{icos}\theta \sin \theta \sqrt{1-{\sin }^2\theta }\mathrm{d}\theta$$$$\int {\mathrm{icos}}^2\theta \sin \theta \mathrm{d}\theta$$$$\int {\mathrm{it}}^2.\mathrm{dt}$$$$\mathrm{i}\frac{{\mathrm{t}}^3}{3}+\mathrm{C}=\mathrm{i}\frac{{\cos }^3\theta }{3}+\mathrm{C}=\mathrm{i}\frac{{\cos }^3\left({\sin }^{-1}\mathrm{x}\right)}{3}+\mathrm{C}$$$$\left(\mathrm{Complex}\mathrm{Method}\right)$$

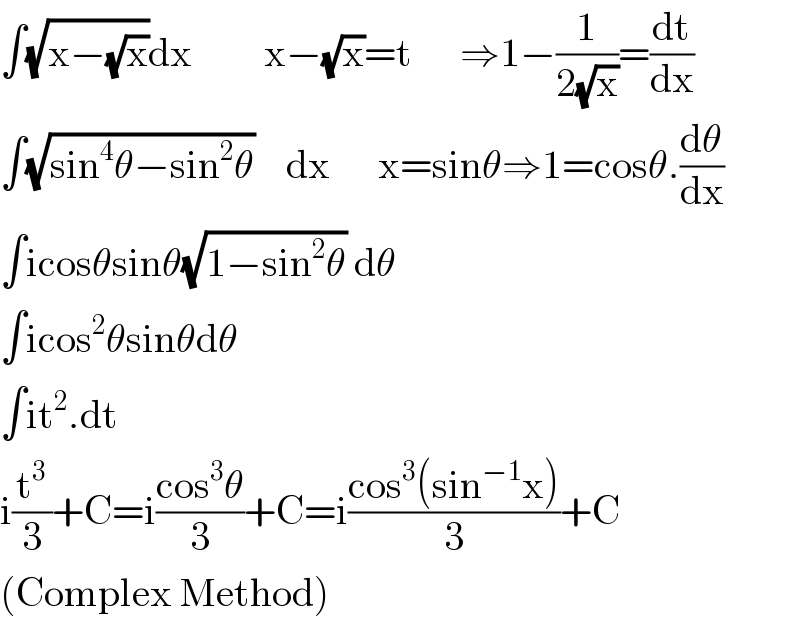
Answered by bemath last updated on 26/Sep/20

$$\left(1\right)\int \frac{dx}{\cos x}=\int \frac{\cos x}{\cos {}^{2}x}dx$$$$\int \frac{d\left(\sin x\right)}{1-\sin {}^{2}x}=\int \frac{dp}{1-p^2}=\tanh {}^{-1}\left(p\right)+c$$$$=\tanh {}^{-1}\left(\sin x\right)+c$$

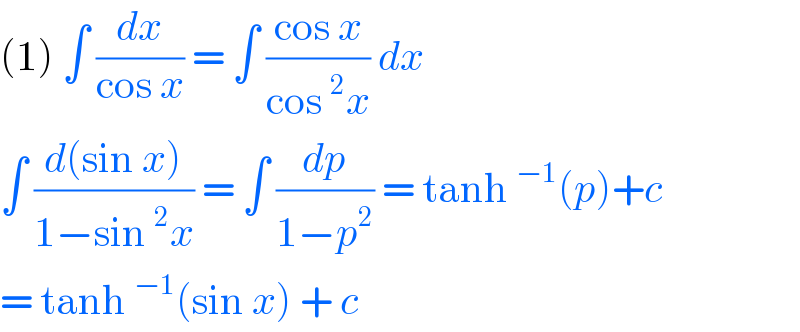
Answered by $@y@m last updated on 26/Sep/20

$$\int \sec xdx$$$$\int \sec x\times \frac{\sec x+\tan x}{\sec x+\tan x}dx$$$$\int \frac{{\sec }^{2}x+\sec x.\tan x}{\sec x+\tan x}dx$$$$\ln (\sec x+\tan x)+\mathrm{C}$$$$$$

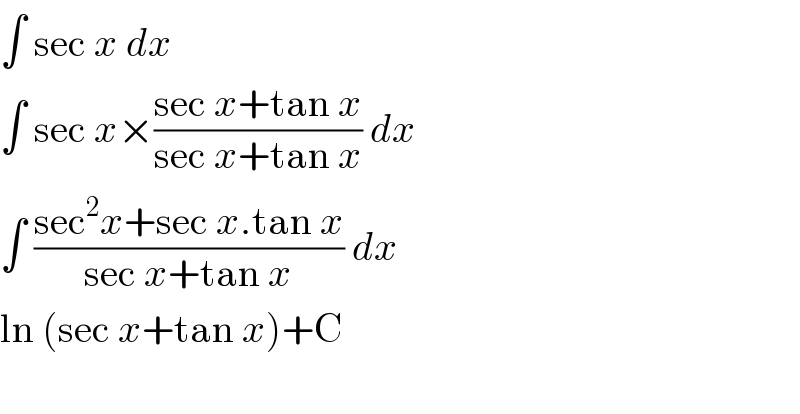
Answered by TANMAY PANACEA last updated on 26/Sep/20

$$\underset{n\to \mathrm{\infty }}{\mathrm{li}m}\frac{\sqrt[n]{1+\sqrt{1^2+n^2}}}{n^{\frac{1}{n}}}\times \frac{\sqrt[n]{2+\sqrt{2^2+n^2}}}{n^{\frac{1}{n}}}\times ..\frac{\sqrt[n]{n+\sqrt{n^2+n^2}}}{n^{\frac{1}{n}}}$$$$lookgeneralterm$$$${\left(\frac{r+\sqrt{r^2+n^2}}{n}\right)}^{\frac{1}{n}}\to {(\frac{r}{n}+\sqrt{1+\frac{r^2}{n^2}})}^{\frac{1}{n}}$$$$ihavedoneerror...socorrectingnow$$$$y=\underset{n\to \mathrm{\infty }}{\lim }\mathrm{\Pi }{(\frac{r}{n}+\sqrt{1+\frac{r^2}{n^2}})}^{\frac{1}{n}}$$$$lny=\underset{n\to \mathrm{\infty }}{\lim }\frac{1}{n}[ln(\frac{1}{n}+\sqrt{1+\frac{1^2}{n^2}})+ln(\frac{2}{n}+\sqrt{1+\frac{2^2}{n^2}})+...ln(\frac{n}{n}+\sqrt{1+\frac{n^2}{n^2}})]$$$$lny={\int }_0^{1}ln(x+\sqrt{1+x^2})dx$$$$$$$$$$$$$$$$$$$$generalterm=\frac{\sqrt[n]{r+\sqrt{r^2+}}}{}$$$$$$

Commented by bemath last updated on 26/Sep/20

$$whythegeneraltermnotcomplete$$

Answered by Dwaipayan Shikari last updated on 26/Sep/20

$$\text{Missing left or extra right}$$$$\frac{1}{\mathrm{n}}\underset{\mathrm{r}=1}{\sum ^{\mathrm{n}}}\log (\frac{\mathrm{r}}{\mathrm{n}}+\sqrt{\frac{{\mathrm{r}}^2}{{\mathrm{n}}^2}+1})=\mathrm{logy}$$$${\int }_0^1\log (\mathrm{x}+\sqrt{{\mathrm{x}}^2+1})\mathrm{dx}$$$${\left[\mathrm{xlog}(\mathrm{x}+\sqrt{{\mathrm{x}}^2+1})\right]}_0^1-{\int }_0^1\frac{\mathrm{x}}{\mathrm{x}+\sqrt{{\mathrm{x}}^2+1}}.(1+\frac{\mathrm{x}}{\sqrt{{\mathrm{x}}^2+1}})\mathrm{dx}$$$$=\log (\sqrt{2}+1)-\frac{1}{2}{\int }_0^1\frac{2\mathrm{x}}{\sqrt{{\mathrm{x}}^2+1}}$$$$=\log (\sqrt{2}+1)-{\left[\sqrt{{\mathrm{x}}^2+1}\right]}_0^1$$$$=\log (\sqrt{2}+1)-\sqrt{2}+1=\mathrm{logy}$$$$\Rightarrow \mathrm{y}=(\sqrt{2}+1){\mathrm{e}}^{1-\sqrt{2}}$$$$$$

Answered by mathmax by abdo last updated on 26/Sep/20

$$\mathrm{let}{\mathrm{U}}_{\mathrm{n}}=\frac{1}{\mathrm{n}}{(1+\sqrt{1+{\mathrm{n}}^2})}^{\frac{1}{\mathrm{n}}}.{\left(\sqrt{2+\sqrt{4+{\mathrm{n}}^2}}\right)}^{\frac{1}{\mathrm{n}}}......{\left(\sqrt{\mathrm{n}+\sqrt{{\mathrm{n}}^2+{\mathrm{n}}^2}}\right)}^{\frac{1}{\mathrm{n}}}$$$$\Rightarrow {\mathrm{U}}_{\mathrm{n}}=\frac{1}{\mathrm{n}}{\left(\prod _{\mathrm{k}=1}^{\mathrm{n}}(\mathrm{k}+\sqrt{{\mathrm{k}}^2+{\mathrm{n}}^2})\right)}^{\frac{1}{\mathrm{n}}}=$$$$=\frac{1}{\mathrm{n}}{\left\{\prod _{\mathrm{k}=1}^{\mathrm{n}}(\mathrm{k}+\mathrm{n}\sqrt{\frac{{\mathrm{k}}^2}{{\mathrm{n}}^2}+1})\right\}}^{\frac{1}{\mathrm{n}}}=\frac{1}{\mathrm{n}}{\left\{{\mathrm{n}}^{\mathrm{n}}\prod _{\mathrm{k}=1}^{\mathrm{n}}(\frac{\mathrm{k}}{\mathrm{n}}+\sqrt{1+{\left(\frac{\mathrm{k}}{\mathrm{n}}\right)}^2})\right\}}^{\frac{1}{\mathrm{n}}}$$$$=(\prod _{\mathrm{k}=1}^{\mathrm{n}}{(\frac{\mathrm{k}}{\mathrm{n}}+\sqrt{1+{\left(\frac{\mathrm{k}}{\mathrm{n}}\right)}^2})}^{\frac{1}{\mathrm{n}}}\Rightarrow \ln \left({\mathrm{U}}_{\mathrm{n}}\right)=\frac{1}{\mathrm{n}}\sum _{\mathrm{k}=1}^{\mathrm{n}}\ln (\frac{\mathrm{k}}{\mathrm{n}}+\sqrt{1+{\left(\frac{\mathrm{k}}{\mathrm{n}}\right)}^2})$$$$\Rightarrow {\lim }_{\mathrm{n}\to +\mathrm{\infty }}\ln \left({\mathrm{U}}_{\mathrm{n}}\right)={\int }_0^1\ln (\mathrm{x}+\sqrt{1+{\mathrm{x}}^2})\mathrm{dx}\mathrm{we}\mathrm{have}$$$${\int }_0^1\ln (\mathrm{x}+\sqrt{1+{\mathrm{x}}^2})\mathrm{dx}={\left[\mathrm{xln}(\mathrm{x}+\sqrt{1+{\mathrm{x}}^2})\right]}_0^1-{\int }_0^1\mathrm{x}.\frac{\mathrm{dx}}{\sqrt{1+{\mathrm{x}}^2}}$$$$=\ln (1+\sqrt{2})-{\left[\sqrt{1+{\mathrm{x}}^2}\right]}_0^1=\ln (1+\sqrt{2})-(\sqrt{2}-1)$$$$\Rightarrow {\lim }_{\mathrm{n}\to +\mathrm{\infty }}{\mathrm{U}}_{\mathrm{n}}={\mathrm{e}}^{\ln (1+\sqrt{2})+1-\sqrt{2}}=(1+\sqrt{2}){\mathrm{e}}^{1-\sqrt{2}}=\mathrm{S}$$$$$$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com