Question and Answers Forum
Question Number 115507 by mnjuly1970 last updated on 26/Sep/20
![.... ...matematical analysis... prove that ::: a>0 :: [((i : ∫_(0 ) ^( ∞) ((sin^2 (ax))/x^(3/2) ) dx= (√(πa)))),((ii: ∫_0 ^( ∞) ((sin^3 (ax))/( (√x))) dx = ((−1+3(√(3 )))/4) (√((π/(6a)) )) )) ] ...m.n.july.1970...](Q115507.png)
Answered by mathdave last updated on 26/Sep/20

Commented bymnjuly1970 last updated on 26/Sep/20
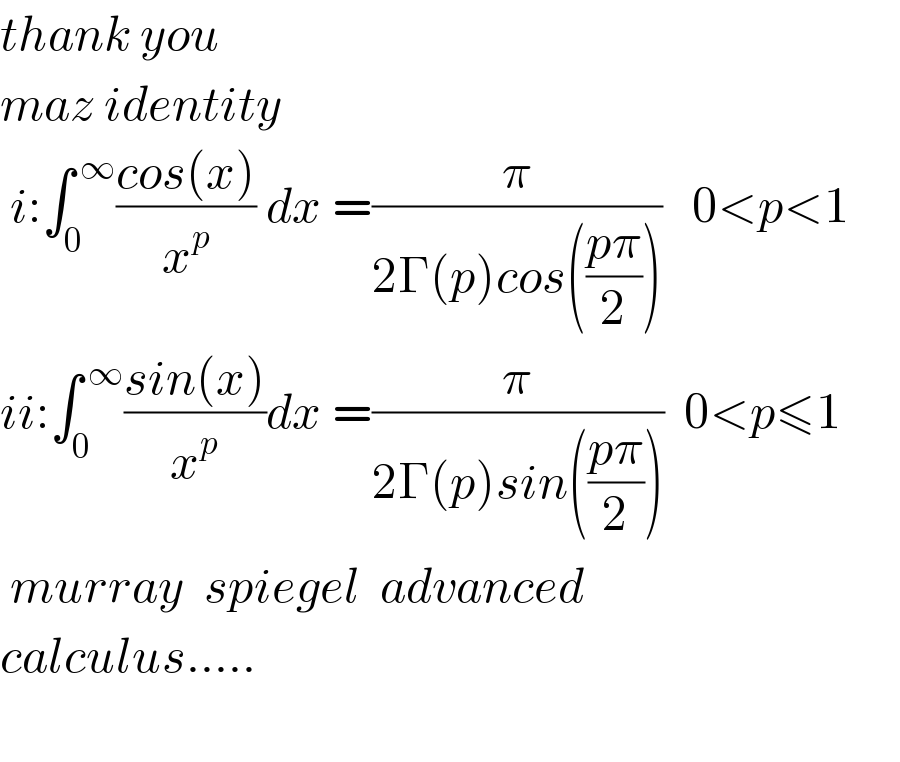
Commented bymnjuly1970 last updated on 26/Sep/20
Answered by Bird last updated on 28/Sep/20
![I=∫_0 ^∞ ((sin^2 (ax))/x^(3/2) ) dx ⇒I =_(ax =t) ∫_0 ^∞ ((sin^2 t)/(((t/a))^(3/2) ))×(dt/a) =a^((3/2)−1) ∫_0 ^∞ ((sin^2 t)/t^(3/2) )dt ==(√(a ))∫_0 ^∞ ((sin^2 t )/t^(3/2) )dt by parts ∫_0 ^∞ t^(−(3/(2 ))) sin^2 t dt =[(1/(1−(3/2))) t^(1−(3/2)) sin^2 t]_0 ^∞ −∫_0 ^∞ −2 t^(−(1/2)) ×2sint cost dt =2 ∫_0 ^∞ ((sin(2t))/( (√t))) dt =_((√t)=u) 2∫_0 ^∞ ((sin(2u^2 ))/u)(2u)du =4 ∫_0 ^∞ sin(2u^2 )du =−4 Im(∫_0 ^∞ e^(−2iu^2 ) du) ∫_0 ^∞ e^(−((√(2i))u)^2 ) du =_((√(2i))u=z) ∫_0 ^∞ e^(−z^2 ) (dz/( (√(2i)))) =(1/( (√2)))e^(−((iπ)/4)) ×((√π)/2) =((√π)/(2(√2)))(((√2)/2)−((i(√2))/2)) =((√π)/4)−((i(√π))/4) ⇒ ∫_0 ^∞ t^(−(3/2)) sin^2 t dt =−4(−((√π)/4))=(√π) ⇒I =(√a)×(√π) =(√(πa))](Q115724.png)
Commented bymnjuly1970 last updated on 28/Sep/20